熵
最大熵模型
最大熵模型(Maximum Entropy Model,以下简称MaxEnt),MaxEnt 是概率模型学习中一个准则,其思想为:在学习概率模型时,所有可能的模型中熵最大的模型是最好的模型;若概率模型需要满足一些约束,则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。
最大熵原理指出,对一个随机事件的概率分布进行预测时,预测应当满足全部已知的约束,而对未知的情况不要做任何主观假设。在这种情况下,概率分布最均匀,预测的风险最小,因此得到的概率分布的熵是最大。
关于条件分布$P(X|Y)$的熵为:
$H(P) =–\sum_{x,y}P(y,x)logP(y|x)= –\sum_{x,y}\widetilde{P}(x)P(y|x)logP(y|x)$
首先满足约束条件然后使得该熵最大即可,MaxEnt 模型$P^*$为
$P^* = arg\max_{P \in C} H(P) \ \ 或 \ \ P^* = arg\min_{P \in C} -H(P)$
综上给出形式化的最大熵模型:
给定数据集$\left \{ (x_i,y_i)\right\}_{i=1}^N$,特征函数$f_i(x,y),i= 1,2…,n$,根据经验分布得到满足约束集的模型集合C
$\begin{aligned} & \min_{P \in C} \ \ \sum_{x,y} \widetilde{P}(x)P(y|x)logP(y|x) \\ & \ s.t. \ \ \ E_p(f_i) = E _{\widetilde{P}}(f_i) \\ & \ \ \ \ \ \ \ \ \ \sum_yP(y|x) = 1 \end{aligned}$
简单粗暴的说:逻辑回归跟最大熵模型没有本质区别。逻辑回归是最大熵对应为二类时的特殊情况,也就是说,当逻辑回归扩展为多类别的时候,就是最大熵模型。
信息熵
信息熵是度量随机变量不确定度的指标,信息熵越大意味着随机变量不确定度越高,意味着系统的有序程度越低。他的定义
如果随机变量$P=\{x_1,x_2,...,x_n\}$,他的概率$P\{P=x_i\},i\in \{1,2,..,n\}$,则随机变量$P=\{x_1,x_2,...,x_n\}$的熵定义为
$H( P)=-\sum_{i=1}^n p(x_i)log_2 p(x_i)$
交叉熵
$H\left(P,Q\right)=-\sum_{i=1}^n p(x_i)log_2 q(x_i)$
交叉熵刻画的是两个概率分布的距离,也就是说交叉熵越小,两个概率分布越接近
交叉熵可在神经网络(机器学习)中作为损失函数,p表示真实标记的分布,q则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
相对熵
考虑某个未知的分布 p(x) ,假定我们已经使用一个近似的分布 q(x) 对它进行了建模。如果我们使用 q(x) 来建立一个编码体系,用来把 x 的值传给接收者,那么,由于我们使用了 q(x) 而不是真实分布 p(x) ,因此在具体化 x 的值(假定我们选择了一个高效的编码系统)时,我们需要一些附加的信息。我们需要的平均的附加信息量(单位是 nat )为
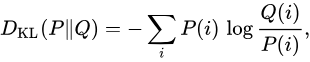
其又被称为KL散度(Kullback–Leibler divergence,KLD) Kullback–Leibler divergence。
KL散度计算的就是数据的原分布与近似分布的概率的对数差的期望值。
同时,从这可以看出,只有p(x)的积分是一个定值,所以比较不相似度时也可以去掉第二项,就发现第一项其实就是交叉熵!交叉熵实际上是更广泛的相对熵的特殊情形。
就是2个函数或概率分布的差异性:差异越大则相对熵越大,差异越小则相对熵越小,特别地,若2者相同则熵为0。
注意,KL散度的非对称性。这意味着D(P||Q) ≠ D(Q||P)。
用处:在聚类算法中,使用相对熵代替欧几里得距离,计算连个节点的相关度,据说效果不错。度量两个随机变量的差异性。
这幅图就是说,p分布和q分布共有的部分相对熵就是正的,非共有部分就是负的,D(p||q)就是面积的求和。
条件熵
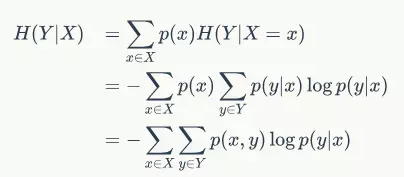
注意,这个条件熵,不是指在给定某个数(某个变量为某个值)的情况下,另一个变量的熵是多少,变量的不确定性是多少,而是期望!
因为条件熵中X也是一个变量,意思是在一个变量X的条件下(变量X的每个值都会取),另一个变量Y熵对X的期望。
通俗来讲就是,知道X情况下,Y的信息量。
性质:
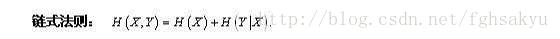
**用处:决策树的特征选择,实际上使用的信息增益,就是用G(D,A)=H(Y)-H(Y|X)。可以看出在X的条件下,Y的不确定度下降了多少。
互信息(mutual information)
如果 (X, Y) ~ p(x, y), X, Y 之间的互信息 I(X; Y)定义为:
Note: 互信息 I (X; Y)可为正、负或0。
互信息实际上是更广泛的相对熵的特殊情形
如果变量不是独立的,那么我们可以通过考察联合概率分布与边缘概率分布乘积之间的 KL散度来判断它们是否“接近”于相互独立。此时, KL散度为
这被称为变量 x 和变量 y 之间的互信息( mutual information )。根据 KL散度的性质,我们看到 I[x, y] ≥ 0 ,当且仅当 x 和 y 相互独立时等号成立。
使用概率的加和规则和乘积规则,我们看到互信息和条件熵之间的关系为
可以把互信息看成由于知道 y 值而造成的 x 的不确定性的减小(反之亦然)(即Y的值透露了多少关于X 的信息量)。


互信息、条件熵与联合熵的区别与联系
venn图表示关系

由于 H(X|X) = 0, 所以, H(X) = H(X) – H(X|X) = I(X; X)
这一方面说明了为什么熵又称自信息,另一方面说明了两个完全相互依赖的变量之间的互信息并不是一个常量,而是取决于它们的熵。
从图中可以看出,条件熵可以通过联合熵 - 熵( H(X|Y) = H(X, Y) - H(Y) )表示,也可以通过熵 - 互信息( H(X|Y) = H(X) - I(X; Y) )表示。




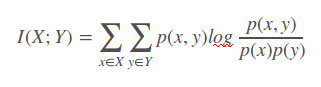
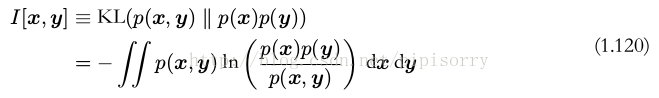
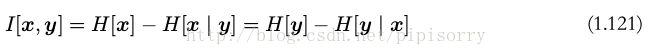

 浙公网安备 33010602011771号
浙公网安备 33010602011771号