随机森林

概述

鉴于决策树容易过拟合的缺点，随机森林采用多个决策树的投票机制来改善决策树，我们假设随机森林使用了m棵决策树，那么就需要产生m个一定数量的样本集来训练每一棵树，如果用全样本去训练m棵决策树显然是不可取的，全样本训练忽视了局部样本的规律，对于模型的泛化能力是有害的

产生n个样本的方法采用Bootstrap法，这是一种有放回的抽样方法，产生n个样本

而最终结果采用Bagging的策略来获得，即多数投票机制

Random Forest算法的优点主要有三个。

第一，不同决策树可以由不同主机并行训练生成，效率很高；

第二，随机森林算法继承了CART的优点；

第三，将所有的决策树通过bagging的形式结合起来，避免了单个决策树造成过拟合的问题。 

优点

1、 在当前的很多数据集上，相对其他算法有着很大的优势，表现良好

2、它能够处理很高维度（feature很多）的数据，并且不用做特征选择

        PS：特征子集是随机选择的

3、在训练完后，它能够给出哪些feature比较重要

        PS：http://blog.csdn.net/keepreder/article/details/47277517

4、在创建随机森林的时候，对generlization error使用的是无偏估计，模型泛化能力强

5、训练速度快，容易做成并行化方法

       PS：训练时树与树之间是相互独立的

6、 在训练过程中，能够检测到feature间的互相影响

7、 实现比较简单

8、 对于不平衡的数据集来说，它可以平衡误差。

9、如果有很大一部分的特征遗失，仍可以维持准确度。

 

缺点：

  1. 随机森林在解决回归问题时，并没有像它在分类中表现的那么好，这是因为它并不能给出一个连续的输出。当进行回归时，随机森林不能够做出超越训练集数据范围的预测，这可能导致在某些特定噪声的数据进行建模时出现过度拟合。（PS:随机森林已经被证明在某些噪音较大的分类或者回归问题上回过拟合）。
  2. 对于许多统计建模者来说，随机森林给人的感觉就像一个黑盒子，你无法控制模型内部的运行。只能在不同的参数和随机种子之间进行尝试。
  3. 可能有很多相似的决策树，掩盖了真实的结果。
  4. 对于小数据或者低维数据（特征较少的数据），可能不能产生很好的分类。（处理高维数据，处理特征遗失数据，处理不平衡数据是随机森林的长处）。
  5. 执行数据虽然比boosting等快（随机森林属于bagging），但比单只决策树慢多了。

基础知识

Bootstrap: 名字来自成语“pull up by your own bootstraps”，意思是依靠你自己的资源，称为自助法，它是一种有放回的抽样方法，它是非参数统计中一种重要的估计统计量方差进而进行区间估计的统计方法。其核心思想和基本步骤如下：
　　（1） 采用重抽样技术从原始样本中抽取一定数量（自己给定）的样本，此过程允许重复抽样。
　　（2） 根据抽出的样本计算给定的统计量T。 
　　（3） 重复上述N次（一般大于1000），得到N个统计量T。 
　　（4） 计算上述N个统计量T的样本方差，得到统计量的方差。
　　应该说Bootstrap是现代统计学较为流行的一种统计方法，在小样本时效果很好。通过方差的估计可以构造置信区间等，其运用范围得到进一步延伸。

 

cart树介绍：

机器学习之分类与回归树(CART)

Bagging（套袋法）

bagging的算法过程如下：

  1. 从原始样本集中使用Bootstraping方法随机抽取n个训练样本，共进行k轮抽取，得到k个训练集。（k个训练集之间相互独立，元素可以有重复）
  2. 对于k个训练集，我们训练k个模型（这k个模型可以根据具体问题而定，比如决策树，knn等）
  3. 对于分类问题：由投票表决产生分类结果；对于回归问题：由k个模型预测结果的均值作为最后预测结果。（所有模型的重要性相同）

 

随机森林的生成方法：

先假设我们有N个样本，M个特征，那么在这种情况下我们是如何构建随机森林的：

a、构建一棵树，我们利用自助法（bootstrap）从N个样本中选取N个样本，需要注意的是，这N个样本是大概率会有重复的，选取的这N个样本就是根节点待分裂的样本；

b、在每个待分裂节点上，我们从M个特征中随机选取m个特征（<<M，通常是log2或sqrt的数量），从这m个属性中根据某种策略（分类：如gini减少或信息增益等 回归：找到使得切分之后的方差最小）确定分裂属性；

c、重复b步骤，直到不能分裂或达到我们设定的阈值（如叶子节点数或树的深度），此时建立了一颗决策树；

d、重复上面的a、b、c步骤，直到达到预定树的棵数T为止。

最后，如果是分类算法预测，则T个弱学习器投出最多票数的类别或者类别之一为最终类别。

如果是回归算法，T个弱学习器得到的回归结果进行算术平均得到的值为最终的模型输出。

回归确定分裂属性的方法：

遍历变量j，对规定的切分变量j扫描切分点s，选择使下式得到最小值时的(j,s)对。其中Rm是被划分的输入空间，cm是空间Rm对应的固定输出值。

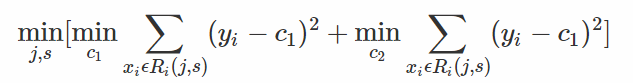
随机森林每个分裂点都是随机选取m个特征，需要注意的是：在随机森林中不是每棵树随机选择一批特征来分裂，而是在每个节点上都是随机选取的。

 

 随机性：

1.Bootstraping方法随机抽取n个训练样本

2.随机抽取一部分特征

例如，原来有100个特征，现在只从中随机选取30个来构成决策树，那么每一轮得到的树都由不同的30个特征构成，每棵树都不一样。假设原来样本维度是d，则只选择其中的d’（d’小于d）个维度来建立决策树结构。这类似是一种从d维到d’维的特征转换，相当于是从高维到低维的投影，也就是说d’维z空间其实就是d维x空间的一个随机子空间（subspace）。通常情况下，d’远小于d，从而保证算法更有效率。Random Forest算法的作者建议在构建C&RT每个分支b(x)的时候，都可以重新选择子特征来训练，从而得到更具有多样性的决策树。

3.还可以将现有的特征x，通过数组p进行线性组合，来保持多样性：

\phi_i(x)=p_i^Tx

这种方法使每次分支得到的不再是单一的子特征集合，而是子特征的线性组合（权重不为1）。好比在二维平面上不止得到水平线和垂直线，也能得到各种斜线。这种做法使子特征选择更加多样性。值得注意的是，不同分支i下的 p_i 是不同的，而且向量 p_i 中大部分元素为零，因为我们选择的只是一部分特征，这是一种低维映射。

 

所以，这里的Random Forest算法又有增强，由原来的random-subspace变成了random-combination。顺便提一下，这里的random-combination类似于perceptron模型。

 

 

为什么绝大多数随机森林算法中用的都是cart树

在sklearn中的随机森林算法中用的就是cart树，在分类问题中，分裂方式不限于gini，也可以选entropy，在回归问题中，用的是mse和mae。

ID3有很多明显不足的地方：比如不能处理连续性变量；不能处理缺失值；选择分裂变量时会倾向于选择类别较多的变量（理解这个问题可以想的极端一点，如ID类的特征，每一类下都只有一个输出项）；容易过拟合。

同样，C4.5也有一些问题：C4.5生成的是多叉树，即一个父节点可以有多个节点。很多时候，在计算机中二叉树模型会比多叉树运算效率高，如果采用二叉树，可以提高效率；C4.5只能用于分类，不能用于回归；C4.5由于使用了熵模型，里面有大量耗时的对数运算,如果是连续值还有大量的排序运算，运算效率较低。

cart树可以分类可以回归。

cart树里面引入了一个gini系数的概念，gini的计算相比熵要简单的多，所以可以减少一定的运算量。

cart树第二个特点在于节点的分裂上，每次节点分裂都是二叉的，所以cart树就是多个二叉树组成的，这种特点使得cart算法与C4.5算法在处理离散变量上有很大的不同，离散变量在C4.5中只有一次可能出现在分裂节点上，分裂的枝数与离散变量的类别数量有关。

因为每次都是二分裂，所以cart也没有ID3中倾向于选择类别较多的变量的缺陷。

cart树对连续变量的处理与C4.5类似。

台大林轩田机器学习技法（十）：随机森林

上一部分我们已经介绍了Random Forest算法，而Random Forest算法重要的一点就是Bagging。

接下来将继续探讨bagging中的bootstrap机制到底蕴含了哪些可以为我们所用的东西。

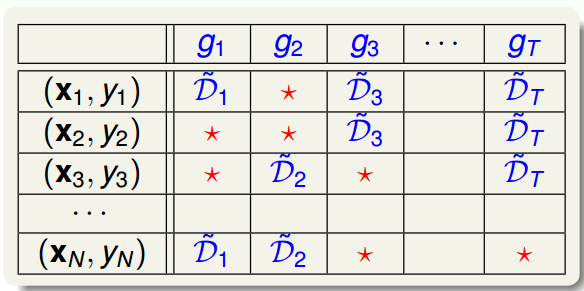
不同的验证集：Out-Of-Bag Estimate

通过bootstrap得到新的样本集D’，再由D’训练不同的 g_t 。我们知道D’中包含了原样本集D中的一些样本，但也有些样本没有涵盖进去。如下表所示，不同的 g_t 下，红色的*表示在 \hat D_t 中没有这些样本。例如对 g_1 来说， (x_2,y_2) 和 (x_3,y_4) 没有包含进去，对 g_2 来说， (x_1,y_1) 和 (x_2,y_2) 没有包含进去，等等。每个 g_t 中，红色表示的样本被称为out-of-bag(OOB) example。

 

首先，我们来计算OOB样本到底有多少。假设bootstrap的数量N’=N，那么某个样本 (x_n,y_n) 是OOB的概率是：

(1-\frac1N)^N=\frac{1}{(\frac{N}{N-1})^N}=\frac{1}{(1+\frac{1}{N-1})^N}\approx \frac1e

其中，e是自然对数，N是原样本集的数量。由上述推导可得，每个 g_t 中，OOB数目大约是 \frac1eN ，即大约有三分之一的样本没有在bootstrap中被抽到。

然后，我们将OOB与之前介绍的Validation进行对比：

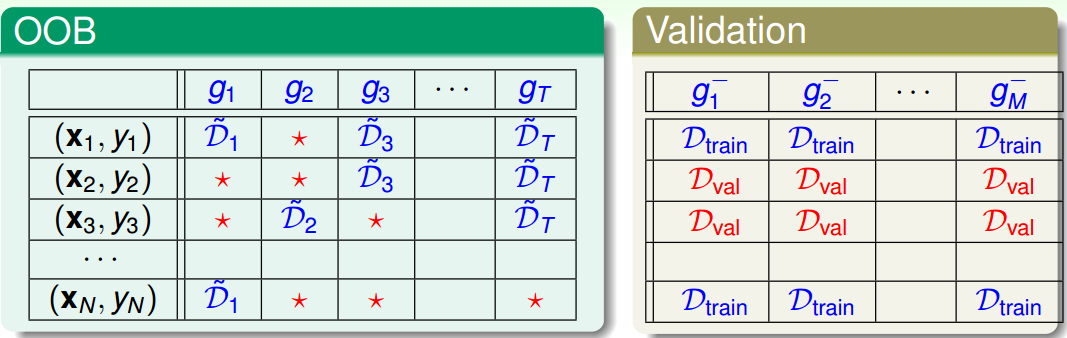
在Validation表格中，蓝色的 D_{train} 用来得到不同的 g_m^- ，而红色的 D_{val} 用来验证各自的 g_m^- 。 D_{train} 与 D_{val} 没有交集，一般 D_{train} 是 D_{val} 的数倍关系。再看左边的OOB表格，之前我们也介绍过，蓝色的部分用来得到不同的 g_t ，而红色的部分是OOB样本。而我们刚刚也推导过，红色部分大约占N的 \frac1e 。通过两个表格的比较，我们发现OOB样本类似于 D_{val} ，那么是否能使用OOB样本来验证 g_t 的好坏呢？答案是肯定的。但是，通常我们并不需要对单个 g_t 进行验证。因为我们更关心的是由许多 g_t 组合成的G，即使 g_t 表现不太好，只要G表现足够好就行了。那么问题就转化成了如何使用OOB来验证G的好坏。方法是先看每一个样本 (x_n,y_n) 是哪些 g_t 的OOB资料，然后计算其在这些 g_t 上的表现，最后将所有样本的表现求平均即可。例如，样本 (x_N,y_N) 是 g_2 ， g_3 ， g_T 的OOB，则可以计算 (x_N,y_N) 在 G_N^-(x) 上的表现为：

G_N^-(x)=average(g_2,g_3,g_T)

这种做法我们并不陌生，就像是我们之前介绍过的Leave-One-Out Cross Validation，每次只对一个样本进行 g^- 的验证一样，只不过这里选择的是每个样本是哪些 g_t 的OOB，然后再分别进行 G_n^-(x) 的验证。每个样本都当成验证资料一次（与留一法相同），最后计算所有样本的平均表现：

E_{oob}(G)=\frac1N\sum_{n=1}^Nerr(y_n,G_n^-(x_n))

E_{oob}(G) 估算的就是G的表现好坏。我们把 E_{oob} 称为bagging或者Random Forest的self-validation。

这种self-validation相比于validation来说还有一个优点就是它不需要重复训练。如下图左边所示，在通过 D_{val} 选择到表现最好的 g_{m^*}^- 之后，还需要在 D_{train} 和 D_{val} 组成的所有样本集D上重新对该模型 g_{m^*}^- 训练一次，以得到最终的模型系数。但是self-validation在调整随机森林算法相关系数并得到最小的 E_{oob} 之后，就完成了整个模型的建立，无需重新训练模型。随机森林算法中，self-validation在衡量G的表现上通常相当准确。

 

随机森林用于特征选择

如果样本资料特征过多，假如有10000个特征，而我们只想从中选取300个特征，这时候就需要舍弃部分特征。通常来说，需要移除的特征分为两类：一类是冗余特征，即特征出现重复，例如“年龄”和“生日”；另一类是不相关特征，例如疾病预测的时候引入的“保险状况”。这种从d维特征到d’维特征的subset-transform \Phi(x) 称为Feature Selection，最终使用这些d’维的特征进行模型训练。

 

 

特征选择的优点是：

  • 提高效率，特征越少，模型越简单
  • 正则化，防止特征过多出现过拟合
  • 去除无关特征，保留相关性大的特征，解释性强

同时，特征选择的缺点是：

  • 筛选特征的计算量较大
  • 不同特征组合，也容易发生过拟合
  • 容易选到无关特征，解释性差

 

值得一提的是，在decision tree中，我们使用的decision stump切割方式也是一种feature selection。

那么，如何对许多维特征进行筛选呢？我们可以通过计算出每个特征的重要性（即权重），然后再根据重要性的排序进行选择即可。

这种方法在线性模型中比较容易计算。因为线性模型的score是由每个特征经过加权求和而得到的，而加权系数的绝对值 |w_i| 正好代表了对应特征 x_i 的重要性为多少。 |w_i| 越大，表示对应特征 x_i 越重要，则该特征应该被选择。w的值可以通过对已有的数据集 (x_i,y_i) 建立线性模型而得到。

 

然而，对于非线性模型来说，因为不同特征可能是非线性交叉在一起的，所以计算每个特征的重要性就变得比较复杂和困难。例如，Random Forest就是一个非线性模型，接下来，我们将讨论如何在RF下进行特征选择。

RF中，特征选择的核心思想是random test。random test的做法是对于某个特征，如果用另外一个随机值替代它之后的表现比之前更差，则表明该特征比较重要，所占的权重应该较大，不能用一个随机值替代。相反，如果随机值替代后的表现没有太大差别，则表明该特征不那么重要，可有可无。所以，通过比较某特征被随机值替代前后的表现，就能推断出该特征的权重和重要性。

那么random test中的随机值如何选择呢？通常有两种方法：

一是使用uniform或者gaussian抽取随机值替换原特征；二是通过permutation的方式将原来的所有N个样本的第i个特征值重新打乱分布（相当于重新洗牌）。

比较而言，第二种方法更加科学，保证了特征替代值与原特征的分布是近似的（只是重新洗牌而已）。

这种方法叫做permutation test（随机排序测试），即在计算第i个特征的重要性的时候，将N个样本的第i个特征重新洗牌，然后比较D和 D^{(p)} 表现的差异性。如果差异很大，则表明第i个特征是重要的。

知道了permutation test的原理后，接下来要考虑的问题是如何衡量上图中的performance，即替换前后的表现。显然，我们前面介绍过performance可以用 E_{oob}(G) 来衡量。但是，对于N个样本的第i个特征值重新洗牌重置的 D^{(p)} ，要对它进行重新训练，而且每个特征都要重复训练，然后再与原D的表现进行比较，过程非常繁琐。为了简化运算，RF的作者提出了一种方法，就是把permutation的操作从原来的training上移到了OOB validation上去，记为 E_{oob}(G^{(p)})\rightarrow E_{oob}^{(p)}(G) 。也就是说，在训练的时候仍然使用D，但是在OOB验证的时候，将所有的OOB样本的第i个特征重新洗牌，验证G的表现。这种做法大大简化了计算复杂度，在RF的feature selection中应用广泛。

 

posted @ 2018-05-10 10:28  喵喵帕斯  阅读(3050)  评论(0)  编辑  收藏  举报