python numpy
0.axis的意义
Pandas保持了Numpy对关键字axis的用法,用法在Numpy库的词汇表当中有过解释:
轴用来为超过一维的数组定义的属性,二维数据拥有两个轴:第0轴沿着行的垂直往下,第1轴沿着列的方向水平延伸。
如果简单点来说,就是0轴匹配的是index, 涉及上下运算;1轴匹配的是columns, 涉及左右运算。
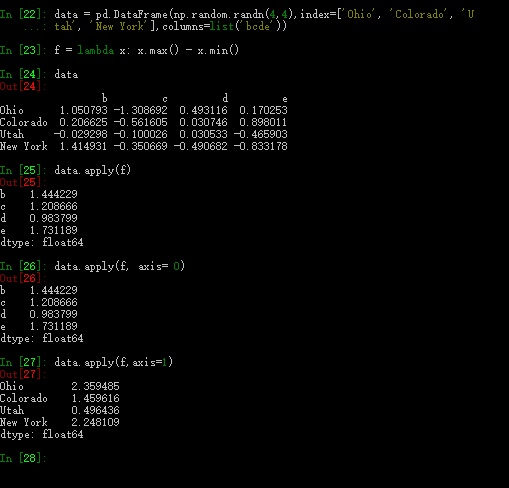
https://www.zhihu.com/question/58993137
1.numpy.random.randn
numpy.random.randn(d0, d1, ..., dn)
d0, d1, …, dn:应该为正整数,表示维度。
如果没有参数,则返回一个值,如果有参数,则返回(d0, d1, …, dn)个值,这些值都是从标准正态分布中随机取样得到的。
For random samples from , use:
sigma * np.random.randn(...) + mu
2.numpy.random.rand
numpy.random.rand(d0, d1, ..., dn)
d0, d1, ..., dn :返回数组的尺寸,都应该是正的。
创建一个给定类型的数组,将其填充在一个均匀分布的随机样本[0, 1)中
3.numpy.reshape
Gives a new shape to an array without changing its data.
>>> a = np.array([[1,2,3], [4,5,6]])
>>> np.reshape(a, 6)
array([1, 2, 3, 4, 5, 6])
>>> np.reshape(a, (3,-1)) # the unspecified value is inferred to be 2
array([[1, 2],
[3, 4],
[5, 6]])
4.shape函数
shape函数是numpy.core.fromnumeric中的函数,它的功能是查看矩阵或者数组的维数。
>>> e = eye(3) >>> e array([[ 1., 0., 0.], [ 0., 1., 0.], [ 0., 0., 1.]]) >>> e.shape (3, 3)
建立一个4×2的矩阵c, c.shape[1] 为第一维的长度,c.shape[0] 为第二维的长度。
>>> c = array([[1,1],[1,2],[1,3],[1,4]]) >>> c.shape (4, 2) >>> c.shape[0] 4 >>> c.shape[1] 2
5.numpy.zeros
用法:zeros(shape, dtype=float, order='C')
返回:返回来一个给定形状和类型的用0填充的数组;
参数:shape:形状
dtype:数据类型,可选参数,默认numpy.float64
dtype类型:t ,位域,如t4代表4位
b,布尔值,true or false
i,整数,如i8(64位)
u,无符号整数,u8(64位)
f,浮点数,f8(64位)
c,浮点负数,
o,对象,
s,a,字符串,s24
u,unicode,u24
order:可选参数,c代表与c语言类似,行优先;F代表列优先
例子:
np.zeros(5)
array([ 0., 0., 0., 0., 0.])
s = (2,2)
np.zeros(s)
array([[ 0., 0.],
[ 0., 0.]])
6.argsort()
1.先定义一个array数据
import numpy as np x=np.array([1,4,3,-1,6,9])
2.现在我们可以看看argsort()函数的具体功能是什么:
x.argsort()
输出定义为y=array([3,0,2,1,4,5])。
我们发现argsort()函数是将x中的元素从小到大排列,提取其对应的index(索引),然后输出到y。
3.由于在程序中遇到了类似于np.argsort()[num]的形式,一直看不明白,就自己去python环境自己试了下:
ps:这里的num的绝对值小于等于x中元素的个数
当num>=0时,np.argsort()[num]就可以理解为y[num];
当num<0时,np.argsort()[num]就是把数组y的元素反向输出,例如np.argsort()[-1]即输出x中最大值对应的index,np.argsort()[-2]即输出x中第二大值对应的index,依此类推。。
直观的实验才能看到效果,下面是我拿上面例子做的验证:

这是当num为负值时的输出。

这个是num>=0时的输出。
7.dot()
dot()函数是矩阵乘,而*则表示逐个元素相乘
8.random.choice()
可以从一个int数字或1维array里随机选取内容,并将选取结果放入n维array中返回。
numpy.random.choice(a, size=None, replace=True, p=None)
a : 1-D array-like or int If an ndarray, a random sample is generated from its elements. If an int, the random sample is generated as if a was np.arange(n)
size : int or tuple of ints, optional
replace : boolean, optional Whether the sample is with or without replacement
p : 1-D array-like, optional The probabilities associated with each entry in a. If not given the sample assumes a uniform distribution over all entries in a.
9.numpy.flatnonzero():
该函数输入一个矩阵,返回扁平化后矩阵中非零元素的位置(index)
这是官方文档给出的用法,非常正规,输入一个矩阵,返回了其中非零元素的位置
>>> x = np.arange(-2, 3) >>> x array([-2, -1, 0, 1, 2]) >>> np.flatnonzero(x) array([0, 1, 3, 4])
用来返回某个特定元素的位置:
对向量元素的判断d==3返回了一个和向量等长的由0/1组成的矩阵,然后调用函数,返回的位置,就是对应要找的元素的位置。
d = np.array([1,2,3,4,4,3,5,3,6]) haa = np.flatnonzero(d == 3) print haa
10.numpy.bincount
计数非负整数数组中每个值的出现次数。
bin的数量比数组中的最大值大1,每个bin给出了它的索引值在数组中出现的次数。
# 我们可以看到x中最大的数为7,因此bin的数量为8,那么它的索引值为0->7 x = np.array([0, 1, 1, 3, 2, 1, 7]) # 索引0出现了1次,索引1出现了3次......索引5出现了0次...... np.bincount(x) #因此,输出结果为:array([1, 3, 1, 1, 0, 0, 0, 1]) # 我们可以看到x中最大的数为7,因此bin的数量为8,那么它的索引值为0->7 x = np.array([7, 6, 2, 1, 4]) # 索引0出现了0次,索引1出现了1次......索引5出现了0次...... np.bincount(x) #输出结果为:array([0, 1, 1, 0, 1, 0, 1, 1])
11.np.linspace
linspace可以用来实现相同间隔的采样。
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
返回值为numpy.ndarray。
linspace(a,b,c)均匀生成介于a到b的c个值,c默认为100
如linspace(0,100,5)即[0 25 50 75 100]
linspace(-1.3,1.3)就是生成介于-1.3到1.3的100个值
12.meshgrid
meshgrid是生成网格的函数,一般是生成二维网格矩阵数据,但这里生成的是三维网格矩阵数据。
先以二维数据为例,
比如要绘制函数z=f(x,y)的图像
x方向在[1,2,3,4,5]五个点上采样,即x=1:5
y方向在[10 20 30 40]四个点上采样,即y=10:10:40
那么就一共有5*4=20个采样点。
分别为
(1,10) (2,10) (3,10) (4,10) (5,10)
(1,20) (2,20) (3,20) (4,20) (5,20)
(1,30) (2,30) (3,30) (4,30) (5,30)
(1,40) (2,40) (3,40) (4,40) (5,40)
命令
[X,Y]=meshgrid(x,y)
生成的X就是这20个采样点的横坐标,Y既是其纵坐标,即
X=
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
Y=
10 10 10 10 10
20 20 20 20 20
30 30 30 30 30
40 40 40 40 40
然后再对这20个采样点计算z的值,即Z=f(X,Y),最后用mesh(X,Y,Z)即可绘制图像
三维网格数据与此类似,现在xyz三个方向都是取-1.3到1.3的100个数据,总共就是100^3即一百万个采样点,[x,y,z]=meshgrid(linspace(-1.3,1.3));中的x,y和z就分别是这一百万个采样点的三个维度上的坐标。
13.concatenate()
numpy.concatenate((a1, a2, ...), axis=0)
a1, a2, ... : 需要拼接的矩阵
axis : 沿着某个轴拼接,默认为列方向
举个例子:
In [1]: import numpy as np
In [2]: a = np.array([[1,2,3],[4,5,6]])
In [3]: b = np.zeros((3,3))
In [4]: c = np.ones((4,3))
In [5]: d = np.concatenate((a,b,c))
In [6]: print d
输出结果:
[[ 1. 2. 3.]
[ 4. 5. 6.]
[ 0. 0. 0.]
[ 0. 0. 0.]
[ 0. 0. 0.]
[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]
14.np.mean
求行或列的平均值
axis=0 求列的平均值
axis=1 求行的平均值
>>> a = np.array([[1, 2], [3, 4]]) >>> np.mean(a) 2.5 >>> np.mean(a, axis=0) array([ 2., 3.]) >>> np.mean(a, axis=1) array([ 1.5, 3.5])
answer=np.array([1, 0, 1, 1, 1, 1]) y=np.array([0, 0, 0, 0, 0, 1]) print(answer==y)
结果: [False True False False False True]
answer=np.array([1, 0, 1, 1, 1, 1]) y=np.array([0, 0, 0, 0, 0, 1]) print(np.mean(answer == y[test])) 结果: 0.333333333333
说明:
1、 answer == y表示两个数组中的值相同时,输出True;否则输出False
2、例3对例2中结果取平均值,其中True=1,False=0;
15.Python numpy函数hstack() vstack() stack() dstack() vsplit() concatenate()
16.np.copy
numpy关于copy有三种情况,完全不复制、视图(view)或者叫浅复制(shadow copy)和深复制(deep copy)。
而 b = a[:] 这种形式就属于第二种,即视图,这本质上是一种切片操作(slicing),所有的切片操作返回的都是视图。具体来说,b = a[:]会创建一个新的对象 b(所以 id(b) 和id(a) 返回的结果是不一样的),但是 b 的数据完全来自于a,和 a 保持完全一致,换句话说,b的数据完全由a保管,他们两个的数据变化是一致的,可以看下面的示例:
a = np.arange(4) # array([0, 1, 2, 3]) b = a[:] # array([0, 1, 2, 3]) b.flags.owndata # 返回 False,b 并不保管数据 a.flags.owndata # 返回 True,数据由 a 保管 # 改变 a 同时也影响到 b a[-1] = 10 # array([0, 1, 2, 10]) b # array([0, 1, 2, 10]) # 改变 b 同时也影响到 a b[0] = 10 # array([10, 1, 2, 10]) a # array([10, 1, 2, 10])
b = a 和 b = a[:] 的差别就在于后者会创建新的对象,前者不会。两种方式都会导致 a 和 b 的数据相互影响。
要想不让 a 的改动影响到 b,可以使用深复制:
unique_b = a.copy()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号