数据结构知识点 编程
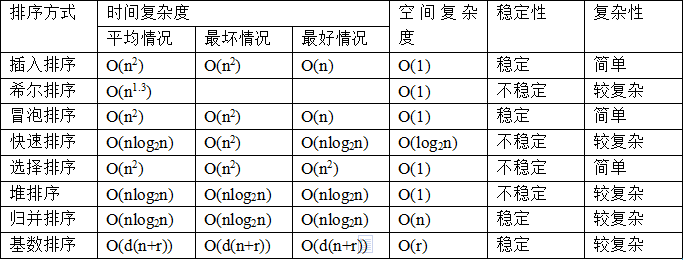
排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
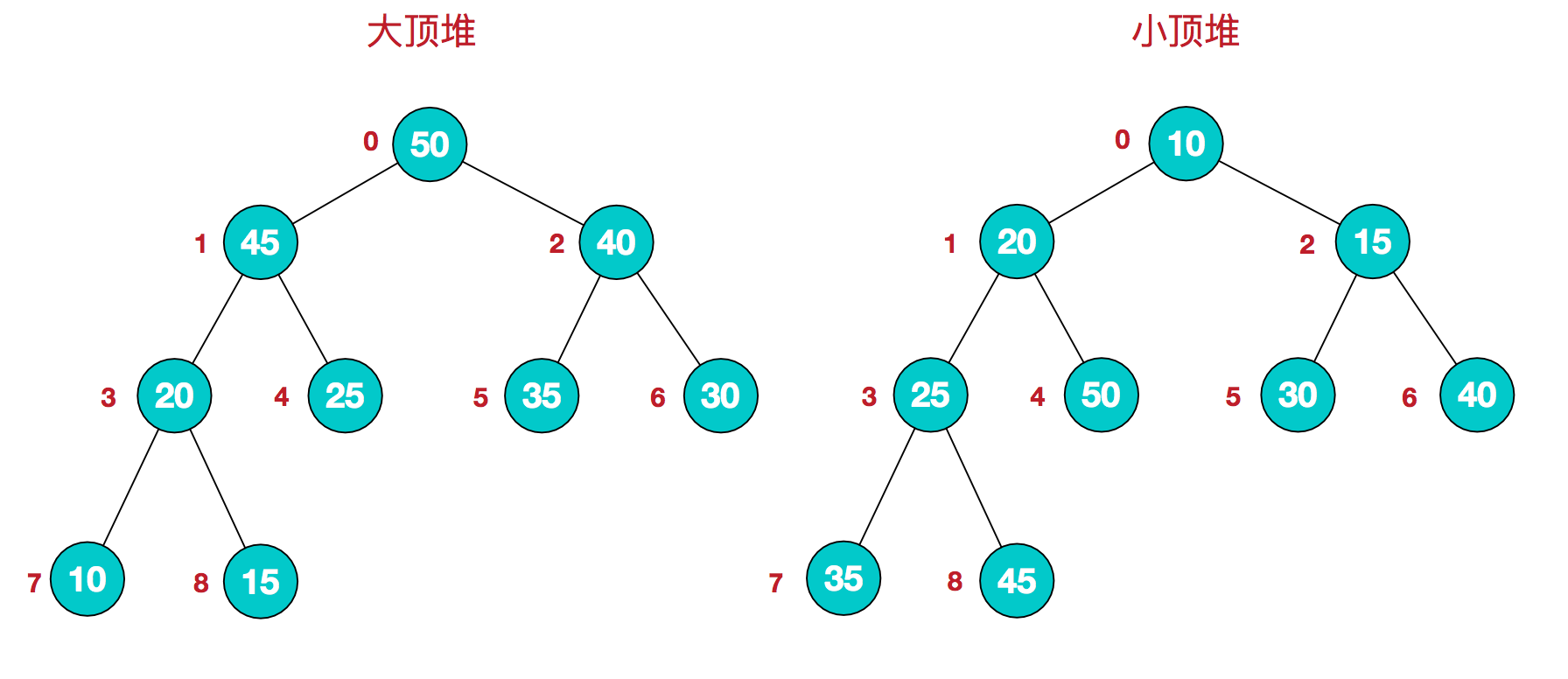
同时,我们对堆中的结点按层进行编号,将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构,我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
第一个非叶子结点 arr.length/2-1
堆排序的基本思路:
a.将无序序列构建成一个堆,根据升序降序需求选择大顶堆(升序)或小顶堆;
最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1),从下至上,从右至左进行调整
升序:
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
排序算法(三)堆排序原理与实现(小顶堆)
void AdjustDown(int arr[], int i, int n) { int j = i * 2 + 1;//子节点 while (j<n) { if (j+1<n && arr[j] > arr[j + 1])//子节点中找较小的 { j++; } if (arr[i] < arr[j]) { break; } swap(arr[i],arr[j]); i = j; j = i * 2 + 1; } } void MakeHeap(int arr[], int n)//建堆 { int i = 0; for (i = n / 2 - 1; i >= 0; i--)//((n-1)*2)+1 =n/2-1 { AdjustDown(arr, i, n); } } void HeapSort(int arr[],int len) { int i = 0; MakeHeap(arr, len); for (i = len - 1; i >= 0; i--) { swap(arr[i], arr[0]); AdjustDown(arr, 0, i); } }
冒泡排序
/* * 冒泡排序 */ public class BubbleSort { public static void main(String[] args) { int[] arr={6,3,8,2,9,1}; System.out.println("排序前数组为:"); for(int num:arr){ System.out.print(num+" "); } for(int i=0;i<arr.length-1;i++){//外层循环控制排序趟数 for(int j=0;j<arr.length-1-i;j++){//内层循环控制每一趟排序多少次 if(arr[j]>arr[j+1]){ int temp=arr[j]; arr[j]=arr[j+1]; arr[j+1]=temp; } } } System.out.println(); System.out.println("排序后的数组为:"); for(int num:arr){ System.out.print(num+" "); } } }
归并排序
public static int[] sort(int[] a,int low,int high){ int mid = (low+high)/2; if(low<high){ sort(a,low,mid); sort(a,mid+1,high); //左右归并 merge(a,low,mid,high); } return a; } public static void merge(int[] a, int low, int mid, int high) { int[] temp = new int[high-low+1]; int i= low; int j = mid+1; int k=0; // 把较小的数先移到新数组中 while(i<=mid && j<=high){ if(a[i]<a[j]){ temp[k++] = a[i++]; }else{ temp[k++] = a[j++]; } } // 把左边剩余的数移入数组 while(i<=mid){ temp[k++] = a[i++]; } // 把右边边剩余的数移入数组 while(j<=high){ temp[k++] = a[j++]; } // 把新数组中的数覆盖nums数组 for(int x=0;x<temp.length;x++){ a[x+low] = temp[x]; } }
快速排序
// 快速排序 static void quickSort(int left, int right, int[] nums) { if (left < right) { int pivot = nums[left]; int low = left; int high = right; while (low < high) { while (low < high && nums[high] >= pivot) { high--; } if (nums[high] < pivot) nums[low] = nums[high]; while (low < high && nums[low] <= pivot) { low++; } if (nums[low] > pivot) nums[high] = nums[low]; } nums[low] = pivot; quickSort(left, low - 1, nums); quickSort(low + 1, right, nums); } }
选择排序
a) 原理:每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕。也就是:每一趟在n-i+1(i=1,2,…n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。基于此思想的算法主要有简单选择排序、树型选择排序和堆排序。(这里只介绍常用的简单选择排序)
b) 简单选择排序的基本思想:给定数组:int[] arr={里面n个数据};第1趟排序,在待排序数据arr[1]~arr[n]中选出最小的数据,将它与arrr[1]交换;第2趟,在待排序数据arr[2]~arr[n]中选出最小的数据,将它与r[2]交换;以此类推,第i趟在待排序数据arr[i]~arr[n]中选出最小的数据,将它与r[i]交换,直到全部排序完成。
public class Selection { public static void sort(int[] arr){ for(int i=0; i<arr.length-1; i++) { int minPos = i; for (int j = i; j < arr.length; j++) { if (arr[j] < arr[minPos]) { minPos = j;//找出当前最小元素的位置 } } if(arr[minPos]!=arr[i]) { swap(arr,minPos,i); } } } public static void swap(int[] arr,int a,int b){ int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; } }
衍生算法:
双向选择排序(每次循环,同时选出最大值放在末尾,最小值放在前方)。
public class Selection { public static void doubleSort(int[] arr){ for(int i=0; i<arr.length/2-1; i++) { int minPos = i,maxPos = arr.length -i -1; for (int j = i; j < arr.length -i; j++) { if (arr[j] < arr[minPos]) { minPos = j; } if(arr[maxPos] <arr[j]){ maxPos = j; } } if(i!=minPos) { swap(arr,i,minPos);//(1) } if(maxPos!=arr.length - i - 1) { if (maxPos == i){//若当前最大值在循环起始位置,则最大值一定在(1)处被交换到了minPos的位置 maxPos = minPos; } swap(arr,maxPos,arr.length -i -1); } } } public static void swap(int[] arr,int a,int b){ int temp = arr[a]; arr[a] = arr[b]; arr[b] = temp; } }
插入排序:
从第二个元素开始,将当前元素插入到前面对应位置,使当前元素i
和之前元素形成有序数组。
比较规则:
正常:
从第一个元素开始,若当前元素i小于有序数组中的元素j,则从该元素开始将有序数组依次后移一位,
并将当前元素i放置到该元素j位置。(插入)
public class Insertion { public static void sort(int[] arr){ int pos,temp; for(int i=1;i<arr.length;i++){ pos = i; while(pos!=0&&arr[pos]<arr[pos-1]){ temp = arr[pos]; arr[pos] = arr[pos-1]; arr[pos-1] = temp; pos--; } } } }
有图片:
三种基础排序算法(选择排序、插入排序、冒泡排序)
为什么先序遍历和后序遍历不能确定唯一的二叉树
前序和后序在本质上都是将父节点与子结点进行分离,但并没有指明左子树和右子树的能力,因此得到这两个序列只能明确父子关系,而不能确定一个二叉树。
由二叉树的中序和前序遍历序列可以唯一确定一棵二叉树 ,由前序和后序遍历则不能唯一确定一棵二叉树
顺序表 线性表 数组的区别
-
数组就是相同数据类型的元素按一定顺序排列的集合。
一句话:就是物理上存储在一组联系的地址上。也称为数据结构中的物理结构。
-
线性表中数据元素之间的关系是一对一的关系,即除了第一个和最后一个数据元素之外,其它数据元素都是首尾相接的。
一句话:线性表是数据结构中的逻辑结构。可以存储在数组上,也可以存储在链表上。
-
线性表的结点按逻辑次序依次存放在一组地址连续的存储单元里的方法。用顺序存储方法存储的线性表简称为顺序表。
一句话:用数组来存储的线性表就是顺序表。
对一个无向图进行先深搜索时,得到的先深序列是唯一的 X
哈希法的平均查找长度不随表中结点数目的增加而增加,而是随负载因子的增大而增大
采用哈希表组织100万条记录,以支持字段A快速查找
理论上可以在常数时间内找到特定记录
所有记录必须存在内存中
拉链式哈希曼最坏查找时间复杂度是O(n)
哈希函数的选择跟A无关
答案:C
A,记录共有100万条,一般的哈希表长度不可能做这么长,因此要解决散列冲突问题,因此一般不能再常数时间内找到记录
B,哈希查找可以在外存中查找,可以用哈希表映射到文件,分级查找
C,最坏情况是所有记录的散列值都冲突,这样就退化为线性查找,时间复杂度为O(n)
D,哈希函数的选择跟A关系密切,跟A的字段类型有关,哈希函数设计的好坏也影响着查找的速度
二叉树在线索化后,仍不能有效求解的问题是后序线索二叉树中求后序后继
前序遍历(中左右)、中序遍历(左中右)的最后访问的节点都是左或右叶节点, 叶节点是没有子树的,所以两个指针域空出来了,可以存放线索指针。但是后续遍历(左右中), 最后访问的子树的根节点,子树根节点的两个指针域都指向子树了,所以不能空出来存放线索信息。
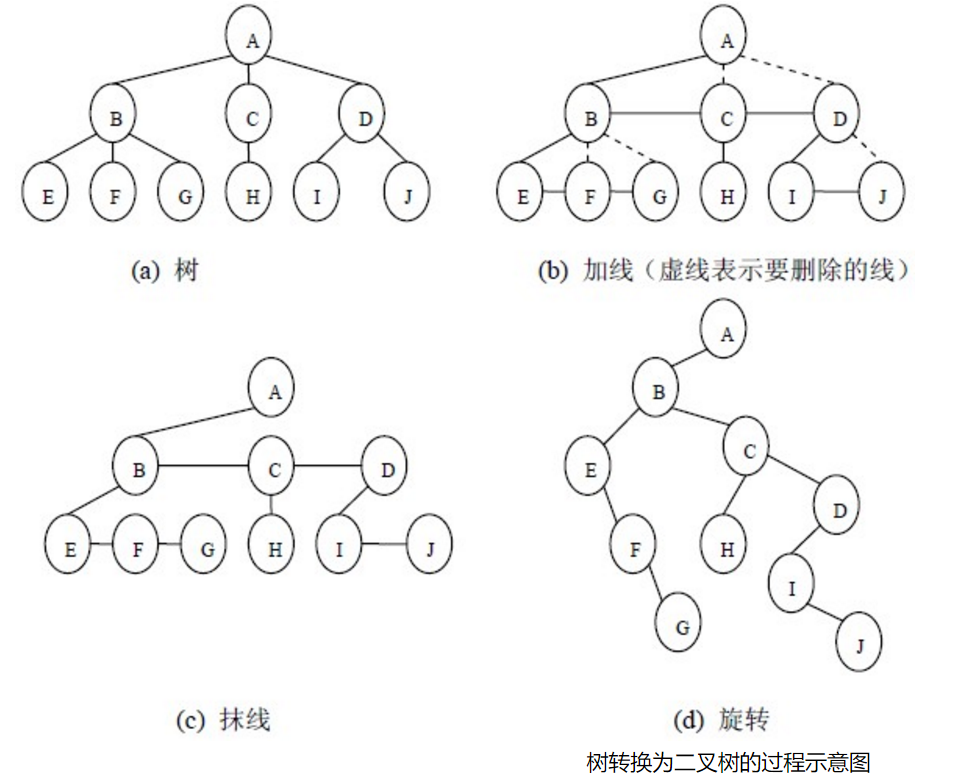
把一棵树转换为二叉树后,这棵二叉树的形态是唯一的
若一个有向图的邻接矩阵对角线以下元素均为零,则该图的拓扑有序序列必定存在
一个有向图能被拓扑排序的充要条件就是它是一个有向无环图。
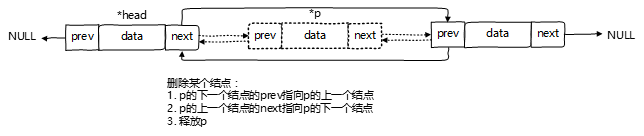
双链表中至多只有一个结点的后继指针为空
强连通分量是无向图的极大强连通子图
有向图强 连通分量 :在 有向图 G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点 强连通 (strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个 强连通图 。有向图的极大强连通子图,称为强连通 分量 (strongly connected components)。
如果约定树中结点的度数不超过2,则它实际上就是一棵二叉树 X
因为已经说是树了,所以不考虑回路的问题,其次二叉树度为2,子树有左右之分,次序不能颠倒。因此仅仅说度不超过2不能说是一颗二叉树。
外部排序思想
现在我要进行排序,不过需要排序的数据很大,有1000G那么大,但是我的机器内存只有2G大小,所以每次只能把2G的数据从文件中传入内存,然后用一个“内部排序“算法在内存排好序后,再将这有序数据,载入一个2G大小的文件。然后再载入第二个2G数据。。。循环500遍之后,我现在得到500个文件,每个文件2G,文件内部是有序的,然后我再比较这500个文件的第一个数,最小的肯定就是这1000G数据的最小的。那么之后的过程你肯能想到了,就是不断将这500个2G 数据进行一个归并,最终就能得到这1000G的有序数据文件了。
举个例子,比如我要排序10个数,但是我的内存一次只能装下5个数,所以最初的10个数我只能放到文件里面(文件时外存,只要硬盘或磁盘够大,想多大就多大)。内部排序肯定是得需要将数据载入内存中才可以进行的。
这10个数是[ 2 ,3,1,7,9 ,6, 8,4 ,5 ,0 ]。
第一次载入前五个数2,3,1,7,9. 排好序后是:1,2,3,7,9 然后导入一个只存五个数的文件中。
第二次载入后五个数6,8,4,5,0 排好序后是:0,4,5,6,8,然后倒入一个只存五个数的文件中。
之后在归并两个有序数列
第一个有序子数列的头位1,第二个为0,因为0然后在进行第二次比较,1和4进行比较。。。
重复进行最终得到一个有序数列的文件,里面存着,0,1,2,3,,,7,8,9
问题是:在这个过程中,你能想到哪些优化?
(擦,,,背景描述了半天,问题就一句话。。。当时我也很无语。。。)
解答:
想了大概一分钟,除了增设一个缓冲buffer,加速从文件到内存的转储之外,我脑子里面一片空空。。。而且我想到的那个缓冲buffer所得到的回复是“假设这个优化系统已经帮你优化了” 。。。无语。。。
他看我眉头紧锁,然后给我做了一个提示:假设我现在把文件中的2G数据载入内存这个过程定义为”L”,把内存中的排序过程定义为”S” ,把排序好的 2G数据再转储到另一个文件这个过程定义为”T”…
他还没说完,瞬间反应过来了!“用流水线并行实现“,然后我把流水线那个图画了出来,就是在计算机组成原理那本书中经常出现的“流水线图”。图画好后,他点点头,我也长嘘一口气。。。
然后他问我,用流水线技术之后为什么会加速整个过程。
当然这个问题就很容易了,过去得把一组2G数据的三个过程全部处理完之后,才能进行下一个2G数据的处理,现在就可以三个过程并行着进行了。当时我也忘了,加速比怎么计算了,所以就没提这个东西。。。
他接着问,做了这个并行处理之后,会出现什么问题?
。。。MD,又是一个恶心问题,其实我清楚,问题不难,但是“找问题”好讨厌啊。。。
想了一下,我说,在“S”这个过程,也就是内部排序的这个环节最好不要用“快速排序”,因为快速排序是不稳定的排序,所以在流水线那个图中会出现不均匀的时间块,影响整体性能。
他想了一下,点点头。问,还有吗?给你个提示吧,你想想加了这个优化之后,某个资源会不会出问题?
我想了想,“资源”,计算机的资源没几样啊,CPU,内存。。。再一次,瞬间恍然大明白,是内存出的问题,因为,如果并行进行的话,打个比方,比如现在同时处理的过程是,第一个2G数据的“T”阶段(因为第一个2G数据,比较早的进入流水线,所以之前的两个阶段已经处理完毕),第二个2G数据的“S”阶段,第三个2G数据的“L”阶段,那么这三个阶段是都需要把数据放到内存中的,所以一共得需要6G内存,但是目前计算机的实际内存只有2G啊!!!
解决方法很简单,将内存平均分为三份,分别用于处理三个阶段的数据。
这样带来的影响是,现在一次就不能处理2G数据了,只能处理2/3G的数据,流水线会加长。
他看这块处理的差不多了,就继续提示,你看看在最后的归并上有什么优化?
最后的归并就是不断在一组有序数列中找最小值,还用刚才那个例子,最后不是得到500个2G有序数列吗,但是扫描每个文件头,找最小值,最差情形要比较500次,平均复杂度是O(n),n为最后得到的有序数组的个数,此例子为500。
他既然问有没有什么优化?那么必然是存在logn的算法了。一提logn和最小值,那没的说,必须是“堆”啊!!!
然后我给他说了一下具体实现细节
就是维护一个大小为n的“最小堆”,每次返回堆顶元素,就为当前所有文件头数值的那个最小值。然后根据刚才弹出的那个最小值是属于哪个文件的,然后再将那个文件此时的头文件所指向的数,插入到最小堆中,文件指针自动后移。插入过程为logn复杂度,但是每次返回最小值的复杂度为O(1),运行时空间复杂度为O(n)。 OK,搞定。
下面的排序方法中,关键字比较次数与记录的初始排列无关的是:
堆排序和选择排序的排序次数与初始状态无关,即最好情况和最坏情况都一样
堆排序平均执行的时间复杂度和需要附加的存储空间复杂度分别是O(Nlog2N)和O(1)
下列选项中,不可能是快速排序第2趟排序结果的是 ()
正确答案: C 你的答案: A (错误)
4 14 10 12 8 6 18
4 6 10 8 12 14 18
6 4 10 8 14 12 18
8 4 6 10 12 14 18
快排的思想是首先安置分界点到正确的位置,所以排序后,分界点前的数都小于这个数,分界点后的数都大于这个数
每趟排序就有一个元素排在了最终的位置上。那么就是说,第n趟结束,至少有n个元素已经排在了最终的位置上。
红黑树
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
下图中这棵树,就是一颗典型的红黑树:
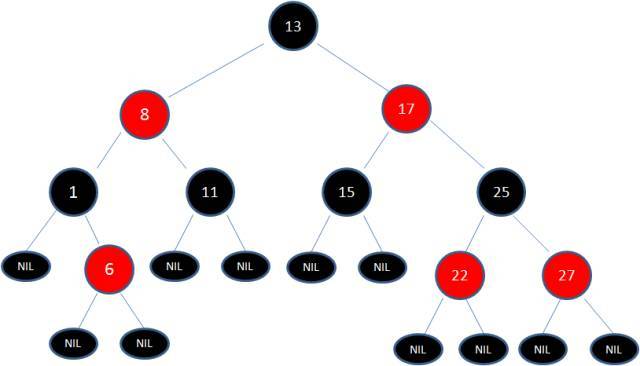
漫画算法:什么是红黑树?
面试旧敌之红黑树(直白介绍深入理解)
插入后调整红黑树结构
红黑树的第 5 条特征规定,任一节点到它子树的每个叶子节点的路径中都包含同样数量的黑节点。也就是说当我们往红黑树中插入一个黑色节点时,会违背这条特征。
同时第 4 条特征规定红色节点的左右孩子一定都是黑色节点,当我们给一个红色节点下插入一个红色节点时,会违背这条特征。
因此我们需要在插入黑色节点后进行结构调整,保证红黑树始终满足这 5 条特征。
调整思想
前面说了,插入一个节点后要担心违反特征 4 和 5,数学里最常用的一个解题技巧就是把多个未知数化解成一个未知数。我们这里采用同样的技巧,把插入的节点直接染成红色,这样就不会影响特征 5,只要专心调整满足特征 4 就好了。这样比同时满足 4、5 要简单一些。
染成红色后,我们只要关心父节点是否为红,如果是红的,就要把父节点进行变化,让父节点变成黑色,或者换一个黑色节点当父亲,这些操作的同时不能影响 不同路径上的黑色节点数一致的规则。
注:插入后我们主要关注插入节点的父亲节点的位置,而父亲节点位于左子树或者右子树的操作是相对称的,这里我们只介绍一种,即插入位置的父亲节点为左子树。
【插入、染红后的调整有 2 种情况:】
情况1.父亲节点和叔叔节点都是红色:
假设插入的是节点 N,这时父亲节点 P 和叔叔节点 U 都是红色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,这时不管 N 是 P 的左孩子还是右孩子,只要同时把 P 和 U 染成黑色,G 染成红色即可。这样这个子树左右两边黑色个数一致,也满足特征 4。
但是这样改变后 G 染成红色,G 的父亲如果是红色岂不是又违反特征 4 了?
这个问题和我们插入、染红后一致,因此需要以 爷爷节点 G 为新的调整节点,再次进行调整操作,以此循环,直到父亲节点不是红的,就没有问题了。
情况2.父亲节点为红色,叔叔节点为黑色:
假设插入的是节点 N,这时父亲节点 P 是红色,叔叔节点 U 是黑色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,但是直接把父亲节点 P 涂成黑色也不行,这条路径多了个黑色节点。怎么办呢?
既然改变不了你,那我们就此别过吧,我换一个更适合我的!
我们怎么把 P 弄走呢?看来看去,还是右旋最合适,通过把 爷爷节点 G 右旋,P 变成了这个子树的根节点,G 变成了 P 的右子树。
右旋后 G 跑到了右子树上,这时把 P 变成黑的,多了一个黑节点,再把 G 变成红的,就平衡了!
上面讲的是插入节点 N 在父亲节点 P 的左孩子位置,如果 N 是 P 的右孩子,就需要多进行一次左旋,把情况化解成上述情况。
N 位于 P 的右孩子位置,将 P 左旋,就化解成上述情况了。
教你如何迅速秒杀掉:99%的海量数据处理面试题
处理海量数据问题,无非就是:
1.分而治之/hash映射 + hash统计 + 堆/快速/归并排序;
2.双层桶划分
3.Bloom filter/Bitmap;
4.Trie树/数据库/倒排索引;
5.外排序;
6.分布式处理之Hadoop/Mapreduce。
第一部分、从set/map谈到hashtable/hash_map/hash_set
一般来说,STL容器分两种,
1.序列式容器(vector/list/deque/stack/queue/heap),
2.关联式容器。
关联式容器又分为set(集合)和map(映射表)两大类,以及这两大类的衍生体multiset(多键集合)和multimap(多键映射表),这些容器均以RB-tree完成。
此外,还有第3类关联式容器,如hashtable(散列表),以及以hashtable为底层机制完成的hash_set(散列集合)/hash_map(散列映射表)/hash_multiset(散列多键集合)/hash_multimap(散列多键映射表)。
也就是说,set/map/multiset/multimap都内含一个RB-tree,而hash_set/hash_map/hash_multiset/hash_multimap都内含一个hashtable。
所谓关联式容器,类似关联式数据库,每笔数据或每个元素都有一个键值(key)和一个实值(value),即所谓的Key-Value(键-值对)。当元素被插入到关联式容器中时,容器内部结构(RB-tree/hashtable)便依照其键值大小,以某种特定规则将这个元素放置于适当位置。
包括在非关联式数据库中,比如,在MongoDB内,文档(document)是最基本的数据组织形式,每个文档也是以Key-Value(键-值对)的方式组织起来。一个文档可以有多个Key-Value组合,每个Value可以是不同的类型,比如String、Integer、List等等。
因为set/map/multiset/multimap都是基于RB-tree之上,所以有自动排序功能,而hash_set/hash_map/hash_multiset/hash_multimap都是基于hashtable之上,所以不含有自动排序功能,至于加个前缀multi_无非就是允许键值重复而已。
字典树(Trie树)实现与应用
查找——图文翔解HashTree(哈希树)
17.位操作符作用:
判断奇偶:因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。
交换两数:a ^= b;b ^= a;a ^= b;。位运算符满足交换律,任何数与0异或不变。
变换符号以及取绝对值:1111 0101(二进制) –取反-> 0000 1010(二进制) –加1-> 0000 1011(二进制)
位运算试题:
1:
有一个数只出现一次而且其它数字都出现了偶数次。用搜索来做就没必要了,利用异或运算的两个特性——1.自己与自己异或结果为0,2.异或满足交换律。因此我们将这些数字全异或一遍,结果就一定是那个仅出现一个的那个数。
2:
在一个数组中除两个数字只出现1次外,其它数字都出现了2次, 要求尽快找出这两个数字。
由于A,B肯定是不相等的,因此在二进制上必定有一位是不同的。根据这一位是0还是1可以将A,B分开到A组和B组。将所有数字异或得到这A,B异或结果,结果中位为1的位就是二者不相同的位。设该位为第j位,则遍历所有的数字,并且左移j位与1相与可以将数字分为两组,然后组内依次异或可以得到A,B.
3.
除了某一个数字x之外,其他数字都出现了三次,而x出现了一次.
遍历所有数字,统计各个位上1的个数,不是三的倍数的位j就表示多了一个X。
for (j = 0; j < 32; j++)
if (bits[j] % 3 != 0)
result += (1 << j);


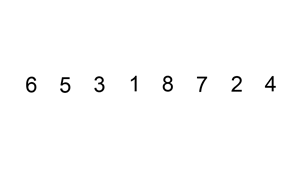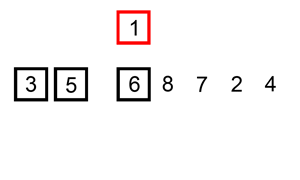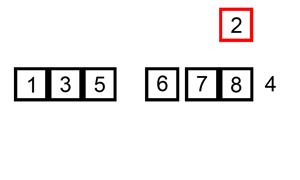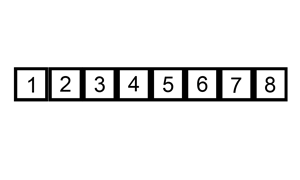

 浙公网安备 33010602011771号
浙公网安备 33010602011771号