机器学习模型评价（未完）

机器学习模型评价(Evaluating Machine Learning Models)-主要概念与陷阱

总结：

离线评估：经常使用的有准确率（accuracy）、精确率－召回率（precision－recall）

在线评估：一般使用一些商业评价指标，如用户生命周期值（customer lifetime value）、广告点击率（click through rate）、用户流失率（customer churn rate）等，这些指标才是模型使用者最终关心的一些指标。

分布漂移（Distribution Drift）：

在机器学习中，很多模型都是假设数据的分布是一定的，不变的，即历史数据与将来的数据都服从相同的分布。但是，在现实生活中，这种假设往往是不成立的，即数据的分布会随着时间的移动而改变，有时甚至变化得很急剧

例如，在文章推荐系统中，文章的主题集数目和主题的发生频率可能是每天改变的，甚至每个小时都在改变，昨天流行的主题在今天可能就不再流行了。如在新闻推荐中，新闻主题就变更得非常快。

解决方法：

使用一些验证指标对模型在不断新生的数据集上进行性能跟踪。如果指标值能够达到模型构建时的指标值，那么表示模型能够继续对当前数据进行拟合。当性能开始下降时，说明该模型已经无法拟合当前的数据了，因此需要对模型进行重新训练了。

性能评价指标:

在垃圾邮件检测系统中，它本身是一个二分类问题（垃圾邮件vs正常邮件），可以使用准确率（Accuracy）、对数损失函数（log-loss）、AUC等评价方法。

在股票预测中，它本身是一个实数序列数据预测问题，可以使用平方根误差（root mean square error， RMSE）等指标

在搜索引擎中进行与查询相关的项目排序中，可以使用精确率－召回率（precision-recall）、NDCG（normalized discounted cumulative gain）。

 

分类评价指标：

分类包括二分类与多分类

准确率(Accuracy)

  准确率是指在分类中，使用测试集对模型进行分类，分类正确的记录个数占总记录个数的比例： 

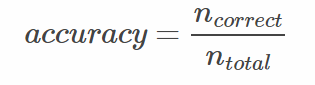
缺点：

准确率评价指标没有对不同类别进行区分，即其平等对待每个类别。

因为不同类别下分类错误的代价不同，即对不同类别的偏向不同，比如有句话为“宁可错杀一万，不可放过一千“就是这个道理，例如在病患诊断中，诊断患有癌症实际上却未患癌症（False Positive）与诊断未患有癌症的实际上却患有癌症（False Negative）的这两种情况的重要性不一样。

另一个原因是，可能数据分布不平衡，即有的类别下的样本过多，有的类别下的样本个数过少，两类个数相差较大。这样，样本占大部分的类别主导了准确率的计算，为了解决这个问题，对准确率进行改进，得到平均准确率。

 

平均准确率(Average Per-class Accuracy)

为了应对每个类别下样本的个数不一样的情况，对准确率进行变种，计算每个类别下的准确率，然后再计算它们的平均值。

举例，类别0的准确率为80%，类别1下的准确率为97.5%，那么平均准确率为(80%+97.5%)/2=88.75%。

如果每个类别下类别的样本个数不一样，即计算每个类别的准确率时，分母不一样，则平均准确率不等于准确率

如果每个类别下的样本个数一样，则平均准确率与准确率相等。 

缺点：

比如，如果存在某个类别，类别的样本个数很少，那么使用测试集进行测试时（如k-fold cross validation），可能造成该类别准确率的方差过大（？？？），意味着该类别的准确率可靠性不强。

对数损失函数(Log-loss)

  在分类输出中，若输出不再是0-1，而是实数值，即属于每个类别的概率，那么可以使用Log-loss对分类结果进行评价。

　　这个输出概率表示该记录所属的其对应的类别的置信度。

　　公式：

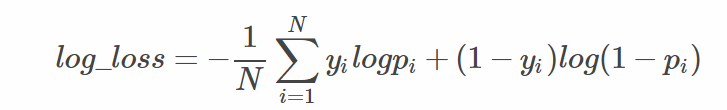（1）

　　上式是交叉熵损失函数，下面是交叉熵定义，交叉熵用于度量两个概率分布间的差异性信息，

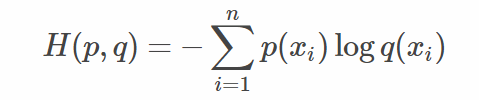（2）

　（1）式yi为0即分类为0， 0*logp_i+1*log(1-p_i) =log(1-p_i) 

　也就是（1）式中的两个部分对于每个样本只会选择其一，因为有一个一定为0

　　信息熵是对事情的不确定性进行度量，不确定越大，熵越大。交叉熵包含了真实分布的熵加上假设与真实分布不同的分布的不确定性。因此，log-loss是对额外噪声(extra noise)的度量，这个噪声是由于预测值域实际值不同而产生的。因此最小化交叉熵，便是最大化分类器的准确率。

　　交叉熵表示2个概率分布的差异性：差异越大则交叉熵越大，差异越小则交叉熵越小，特别地，若2者相同则熵为0。

 

　　交叉熵可在神经网络(机器学习)中作为损失函数，p表示真实标记的分布，q则为训练后的模型的预测标记分布，交叉熵损失函数可以衡量p与q的相似性。交叉熵作为损失函数还有一个好处是使用sigmoid函数在梯度下降时能避免均方误差损失函数学习速率降低的问题，因为学习速率可以被输出的误差所控制。

如何通俗的解释交叉熵与相对熵?

 

验证集获取：

当模型已经对训练集进行了很好的拟合，但是它在新的数据集上的效果则有待验证，因此需要使用与训练集独立的新的数据集对模型进行训练，确保该模型在新的数据集上也能够满足要求。

一般的解决方法是将已有的数据集随机划分成两个个部分，一个用来训练模型，另一个用来验证与评估模型。

另一种方法是重采样，即对已有的数据集进行有放回的采样，然后将数据集随机划分成两个部分，一个用来训练，一个用来验证。

至于具体的做法有hold-out validation、k-fold cross-validation、bootstrapping与jackknife resampling

超参数的调优：

模型参数使指通过模型训练中的学习算法而进行调整的，而模型超参数不是通过学习算法而来的，但是同样也需要进行调优。

举例，我们在对垃圾邮件检测进行建模时，假设使用logistic回归。那么该任务就是在特征空间中寻找能够将垃圾邮件与正常邮件分开的logistic函数位置，于是模型训练的学习算法便是得到各个特征的权值，从而决定函数的位置。但是该学习算法不会告诉我们对于该任务需要使用多少个特征来对一封邮件进行表征，特征的数目这个参数便是该模型的超参数。 

常见方法：

格搜索（grid search）、随机搜索（random search）以及启发式搜索（smart search）等