AUC ROC PR曲线
ROC曲线:
横轴:假阳性率 代表将负例错分为正例的概率
纵轴:真阳性率 代表能将正例分对的概率
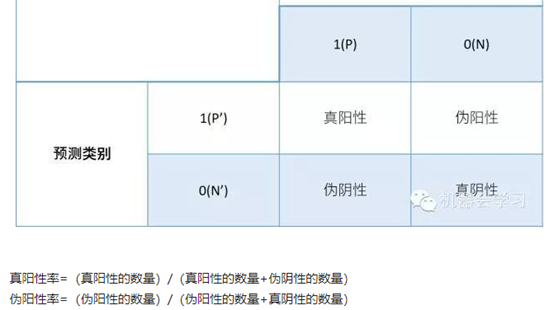
AUC是ROC曲线下面区域得面积。
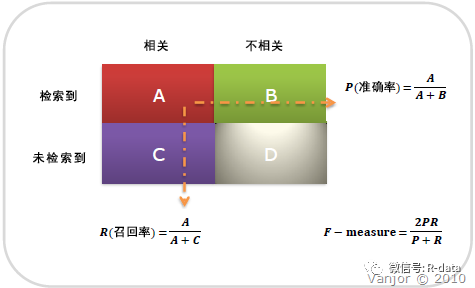
与召回率对比:
AUC意义:
任取一对(正、负)样本,把正样本预测为1的概率大于把负样本预测为1的概率的概率。基于上述,AUC反映的是分类器对样本的排序能力,如果进行随机预测,那么AUC的值应该为0.5.另外AUC对样本类别是否均衡并不敏感,所以不均衡样本通常使用AUC作为评价分类器的标准。
首先AUC值是一个概率值,当你随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然,AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
AUC面积的数值不会大于1。ROC曲线一般都处于y=x这条直线的上方-->AUC的取值范围在0.5和1之间
使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好,而作为一个数值,对应AUC更大的分类器效果更好。
0,1 都靠中心斜线,主要看中间段,中间段正样本排前面的越多,属于正样本的概率值大且这个大概率符合实际情况(真阳性),序列前面大部分都是正样本而模型预测的偏向将它们预测为正样本,负样本排后面,这样曲线就会往左上靠拢,模型的效果就越好
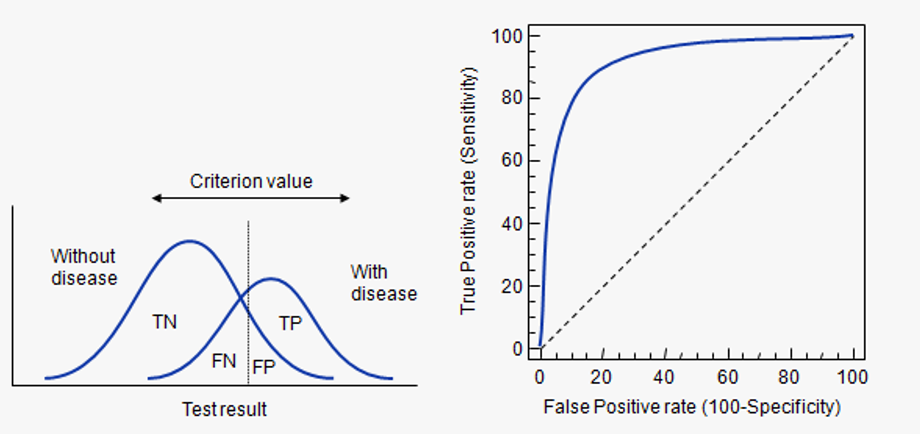
AUC画图例子
假如我们已经得到了所有样本的概率输出(属于正样本的概率),现在的问题是如何改变“discrimination threashold”?我们根据每个测试样本属于正样本的概率值从大到小排序。下图是一个示例,图中共有20个测试样本,“Class”一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属于正样本的概率。

接下来,我们从高到低,依次将“Score”值作为阈值threshold,当测试样本属于正样本的概率大于或等于这个threshold时,我们认为它为正样本,否则为负样本。举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。每次选取一个不同的threshold,我们就可以得到一组FPR和TPR,即ROC曲线上的一点。这样一来,我们一共得到了20组FPR和TPR的值,将它们画在ROC曲线的结果如下图:
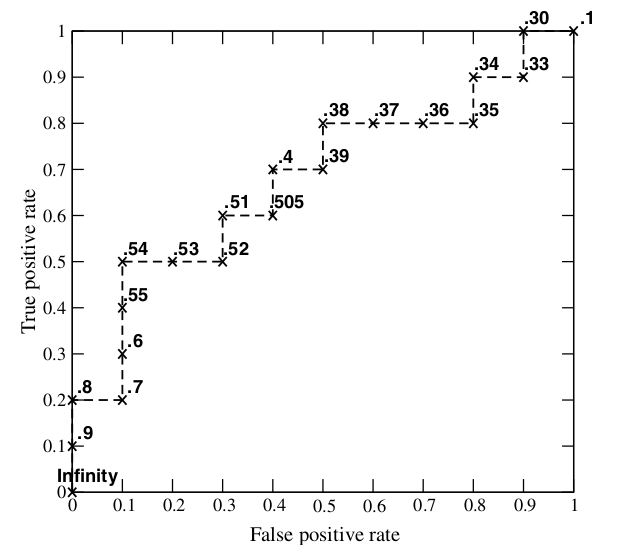
当我们将threshold设置为1和0时,分别可以得到ROC曲线上的(0,0)和(1,1)两个点。将这些(FPR,TPR)对连接起来,就得到了ROC曲线。当threshold取值越多,ROC曲线越平滑。
为什么要使用ROC和AUC呢?
ROC曲线有个很好的特性:当测试集中的正负样本的分布变化的时候,ROC曲线能够保持不变。
AUC对样本类别是否均衡并不敏感,所以不均衡样本通常使用AUC作为评价分类器的标准。
http://alexkong.net/2013/06/introduction-to-auc-and-roc/
PR曲线
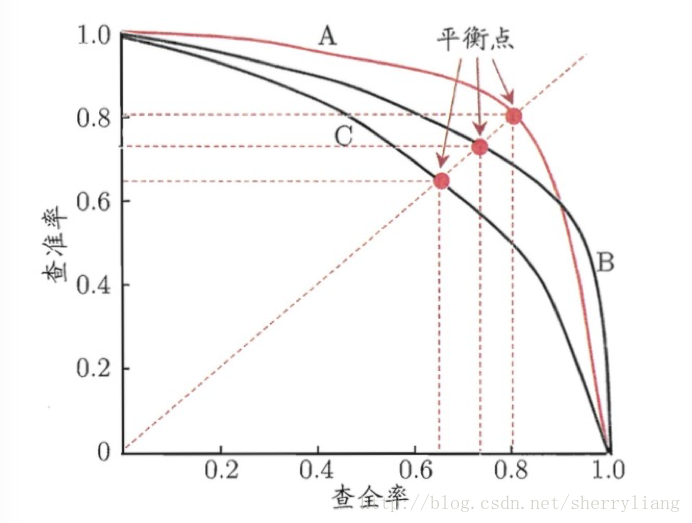
P-R图直观地显示出学习器在样本总体上的查全率和查准率。在进行比较时,若一个学习器的P-R曲线完全被另一个学习器的曲线完全“包住”,则我们就可以断言后者的性能优于前者。
准确率(accuracy),其定义是: 对于给定的测试数据集,分类器正确分类的样本数与总样本数之比。不适合不平衡数据
Precision 和Recall
在linear model中,我们对各个特征线性组合,得到linear score,然后确定一个threshold,linear score < threshold 判为负类,linear score > threshold 判为正类。画PR曲线时, 我们可以想象threshold 是不断变化的。首先,threshold 特别大,这样木有一个是正类,我们计算出查全率与查准率; 然后 threshold 减小, 只有一个正类,我们计算出查全率与查准率;然后 threshold再减小,有2个正类,我们计算出查全率与查准率;threshold减小一次,多出一个正类,直到所有的类别都被判为正类。 然后以查全率为横坐标,差准率为纵坐标,画出图形即可。
例如,有
| 实际类别 | linear score | threshold 为6 | threshold 为5 | threshold 为4 | threshold 为3 | threshold 为2 | threshold 为1 | |
| + | 5.2 | - | + | + | + | + | + | |
| + | 4.45 | - | - | + | + | + | + | |
| - | 3.5 | - | - | - | + | + | + | |
| - | 2.45 | - | - | - | - | + | + | |
| - | 1.65 | - | - | - | - | - | + | |
| 0/0 | 1 / 1 | 2 / 2 | 2 / 3 | 2 / 4 | 2 / 5 | 查准率 | ||
| 0/2 | 1 / 2 | 2 / 2 | 2/ 2 | 2 / 2 | 2/ 2 | 差全率 | ||
| 0/2 | 1/2 | 2/2 | 2/2 | 2/2 | 2/2 | TPR | ||
| 0/3 | 0/3 | 1/3 | 2/3 | 3/3 | FPR |
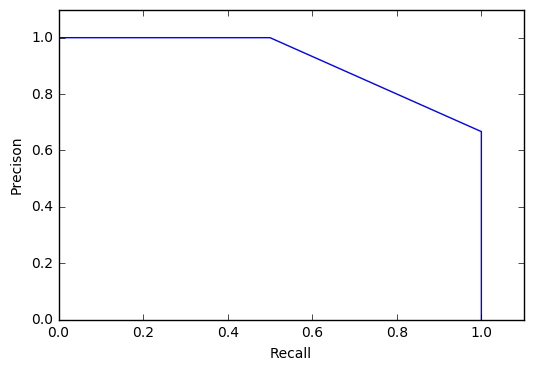
绘制pr曲线代码
import matplotlib import numpy as np import matplotlib.pyplot as plt Recall = np.array([0,1/2,2/2,2/2,2/2,2/2]) Precison = np.array([1/1,2/2,2/3,2/4,2/5,0]) plt.figure() plt.ylim(0,1.1) plt.xlabel("Recall") plt.xlim(0,1.1) plt.ylabel("Precison") plt.plot(Recall,Precison) plt.show()
ROC和PR曲线的选择
如果负样本对于问题没有多大价值,或者负样本比例很大。 那么,PR曲线通常更合适。
比如样本正负比例非常不平衡,且正样本非常少,那我们使用PR曲线。 举个例子:欺诈检测,其中非欺诈样本可能为10000,而欺诈样本可能低于100。
否则ROC会更有用




 浙公网安备 33010602011771号
浙公网安备 33010602011771号