LGV引理学习笔记
Reference
介绍
LGV引理(Lindström–Gessel–Viennot lemma)用来解决有向无环图上不相交路径计数,注意仅适用于有向无环图。
给定 \(n\) 个起点构成的集合 \(S\) 和 \(n\) 个终点构成的集合 \(T\),定义 \(\omega(P)\) 表示路径 \(P\) 上所有边权的乘积(计数时设边权为 \(1\) 即可),\(e(u,v)\) 表示 \(u\) 到 \(v\) 的每一条路径的 \(\omega(P)\) 之和,即 \(e(u,v)=\sum\limits_{P:u \to v}\omega(P)\)。
一组 \(S \to T\) 的不相交路径 \(S\):\(S_i\) 是一条从 \(A_i\) 到 \(B_{\sigma(S)_i}\) 的路径,其中 \(\sigma(S)\) 是 \(S\) 的一个排列,满足对于任意 \(i \ne j\),\(S_i\) 和 \(S_j\) 没有公共顶点。
设 \((-1)^\sigma\) 表示 \((-1)^c\),其中 \(c\) 是排列 \(\sigma\) 的逆序对个数,那么有如下LGV引理:
记 \(n\) 阶方阵
那么
其中 \(\sum\limits_{P:S \to T}\) 中的 \(P\) 表示一个上文中所说的两两无交点的路径组,\(P_i\) 表示这个路径组中以 \(S_i\) 为起点的那条路径。
证明: 由行列式定义,
将 \(\prod_{i=1}^{n}\sum_{P:S_i \to T_{\sigma(i)}} \omega(P)\) 的 \(\sum\) 打开(即 \((a+b)(c+d)\) 打开成 \(ac+ad+bc+bd\) 的形式)可以发现上式就等于所有从 \(S\) 到 \(T\),排列为 \(\sigma\) 的路径组 \(P\) 的 \(\omega(P)\) 之和,于是
此处的 \(P\) 为任意路径组,将它拆成不相交路径组 \(U\) 和相交路径组 \(V\),于是上式等于
若有一个路径组中的某两条路径相交,那么交换两个终点可以得到另外一个相交的方案,并且它们的逆序数不同,不难发现到这是个双射,因此有 \(\sum_{V: S \to T} (-1)^V \prod_{i=1}^{n}\omega(V_i)=0\),于是得到
证毕!
例题
CF348D. Turtles
简要题意
一个 \(n \times m\) 网格图,从一个点 \((x,y)\) 可以走到 \((x+1,y)\) 或者 \((x,y+1)\),某些点被钦定不能走,求无序路径对 \((P_1,P_2)\) 的数量,满足 \(P_1,P_2\) 都以 \((1,1)\) 为起点,\((n,m)\) 为终点,并且两条路径只在起点和终点处有交点。
对于 \(100\%\) 的数据,\(2 \le n,m \le 3000\),答案对 \(10^9+7\) 取模。
题解
注意到两条路径的第一步必然是分别走到 \((1,2)\) 和 \((2,1)\),最后一步必然是分别从 \((n-1,m)\) 和 \((n,m-1)\) 走到 \((n,m)\),直接套用LGV引理,设 \(f(u,v)\) 表示从 \(u\) 到 \(v\) 的路径数量,那么答案就是
依据是:不相交的路径组必然是从 \((1,2)\) 到 \((n-1,m)\),从 \((2,1)\) 到 \((n,m-1)\),符号是正的。
这也是大部分LGV引理题的通用性质:符合条件的排列本质上只有一种。
\(f\) 可以网格图上dp算,时间复杂度 \(\mathcal{O}(nm)\)。
code for CF348D
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3010, MOD = 1e9 + 7;
int n, m; char G[maxn][maxn];
int f[maxn][maxn];
int F(int x, int y) {
if(x <= 0 || y <= 0) return 0;
if(f[x][y] != -1) return f[x][y];
if(G[x][y] == '#') return (f[x][y] = 0);
return (f[x][y] = (F(x - 1, y) + F(x, y - 1)) % MOD);
}
inline int F(int a, int b, int x, int y) {
memset(f, -1, sizeof f); f[a][b] = 1;
if(G[a][b] == '#') return 0;
return F(x, y);
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i ++)
cin >> (G[i] + 1);
long long res = 1ll * F(1, 2, n - 1, m) * F(2, 1, n, m - 1) % MOD - 1ll * F(1, 2, n, m - 1) * F(2, 1, n - 1, m) % MOD;
cout << (res % MOD + MOD) % MOD << '\n';
return 0;
}
HDU5852. Intersection is not allowed!
简要题意
有一个 \(n\times n\) 的棋盘,一个棋子从 \((x, y)\) 只能走到 \((x, y+1)\) 或 \((x + 1, y)\) ,有 \(k\) 个棋子,一开始第 \(i\) 个棋子放在 \((1, a_i)\) ,最终要到 \((n, b_i)\) ,路径要两两不相交,求方案数对 \(10^9+7\) 取模。
对于 \(100\%\) 的数据,保证 \(1\le n\le 10^5\) , \(1\le k\le 100\) ,保证 \(1\le a_1<a_2<\dots<a_n\le n\) , \(1\le b_1<b_2<\dots<b_n\le n\) 。
题解
因为 \(a,b\) 都是递增的,所以不相交的路径组的匹配方案是固定的,两点之间的路径数量就是个组合数,直接套LGV引理就行。
时间复杂度 \(\mathcal{O}(n + k^3+ k^2\log P)\)。
code for HDU5852
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, K = 110, MOD = 1e9 + 7;
inline int Plus(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b; }
inline int Minus(int a, int b) {return a - b < 0 ? a - b + MOD : a - b; }
inline int ksm(long long a, int b) {
long long r = 1;
for(; b; b >>= 1, a = a * a % MOD)
if(b & 1) r = r * a % MOD;
return r;
}
int n, k, A[K], B[K];
int fac[N], ifac[N];
inline int C(int a, int b) {return a >= b && b >= 0 ? 1ll * fac[a] * ifac[b] % MOD * ifac[a - b] % MOD : 0; }
int Mat[K][K];
inline int det() {
int flag = 1, ans = 1;
for(int i = 1; i <= k; i ++) {
if(!Mat[i][i]) {
for(int j = i + 1; j <= k; j ++)
if(Mat[j][i]) {
swap(Mat[i], Mat[j]), flag = -flag;
break;
}
}
if(!Mat[i][i]) return 0;
ans = 1ll * ans * Mat[i][i] % MOD;
long long mul = ksm(Mat[i][i], MOD - 2);
for(int j = i; j <= k; j ++)
Mat[i][j] = Mat[i][j] * mul % MOD;
for(int j = i + 1; j <= k; j ++) {
mul = Mat[j][i];
for(int p = i; p <= k; p ++)
Mat[j][p] = Minus(Mat[j][p], mul * Mat[i][p] % MOD);
}
}
if(flag == -1) ans = Minus(0, ans);
return ans;
}
inline void solve() {
cin >> n >> k;
for(int i = 1; i <= k; i ++)
cin >> A[i];
for(int i = 1; i <= k; i ++)
cin >> B[i];
for(int i = 1; i <= k; i ++)
for(int j = 1; j <= k; j ++) {
if(A[i] <= B[j]) Mat[i][j] = C((n - 1) + (B[j] - A[i]), n - 1);
else Mat[i][j] = 0;
}
cout << det() << '\n';
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
fac[0] = 1;
for(int i = 1; i < N; i ++) fac[i] = 1ll * fac[i - 1] * i % MOD;
ifac[N - 1] = ksm(fac[N - 1], MOD - 2);
for(int i = N - 1; i >= 1; i --) ifac[i - 1] = 1ll * ifac[i] * i % MOD;
int T; cin >> T;
while(T --) solve();
return 0;
}
[NOI2021] 路径交点
题目描述
小 L 有一个有向图,图中的顶点可以分为 \(k\) 层,第 \(i\) 层有 \(n_i\) 个顶点,第 \(1\) 层与第 \(k\) 层顶点数相同,即 \(n_1 = n_k\),且对于第 \(j\)(\(2 \leq j \leq k-1\))层,\(n_1 \leq n_j \leq 2n_1\)。对于第 \(j\)(\(1 \leq j < k\))层的顶点,以它们为起点的边只会连向第 \(j + 1\) 层的顶点。没有边连向第 \(1\) 层的顶点,第 \(k\) 层的顶点不会向其他顶点连边。
现在小 L 要从这个图中选出 \(n_1\) 条路径,每条路径以第 \(1\) 层顶点为起点,第 \(k\) 层顶点为终点,并要求图中的每个顶点至多出现在一条路径中。更具体地,把每一层顶点按照 \(1,2,\ldots,n_1\) 进行编号,则每条路径可以写为一个 \(k\) 元组 \((p_1,p_2,\ldots,p_k)\),表示这条路径依次经过第 \(j\) 层的 \(p_j\)(\(1 \leq p_j \leq n_j\))号顶点,并且第 \(j\)(\(1 \leq j < k\))层的 \(p_j\) 号顶点有一条边连向第 \(j+1\) 层的第 \(p_{j+1}\) 号顶点。
小 L 把这些路径画在了纸上,发现它们会产生若干个交点。对于两条路径 \(P,Q\),分别设它们在第 \(j\) 层与第 \(j+1\) 层之间的连边为 \((P_j,P_{j+1})\) 与 \((Q_j,Q_{j+1})\),若,
则称它们在第 \(j\) 层后产生了一个交点。两条路径的交点数为它们在第 \(1, 2,\ldots,k - 1\) 层后产生的交点总数。对于整个路径方案,它的交点数为两两不同路径间交点数之和。例如下图是一个 \(3\) 条路径,共 \(3\) 个交点的例子,其中红色点是交点。
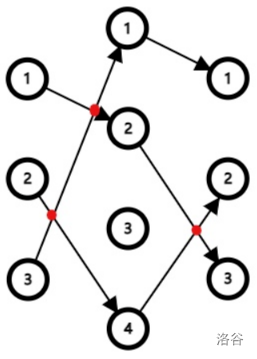
小 L 现在想知道有偶数个交点的路径方案数比有奇数个交点的路径方案数多多少个。两个路径方案被视为相同的,当且仅当它们的 \(n_1\) 条路径按第一层起点编号顺序写下的 \(k\) 元组能对应相同。由于最后的结果可能很大,请你输出它对 \(998244353\)(一个大质数)取模后的值。
输入格式
本题有多组数据,输入数据第一行一个正整数 \(T\) ,表示数据组数。对于每组数据:
第一行一个正整数 \(k\),表示一共有 \(k\) 层顶点。
第二行包含 \(k\) 个整数 \(n_1,n_2,\ldots,n_k\),依次表示每一层的顶点数量。保证 \(n_1=n_k\),且 \(n_1 \leq n_i \leq 2n_1\)(\(2 \leq i \leq k-1\))。
第三行包含 \(k-1\) 个整数 \(m_1,m_2,\ldots,m_{k-1}\),依次表示第 \(j\) 层顶点到第 \(j+1\) 层顶点的边数。保证 \(m_j \leq n_j \times n_{j+1}\)。
接下来有 \(k-1\) 段输入。第 \(j\)(\(1 \leq j < k\))段输入包含 \(m_j\) 行,每一行两个整数 \(u,v\),表示第 \(j\) 层的 \(u\) 号顶点有一条边连向第 \(j+1\) 层的 \(v\) 号顶点。
数据保证图中不会出现重边。
输出格式
输出共 \(T\) 行,每行一个整数,表示该组数据的答案对 \(998244353\) 取模后的值。
样例
样例输入 #1
1
3
2 3 2
4 4
1 1
1 2
2 1
2 3
1 2
2 1
3 1
3 2
样例输出 #1
1
偶数个交点的方案有 \(2\) 个,奇数个交点的方案有 \(1\) 个,所以答案为 \(1\)。
将下表中路径 \(1\) 和路径 \(2\) 的方案交换,将会得到相同的方案,例如路径 \(1\) 为 \((2, 3, 1)\) 且路径 \(2\) 为 \((1, 1, 2)\) 的方案与方案 \(1\) 是相同的方案,所以不会被计入答案。
| 路径方案 | 路径 \(1\) | 路径 \(2\) | 交点总数 |
|---|---|---|---|
| \(1\) | \((1,1,2)\) | \((2,3,1)\) | \(1\) |
| \(2\) | \((1,2,1)\) | \((2,1,2)\) | \(2\) |
| \(3\) | \((1,2,1)\) | \((2,3,2)\) | \(0\) |
数据范围
对于所有测试数据:\(2 \leq k \leq 100\),\(2 \leq n_1 \leq 100\),\(1 \leq T \leq 5\)。
每个测试点中,保证 \(n_1 > 10\) 的数据只有 \(1\) 组。
| 测试点编号 | \(k=\) | \(n_1 \leq\) | 特殊性质 |
|---|---|---|---|
| \(1 \sim 4\) | \(2\) | \(10\) | 无 |
| \(5 \sim 6\) | \(10\) | \(10\) | A,B |
| \(7 \sim 8\) | \(10\) | \(10\) | A |
| \(9 \sim 10\) | \(10\) | \(10\) | 无 |
| \(11 \sim 13\) | \(2\) | \(100\) | 无 |
| \(14 \sim 15\) | \(100\) | \(100\) | A,B |
| \(16 \sim 17\) | \(100\) | \(100\) | A |
| \(18 \sim 20\) | \(100\) | \(100\) | 无 |
特殊性质 A:对于所有 \(i\)(\(2 \leq i \leq k-1\))满足 \(n_i = n_1\)。
特殊性质 B:保证路径方案总数至多为 \(1\)。
题解
设第一层的点构成集合 \(S\),最后一层的点构成集合 \(T\),所有路径不交让我们想到LGV引理,更进一步地观察到性质:\(S \to T\) 的逆序对数量与交点数量的奇偶性质的相同的!
于是 \(n_1\) 次BFS求出 \(S\) 中的每个点到 \(T\) 中每个点的路径数量,套板子即可,时间复杂度 \(\mathcal{O}(n_1^3 + n_1^2 \log P)\)。
code for [NOI2021]路径交点
#include <bits/stdc++.h>
using namespace std;
const int N = 210, K = 210, MOD = 998244353;
inline int Plus(int a, int b) {return a + b >= MOD ? a + b - MOD : a + b; }
inline int Minus(int a, int b) {return a - b < 0 ? a - b + MOD : a - b; }
inline int ksm(long long a, int b) {
long long r = 1;
for(; b; b >>= 1, a = a * a % MOD)
if(b & 1) r = r * a % MOD;
return r;
}
int k, n[K], m[K];
vector<int> G[N][N];
int siz[N][N], ind[N][N];
void BFS(int S) {
static int Ind[N][N];
for(int i = 1; i <= k; i ++)
for(int j = 1; j <= n[i]; j ++)
siz[i][j] = 0, Ind[i][j] = ind[i][j];
siz[1][S] = 1;
queue<pair<int, int>> Q;
for(int i = 1; i <= k; i ++)
for(int j = 1; j <= n[i]; j ++)
if(!Ind[i][j]) Q.push({i, j});
while(!Q.empty()) {
auto u = Q.front(); Q.pop();
for(auto v : G[u.first][u.second]) {
siz[u.first + 1][v] = Plus(siz[u.first + 1][v], siz[u.first][u.second]);
if(!--Ind[u.first + 1][v]) Q.push({u.first + 1, v});
}
}
}
int Mat[N][N];
inline int det() {
int flag = 1, ans = 1;
for(int i = 1; i <= n[1]; i ++) {
if(Mat[i][i] == 0) {
for(int j = i + 1; j <= n[1]; j ++)
if(Mat[j][i] != 0) {
swap(Mat[i], Mat[j]), flag = -flag;
break;
}
}
if(Mat[i][i] == 0) return 0;
long long mul = ksm(Mat[i][i], MOD - 2); ans = 1ll * ans * Mat[i][i] % MOD;
for(int j = i; j <= n[1]; j ++) Mat[i][j] = 1ll * Mat[i][j] * mul % MOD;
for(int j = i + 1; j <= n[1]; j ++) {
mul = Mat[j][i];
for(int p = i; p <= n[1]; p ++)
Mat[j][p] = Minus(Mat[j][p], 1ll * mul * Mat[i][p] % MOD);
}
}
if(flag == -1) ans = Minus(0, ans);
return ans;
}
inline void solve() {
cin >> k;
for(int i = 1; i <= k; i ++)
cin >> n[i];
for(int i = 1; i <= k; i ++)
for(int j = 1; j <= n[i]; j ++)
G[i][j].clear(), ind[i][j] = 0;
for(int i = 1; i < k; i ++)
cin >> m[i];
for(int i = 1; i < k; i ++) {
for(int j = 1; j <= m[i]; j ++) {
int a, b; cin >> a >> b;
G[i][a].emplace_back(b);
ind[i + 1][b] ++;
}
}
for(int i = 1; i <= n[1]; i ++) {
BFS(i);
for(int j = 1; j <= n[k]; j ++)
Mat[i][j] = siz[k][j];
}
cout << det() << '\n';
}
int main() {
ios::sync_with_stdio(false), cin.tie(0);
int T; cin >> T;
while(T --) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号