C语言题目五

题目1
题目：Hermite Polynomials（厄米多项式）是这样定义的：

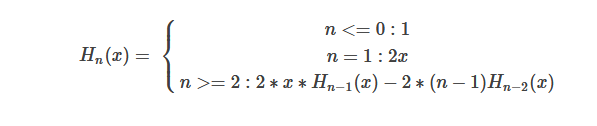例如：当n=3，x=2时，值为40。请编写一个递归函数，计算该函数的值。你的函数应该与下面的原型匹配：
int hermite(int n, int x)
代码如下：

#include<stdio.h>

int hermite(int n, int x)
{
    if (n <= 0)    //特殊条件的处理
    {
        return 1;
    }
    else if (n == 1)  //特殊条件的处理
    {
        return 2 * x;
    }
    else if (n >= 2)  //公式
    {
        return 2 * x* hermite(n - 1, x) - 2 * (n - 1) * hermite(n - 2, x);   //使用递归
    }
}
int main()
{
    printf("%d\n", hermite(3, 2));
    return 0;
}

题目2
题目：两个整数值M和N（M、N均大于0）的最大公约数可以按照下面的方法计算：

gcd(M,N)={M(modN)=0:NM(modN)=R,R>0:gcd(N,R)

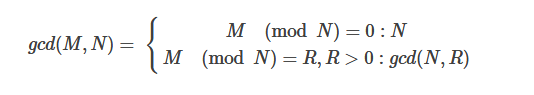请编写一个名叫gcd的函数，它接受两个整形参数，并返回这两个数的最大公约数。如果这两个参数中的任何一个不大于零，函数应该返回零。
代码如下：

#include<stdio.h>
int gcd(int m, int n)
{
    if (m%n == 0)
    {
        return n;
    }
    else if (m % n>0)
    {        
        return gcd(n, m % n);   //函数递归
    }
}
int main()
{
    int value = 0;
    printf("两个数的最大公约数为%d\n", gcd(100,80));
    return 0;
}