P6119 [USACO17FEB]Why Did the Cow Cross the Road II G 题解

我向来是遇到动规就懵逼的那种人......

题目传送门

---

 

大体思路：

拿到一道动态规划题目怎么办？

坦然逝去。

当然是去推状态转移方程啦！

怎么推？

如果你不愿意看，可以直接去看状态转移方程。

一般我会用一个名为 f 的数组去推导（我想这也是大多数人的嗜好）。

我们把 f_i,j 设为取序列 a 的前 i 项，序列 b 的前 j 项的最长公共子序列（ LCS ），那么状态转移方程就是：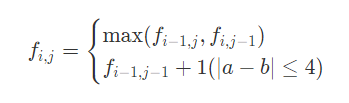

 

 

 

当然，你也可以设为设为取序列 a 的第 i 项，序列 b 的第 j 项的最长公共子序列。但是这样做不但状态转移方程变了，而且似乎还要把 f 数组初始化......

这里提一句，其实推导状态转移方程有技巧的。这里有我总结出来的两种方法：

1. 手打样例，亲手去模拟一下样例，可以发现规律。

2. 根据题目描述。有些题目甚至直接把方程打了出来，就算不是这样我们也可以根据题目给出的蛛丝马迹进行推导。

3. 借鉴题解，参考题解。

---

 

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
#define forr(a,b) for(int i=a;i<=b;i++) //简化一下
#define foor(a,b) for(int j=a;j<=b;j++)
using namespace std;
int a[1001]={0},b[1001]={0};
int f[1001][1001]={0};
int main(){
int n;
cin>>n;
forr(1,n) cin>>a[i];
forr(1,n) cin>>b[i];
forr(1,n){
foor(1,n){
if(abs(a[i]-b[j])<=4){ //abs取绝对值
f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
else{
f[i][j]=max(f[i-1][j],f[i][j-1]);
}
}
}
cout<<f[n][n]<<endl;
return 0;
}

 

---

 

总结：

注意推导状态转移方程的部分。

后记：

大佬们都说这题很简单，不过我觉得对我来说还挺难的。

动态规划我学的一直都不太好，这道题目做的时候我也是参考了题解，希望这篇题解没有错误，但愿能过吧。