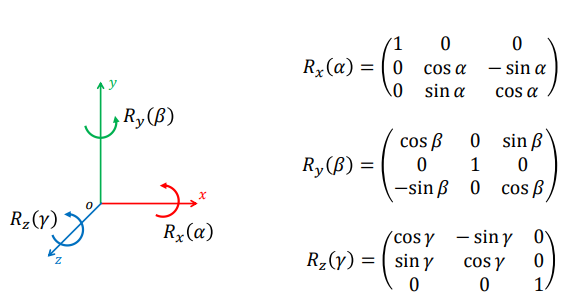GAMES105笔记与理解（二）

线性代数

1. 向量

• 向量是一种同时具有大小和方向的量
  给定一个向量\(\mathbf{a}\)，大小为\(||\mathbf{a}||\)，方向为\(\frac{\mathbf{a}}{||\mathbf{a}||}\)（归一化）
• 可以表示一个位置、特征值....

2. 向量叉乘的两种理解

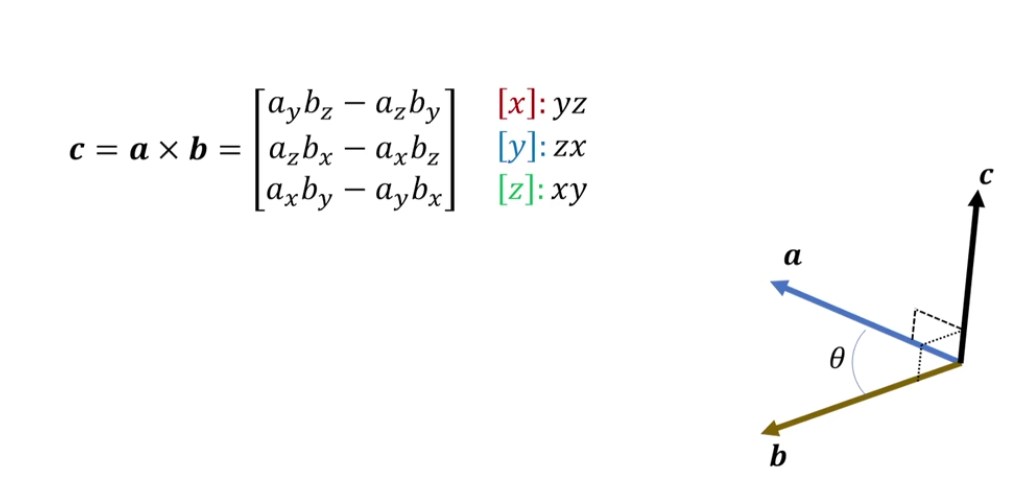
• 叉乘的作用在于寻找一个同时垂直于两个向量的向量，比如法向量

• 给定两个向量，如何求出其中一个向量旋转到另一个向量的最小旋转？利用叉乘得到旋转轴、利用点乘得到最小旋转角

  

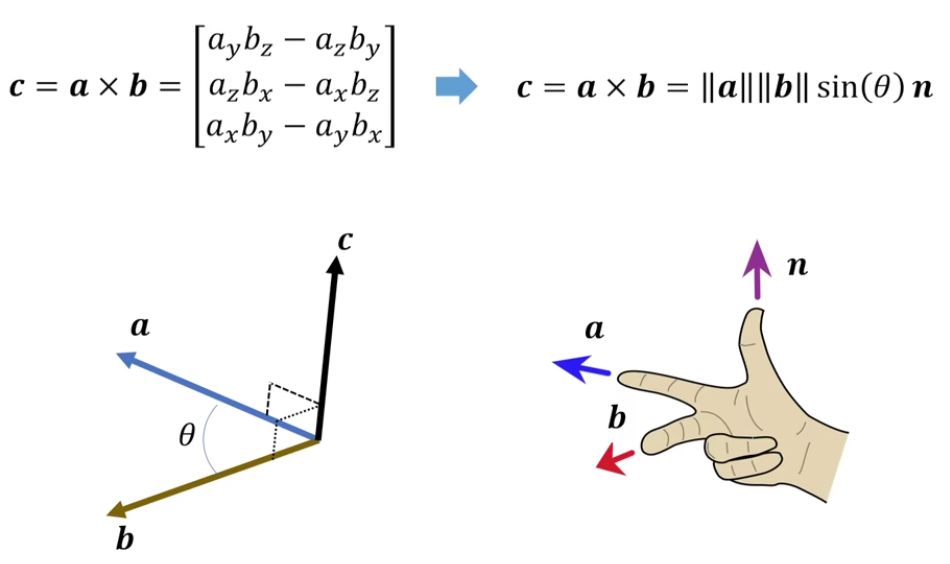
• 如果给定旋转轴u和旋转角\(\theta\)，如何得到旋转后的向量的值？

  • 方向：
    
    这里的v指的是找到一个同时垂直于u和a的方向，t是同时垂直于u和v的方向
  • 大小：在上图的平面上进行推理，如下
    
    这里的\(||\mathbf{u}\times \mathbf{a}||\)是\(\mathbf{a}\)在该平面的投影，是\(\mathbf{a}\)和\(\mathbf{u}\)夹角乘上\(\mathbf{a}\)的值，相当于\(||\mathbf{u}\times \mathbf{a}||\)，即叉乘的长度
    最后得到\(\mathbf{a}\)往\(||\mathbf{v}\)方向移动\(sin\theta\)，往\(||\mathbf{t}\)方向移动\(1-cos\theta\)
  • 总的公式：Robrigues's rotation formula
    \(\mathbf{b}=\mathbf{a}+(sin\theta)\mathbf{u}\times \mathbf{a} +(1-cos\theta)\mathbf{u}\times (\mathbf{u}\times \mathbf{a})\)

3. 矩阵

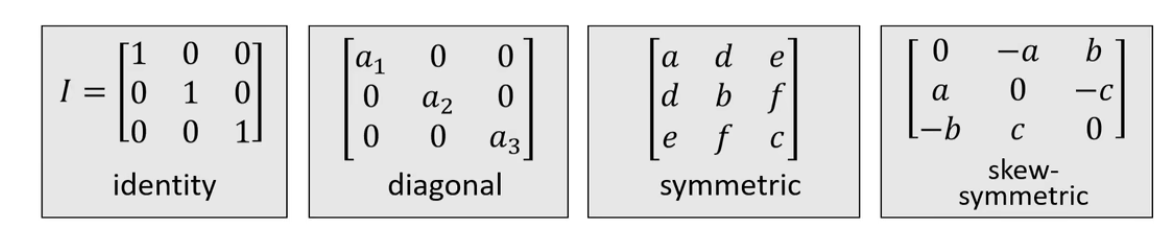
• 特殊矩阵
  

• 矩阵的操作
  

• 叉乘的矩阵形式
  

  叉乘的操作用矩阵形式表示：
  

• 旋转用矩阵表示
  

• 正交阵

  • 定义：所有列（行）是互相构成正交的向量 ———> 产生的性质： \(A^T = A^{-1}\) / \(A^TA=I\)
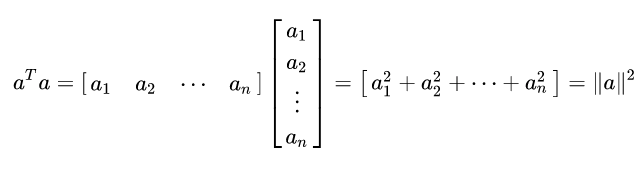
    如图所示，对于矩阵A的的每一列向量来说都是互相正交的，所以其\(\mathbf{a}_i^T\mathbf{a}_j=1\)，对于同一个向量来说，\(\mathbf{a}^T\mathbf{a}\)等于其长度的平方，定义上表示\(\mathbf{a}^T\mathbf{a}=1\)，说明正交矩阵的列向量都是单位向量。
    
    
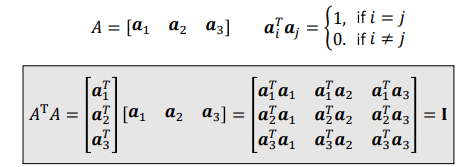
  • 正交阵的行列式是\(\pm 1\)，正负值取决于向量的顺序，如果其向量积满足右手定则，则为+1，否则为-1
  • 对于一个\(3\times 3\)的正交阵\(U\)（奇数阶的正交阵）来说，至少会有一个实的特征值\(\lambda = det U = \pm 1\)

    关于特征值的定义：
    

4. Rigid Transformation

• 旋转矩阵的一些性质
  
• 旋转的组合是从右往左的
  
• 绕着坐标轴旋转的旋转矩阵