《Colorization Using Optimization》论文理解与复现

1. 导读#

本报告的主要内容是阅读《Colorization Using Optimization》论文之后对原理进行理解并利用python复现论文中的照片上色算法。

2. 引言#

在论文发布前现有的技术中，图片上色是一个耗费大量人力、花费较多时间的任务。且“将图像划分为多个区域”常采用自动分割算法，但已存在的自动分割算法无法正确区分模糊或复杂的区域边界，故也导致传统的基于这种自动分割算法的着色是十分不准确的。因此，《Colorization Using Optimization》提出一个简单的Colorization方法，这种方法既不需要精确的图像分割，也不需要精准的图像追踪。这种应方法基于一个统一的框架，却能够同时应用在静态图像和图像序列之上。

3. 技术贡献#

文章的贡献是提出了一种简单但有效的交互式着色算法，并且大大减少了用户所需的输入量。减少了着色工作花费的人力及时间。

4. 方法介绍#

4.1 算法原理#

简单来说，就是对一张灰度图像先人为地进行着色，然后利用优化的方法，对其他的没有颜色的区域进行填充。这些处理都是在 YUV 颜色空间进行的。其中，Y表示的是单色亮度通道，简称为“亮度”；U和V表示色度通道，用来编码颜色。灰度图的Y通道其实就是本身的灰度值。
论文中提到的算法基于一个简单的前提：在时间和空间上具有相似灰度等级的像素也会具有相同的颜色。换句话来说，如果两个像素 $\mathbf r$ 和 $\mathbf s$ 具有相似的亮度，则他们也会有相似的颜色。
这个前提相当于一个约束。因此，该问题被表述为以下优化问题

\begin{matrix} (1) & J (U) = \sum_{r} (U (r) - \sum_{s \in N (r)} w_{r s} U (s))^{2} \end{matrix}

$J(U) = \sum_r (U(r) - \sum_{s \in N(r)}w_{rs}U(s))^2 \tag{1}$

\begin{matrix} (2) & J (V) = \sum_{r} (V (r) - \sum_{s \in N (r)} w_{r s} V (s))^{2} \end{matrix}

$J(V) = \sum_r (V(r) - \sum_{s \in N(r)}w_{rs}V(s))^2 \tag{2}$

这个优化问题表示的是一个约束，即在求解未知U和V的像素时，如果相邻像素具有相似的强度（通道Y），则在求解时它们具有相似的颜色（通道U和V）。否则，它们的颜色应该不太相似。为了表示这个相似性和差异性，我们使用亲和函数。

而其中对于权重的定义，要体现强度的相似性，因此使用了如下的计算公式：

\begin{matrix} (3) & w_{r s} \propto e x p (\frac{- (Y (r) - Y (s))^{2}}{2 σ_{r}^{2}}) \end{matrix}

$w_{rs} \propto exp(\frac{-(Y(r)-Y(s))^2}{2\sigma_r^2}) \tag{3}$

以上就是整个算法地描述，这类算法属于基于距离和色度混合的彩色化算法，其主要思想是：用户设定颜色线条，然后根据某种距离公式计算每一个像素到颜色线条的距离，则距离最近的线条颜色即为该像素的颜色。这种算法最大的优点是速度快，属于快速算法，缺点是单纯考虑了距离的影响，忽略了颜色聚类的影响，也属于半自动算法。

4.2 线性方程组求解#

优化问题最终归结为求解具有闭式最小二乘解形式的线性方程组，对于V通道也要重复相同的操作。上述公式(1)(3)其实等效为求解两个大型线性方程数组，可以写成 $A\mathbf x = b$ 的形式，A是关于W的矩阵，b即是根据U/V通道加权的结果。

为了更好的理解线性方程组求解过程，学习了这个具体例子，有利于代码复现。

给出一个2行3列的图像, 现在灰度图上进行了局部着色，如(2)所示，可以抽出着色部分的U通道，接下来我们的任务是求解其他部分的U值，如(3)所示，剩余的是 $x_2,x_3,x_4,x_6$ 待求解的未知数。V值求解方法一样，灰度图的灰度值本身就是Y，最后我们把YUV合起来就得到了最终的彩色图。

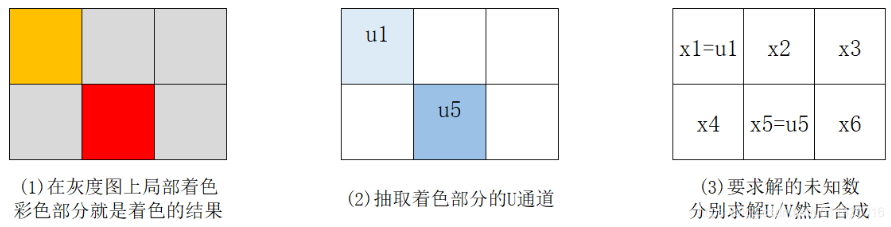
根据图三，可以利用公式(1)来计算，要使得约束问题最小化，则可得需要满足： $U(r) - \sum_{s \in N(r)}w_{rs}U(s)=0$ 。对每个像素进行该约束，可得如下线性方程组：

{\begin{cases} x_{1} = u_{1} \\ x_{2} - w_{21} u_{1} - w_{23} x_{3} - w_{24} x_{4} - w_{25} u_{5} - w_{26} x_{6} = 0 \\ x_{3} - w_{32} x_{2} - w_{35} u_{5} - w_{36} x_{6} = 0 \\ x_{4} - w_{41} u_{1} - w_{42} x_{2} - w_{45} u_{5} = 0 \\ x_{5} = u_{5} \\ x_{6} - w_{62} x_{2} - w_{63} x_{3} - w_{65} u_{5} = 0 \end{cases}

$\begin{cases} x_1 = u_1\\ x_2 - w_{21}u_1 - w_{23}x_3-w_{24}x_4-w_{25}u_5-w_{26}x_6=0 \\ x_3 - w_{32}x_2 - w_{35}u_5-w_{36}x_6=0\\ x_4 - w_{41}u_1 - w_{42}x_2-w_{45}u_5=0\\ x_5 = u_5\\ x_6 - w_{62}x_2 -w_{63}x_3- w_{65}u_5=0 \end{cases}$

该线性方程组可以转换为矩阵相乘形式，如下：

(\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & - w_{23} & - w_{24} & 0 & - w_{26} \\ 0 & - w_{32} & 1 & 0 & 0 & - w_{36} \\ 0 & - w_{42} & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & - w_{62} & - w_{63} & 0 & 0 & 1 \end{matrix}) (\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \\ x_{5} \\ x_{6} \end{matrix}) = (\begin{matrix} u_{1} \\ w_{21} u_{1} + w_{25} u_{5} \\ w_{35} u_{5} \\ w_{41} u_{1} + w_{45} u_{5} \\ u_{5} \\ w_{65} u_{5} \end{matrix})

$\left( \begin{matrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & -w_{23} & -w_{24} & 0 & -w_{26}\\ 0 & -w_{32} & 1 & 0 & 0 & -w_{36}\\ 0 & -w_{42} & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & -w_{62} & -w_{63} & 0 & 0 & 1 \end{matrix} \right) \left( \begin{matrix} x_1\\x_2\\x_3\\x_4\\x_5\\x_6 \end{matrix} \right) = \left( \begin{matrix} u_1\\w_{21}u_1+w_{25}u_5\\w_{35}u_5\\w_{41}u_1+w_{45}u_5\\u_5\\w_{65}u_5 \end{matrix} \right)$

5. 代码复现——基于python的opencv实现#

5.1 数据来源#

论文中的图像都可以通过https://www.cs.huji.ac.il/w~yweiss/Colorization/找到。代码复现时可以将最终的图像转成灰度图，从而作为输入之一。

5.2 算法复现#

厘清整个算法核心思想和思路之后，下面利用python进行复现

具体步骤如下所示：

将原始灰度图像和标记图像转换为从RGB到YUV/YIQ颜色空间。通过查阅资料发现有一个colorsys库可以直接实现转换

Copy
src = cv.imread('hair.bmp') #cv读取的是BGR格式
src = src[..., ::-1] # 第一通道和第三通道互换，实现BGR到RGB转换
_src = src.astype(float) / 255 # 通过上次任务阅读发现很多都是用小数进行运算，这样会更精细一点，不然矩阵运算丢失小数点对结果影响很大

marked = cv.imread('hair_m.bmp')
marked = marked[..., ::-1]
_marked = marked.astype(float) / 255

Y,_,_ = colorsys.rgb_to_yiq(_src[:,:,0],_src[:,:,1],_src[:,:,2]) # Y通道是原灰度图的
_,U,V = colorsys.rgb_to_yiq(_marked[:,:,0],_marked[:,:,1],_marked[:,:,2]) # 待求的U和V是marked图像的

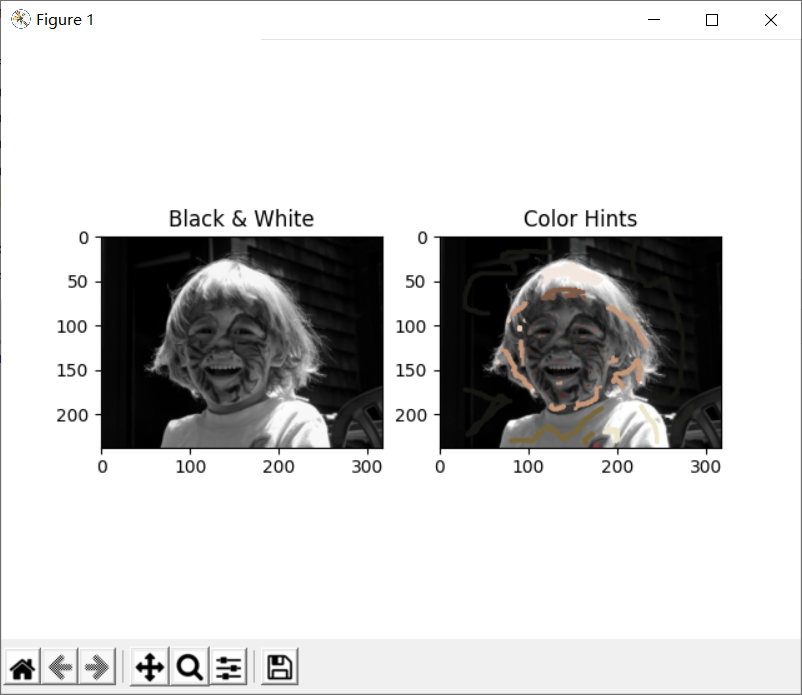
用matplotlib打印出原灰度图像和标记图像，如图所示

计算矩阵 $A$ ，即权重矩阵 $W$ ，该矩阵取决于原始灰度图像中像素的相邻强度的相似性，利用的公式是4.1节的公式(3)

代码实现

主函数

1）统计marked图像中标记过颜色的像素位置，由于没有上色的像素U和V为0，所以可以通过U和V是否为0判断像素是否上过色。需要注意的是UV的取值范围为[-127,128]，所以要加绝对值。

2）假设图像所有像素个数为N，则A矩阵大小为N*N，第i行为第i个像素与其他各像素的权重大小，初始化为0。由于是稀疏矩阵，可以用sparse.lil_matrix来创建

3）遍历每个像素，如果该像素不是已上过色的像素，则找出其相邻像素，计算强度相似性得出结果，将计算结果放入矩阵的对应位置；如果是已标记过颜色的，则跳过计算权重这一步，直接赋值 $A[i,i]=1$

Copy
rows = _src.shape[0]
cols = _src.shape[1]
size = rows * cols 
# 统计marked图像中标记过颜色的像素位置 
hhash = (abs(U) + abs(V)) > 0.0001 # 灰度图的U和V为0，但是有颜色的话就会大于0
W = sparse.lil_matrix((size, size))
# 遍历所有像素
for c in range(cols):
    for r in range(rows):
        # 1. 将该像素的位置和其强度存在center里面，并计算索引
        center = [r, c, yuv[(r, c)][0]]
        c_idx = to_seq(r, c, rows)
        # 2. 如果该像素没有上过色
        if not hhash[r,c]:
            # 2.1 找到该像素的邻居像素
            neighbors = find_neighbors(center, yuv)
            # 2.2 计算权重，weight[0]、weight[1]表示邻居的xy位置，weight[2]表示权重
            weights = affinity_a(neighbors, center)
            # 2.3 放入对应行，因为像素是按顺序遍历的，所以weightData存放的也是按顺序的
            for e in weights:
                # 2.3.1 计算center像素和邻居像素的索引
                n_idx = to_seq(e[0], e[1], rows)
                # 2.3.2 放入矩阵
                W[c_idx, n_idx] = e[2]
        # 3. 如果该像素上过色，则直接放入自己本身的信息，权重为1
        W[c_idx, c_idx] = 1.0
matA = W.tocsr()

find_neighbors函数
1. 求出该像素的邻居遍历范围，同时要考虑像素在边界
2. 在遍历范围中遍历所有的邻居像素，存放邻居像素的xy位置，以及邻居像素的强度，用于后面计算权重

Copy
def find_neighbors(center, pic):
    neighbors = []
    # 1. 求出该像素的邻居遍历范围，同时要考虑像素在边界
    r_min = max(0, center[0] - 1) 
    r_max = min(pic.shape[0], center[0] + 2)
    c_min = max(0, center[1] - 1)
    c_max = min(pic.shape[1], center[1] + 2)
    # 遍历所有的邻居像素
    for r in range(r_min, r_max):
        for c in range(c_min, c_max):
            # 自己本身忽略
            if r == center[0] and c == center[1]:
                continue
            # 2. 存放邻居像素的xy位置，以及邻居像素的强度，用于后面计算权重的
            neighbors.append([r, c, pic[r, c, 0]])
    return neighbors

affinity_a函数

1）获取邻居像素的强度和中间像素的强度

2）计算强度的差值 $Y(r)-Y(s)$

3）计算强度的均方差 $\sigma$ ，可以直接用np.var计算

4）根据公式计算权重

5）更新权重，是经过加权之后的权重，最后记录权重

Copy
def affinity_a(neighbors, center):
    # 创建一个新的数组，存放权重，同时保留邻居像素的信息，因此可以直接copy数组neighbors
    nbs = np.array(neighbors)
    # 1. 获取邻居像素的强度和中间像素的强度
    sY = nbs[:,2] # 邻居像素的强度
    cY = center[2] # 中间像素的强度
    # 2. 强度差值
    diff = sY - cY 
    # 3. 计算均方差
    sig = np.var(np.append(sY, cY)) 
    if sig < 1e-6:
        sig = 1e-6
    # 4. 根据公式求权重
    wrs = np.exp(- np.power(diff,2) / (sig * 2.0))
    # 5. 加权求和，记得wrs是负数
    wrs = - wrs / np.sum(wrs) 
    nbs[:,2] = wrs # 记录权重
    return nbs

to_seq函数：用于根据像素位置x,y计算像素索引

Copy
# 创建索引
def to_seq(r, c, rows):
    return c * rows + r

计算b向量

由于矩阵A在计算过程中对邻居像素无差别计算权重（即没有去判断邻像素是否已上过色），所以b向量的计算也简单了很多，只要把已被上色的像素的U/V的值放在对应的索引位置即可

另外，在计算U和V只有b向量的差别，矩阵A都是权重矩阵，其计算依据的是强度Y，因此是一样的

Copy
b_u = np.zeros(size)
b_v = np.zeros(size)
idx_colored = np.nonzero(hhash.reshape(size, order='F'))
u = yuv[:,:,1].reshape(size, order='F')
b_u[idx_colored] = u[idx_colored]
v = yuv[:,:,2].reshape(size, order='F')
b_v[idx_colored] = v[idx_colored]

解方程组

利用scipy.sparse.linalg.spsolve求解方程组

Copy
ansU = sparse.linalg.spsolve(matA, b_u)
ansV = sparse.linalg.spsolve(matA, b_v)

转为RGB空间

同样可以利用colorsys进行转换

主函数

Copy
ansY = yuv[:,:,0].reshape(size, order='F')
ans = yuv_to_rgb(ansY,ansU,ansV)

yuv_to_rgb函数：利用colorsys进行转换

Copy
def yuv_to_rgb(cY,cU,cV):
    ansRGB = [colorsys.yiq_to_rgb(cY[i],cU[i],cV[i]) for i in range(len(ansY))]
    ansRGB = np.array(ansRGB)
    ans = np.zeros(yuv.shape)
    ans[:,:,0] = ansRGB[:,0].reshape(rows, cols, order='F')
    ans[:,:,1] = ansRGB[:,1].reshape(rows, cols, order='F')
    ans[:,:,2] = ansRGB[:,2].reshape(rows, cols, order='F')
    return ans

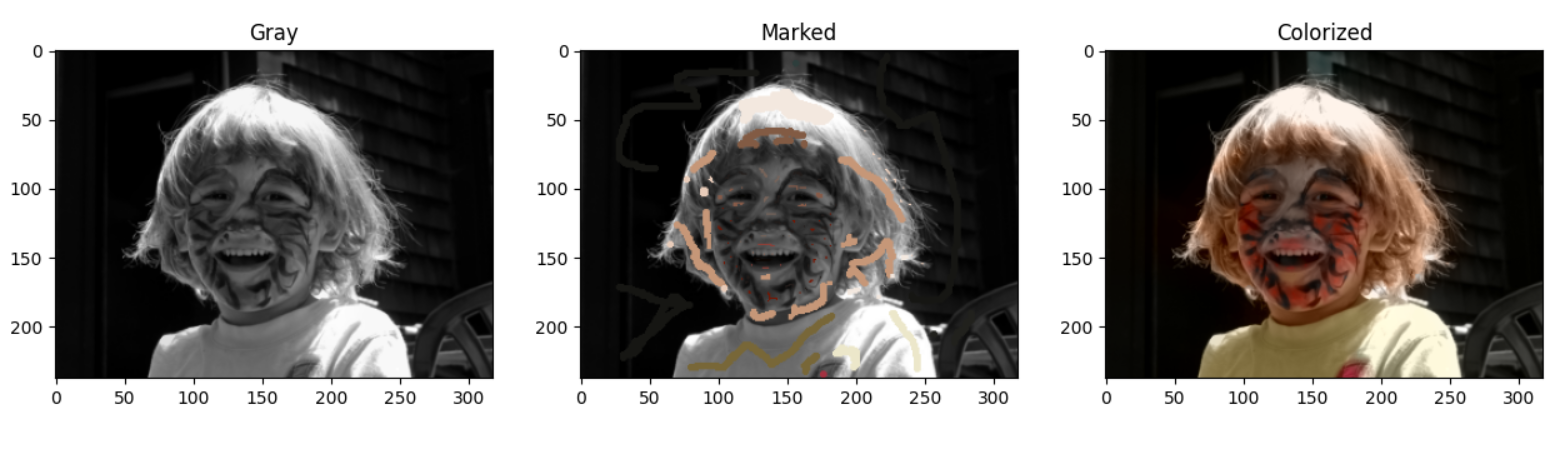
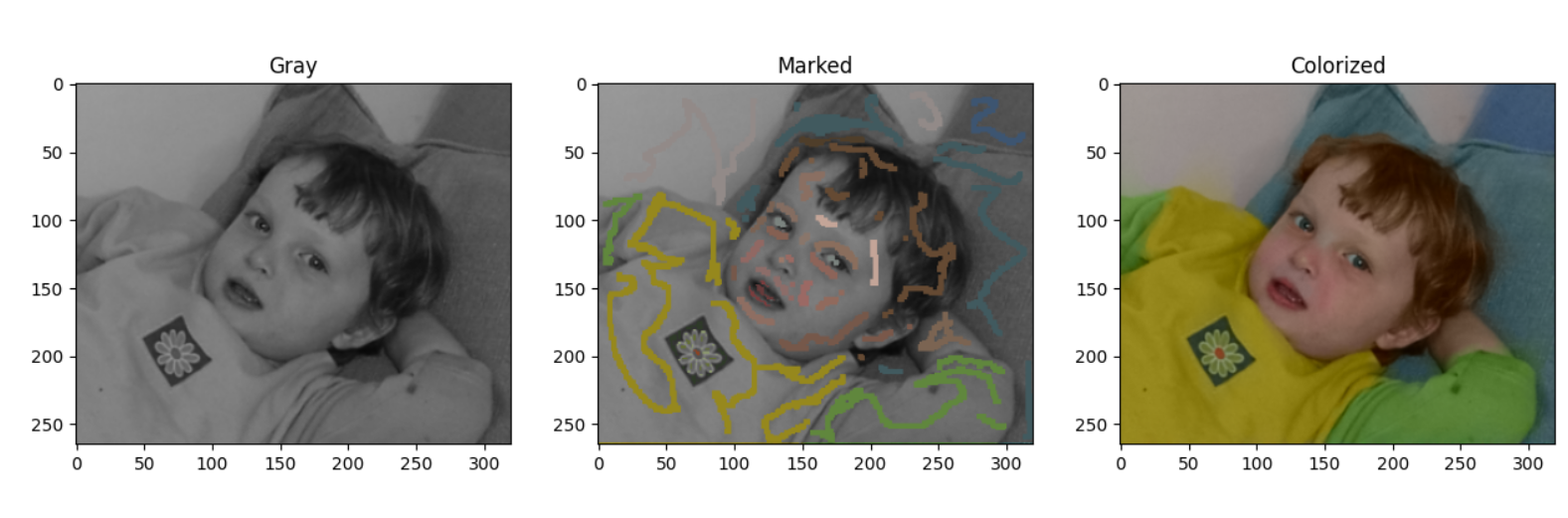
显示结果

利用matplotlib显示上色结果

Copy
fig = plt.figure()
fig.add_subplot(1,3,1).set_title('Gray')
imgplot = plt.imshow(src)
fig.add_subplot(1,3,2).set_title('Marked')
imgplot = plt.imshow(marked)
fig.add_subplot(1,3,3).set_title('Colorized')
imgplot = plt.imshow(ans)
plt.show();

6. 思考的问题#

为什么要用YUV？

YUV颜色编码采用的是明亮度和色度来指定像素的颜色。不像RGB颜色空间，是三个色域决定颜色，并且三者的决定程度是一样的，因此在上色时无法根据其中一个的相似性来决定整个像素的颜色。相反，YUV削弱了色度的决定性，加上了同样有很大决定性因素"明亮度"。通过时间上的相似”明亮度“以及空间上的相近”邻居距离“决定像素的颜色，我认为是更合理的。

为什么实现约束“像素r和相邻像素的s有相似的强度则有相似的颜色”，要最小化“r像素的颜色与相邻像素的加权颜色和”的差异？

我查阅了同样用到亲和函数的另外两篇论文，也有用到加权相似度最小的思想。但是是用在分割上，最佳分割结果可以导致被分割出来的一方各个点与另一方各个点的加权最小。使用加权的原因是更关注内部的紧密性。分割中体现的是只有分割出来的子集内部相似度（作为分母）足够大最终的相似度才会足够小。

在这里约束也利用到了相似度衡量距离，当Y(r)类似于Y(s)时较大，当两种强度不同时较小，因此权重衡量了强度的大小；并且利用了加权，确保内部的紧密性，避免因为某个像素权重过大而导致失衡吧。

参考文献#

读源码学算法之Colorization https://blog.csdn.net/u011426016/article/details/103427914
【计算机图形学】基础 - Colorization using Optimization https://blog.csdn.net/passer__jw767/article/details/126136158
Normalized Cuts and Image Segmentation https://blog.csdn.net/MTandHJ/article/details/120372214
Python标准库 colorsys --- 颜色系统间的转换 https://blog.csdn.net/m0_46653437/article/details/111831011
numpy中的方差、均方差、相关系数 http://www.360doc.com/content/20/0528/09/7669533_915078965.shtml

posted @ 2022-09-13 00:30 要兵长还是里维阅读(986) 评论(3) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 《Poisson Image Editing》论文理解与复现

· LIS模型之变形题 Python实现

· Python 图像处理实用指南：6~10

· PCSR：已开源，三星提出像素级路由的超分辨率方法 | ECCV 2024

· 【图像处理笔记】图像分割之阈值处理

阅读排行：
· 全程不用写代码，我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了，比商业数据库还牛
· .NET10 - 预览版1新功能体验（一）

公告

昵称：要兵长还是里维
园龄： 4年7个月
粉丝： 2
关注： 1

+加关注

2025年3月

日

一

二

三

四

五

六

要兵长还是里维

《Colorization Using Optimization》论文理解与复现

1. 导读#

2. 引言#

3. 技术贡献#

4. 方法介绍#

4.1 算法原理#

4.2 线性方程组求解#

5. 代码复现——基于python的opencv实现#

5.1 数据来源#

5.2 算法复现#

6. 思考的问题#

参考文献#

公告

搜索

常用链接

我的标签

随笔分类

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论