《线性代数的本质》笔记
零、引言
内容出自该链接
一、向量
1.1 什么是向量#
- 向量是空间中的箭头,决定一个向量的是它的长度和它所指的方向,可以在空间自由落脚
- 向量是有序的数字列表(此时二维向量代表的是列表长度为2)
- 向量只要保证两个向量相加以及数字与向量相乘是有意义的即可
1.2 向量的两个运算#
- 相加
- 定义:已知两个向量,为了把它们相加,我们平移第二个向量,使它的起点与第一个向量的终点重合,然后再画一个向量,从第一个向量的起点出发,指向第二个向量的终点
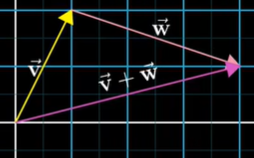
- 数学运算:向量加法就是把对应项相加
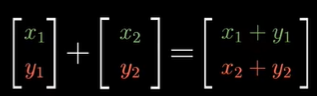
- 注意:
- 加法的定义基本是线性代数中唯一允许向量离开原点的情形
- 可以将相加这个运算看做粒子的运动,比如在原点移动了2,然后再移动5,这和在原点移动7是无异的
- 数乘
- 定义:一个向量乘一个数字n,意味着把这个向量“缩放”为原向量的n倍。如果这个数字是负数,说明这个向量需要先反向,然后再“缩放”
- 数学运算:向量数乘就是把对应项乘上对应数字
二、 线性组合、张成的空间与基
2.1 基向量 与 缩放向量并且相加#
- 向量的每个坐标都看作一个标量,用于缩放向量
- 以二维为例,在xy坐标系中,有两个特别的向量,一个指向正右方,长度为1,通常被称为“i-hat”/“the unit vector in the x-direction”;一个指向正上方,长度为1,通常被称为“j-hat”/“the unit vector in the y-direction”
- 向量[a,b]中,x坐标a是一个标量,将i-hat拉伸为原来的a倍;y坐标b将j-hat拉伸为b倍,这个向量是两个经过缩放的向量的和
- i-hat和j-hat被称为“基向量”
- 我们完全可以选择不同的基向量,并获得一个合理的新坐标系
2.2 线性组合#
- 定义:两个数乘向量的和被称为这两个向量的线性组合
- 注意:
- 在二维平面上,如果两个标量同时自由变化,考虑所有可能得到的向量:
- 两个向量指向不同方向时,是可以到达平面中的每一个点
- 两个向量恰好共线时,所产生的向量的终点都被限制在一条直线上
- 两个向量都是原点时,只有原点
2.3 张成的空间#
- 定义:所有可以表示为给定向量线性组合的向量的集合被称为给定向量张成的空间
The "span" of and is the set of all their linear combinations. So and let a and b vary over all real numbers
- 注意
- 在三维空间里,两个指向不同方向的向量张成的空间是一个经过原点的平面
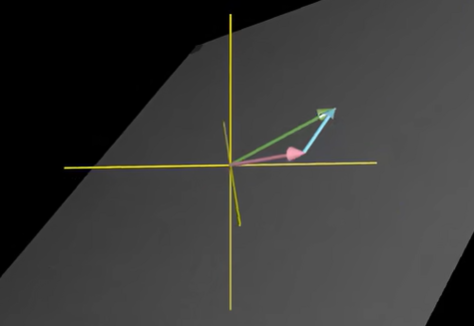
- 如果两个向量恰好共线时,即一组向量至少有一个是多余的,没有对张成空间做出任何贡献
2.4 线性相关#
- 定义:
- 当有多个向量时,可以移除其中一个而不减小张成的空间,这种情况称之为“线性相关”
- 另一种表述:其中一个向量可以表示为其他向量的线性组合,因为这个向量已经落在其他向量张成的空间之中
- 注意:
- 比如,在二维空间中有两个向量,如果共线,则可以说他们“线性相关”
2.5 线性无关#
- 定义:所有向量都给张成的空间增添了新的维度,则称它们为“线性无关”
- 另一种表述: for all values of a and b
- 基的严格定义:向量空间的一组基是张成该空间的一个线性无关向量集
三、矩阵与线性变换
3.1 线性变换(Linear transformation)#
- “变换”本质上是“函数”的一种说法,指的是接收一个向量并输出一个向量的变换
- “线性”是什么意思?
- 如果一个变换具有以下两个性质,我们就称它是线性的:
- 直线在变换后仍然保持为直线,不能有所弯曲(Lines remain lines)
- 原点必须保持固定(Origin remains fixed)
- 线性变换应是“保持网格线平行且等距分布”
- 如何用数值描述线性变换?
- 只需记录两个基向量i-hat和j-hat变换后的位置(因为所有向量都是i-hat和j-hat的一个线性组合,变换后也是相同的线性组合)
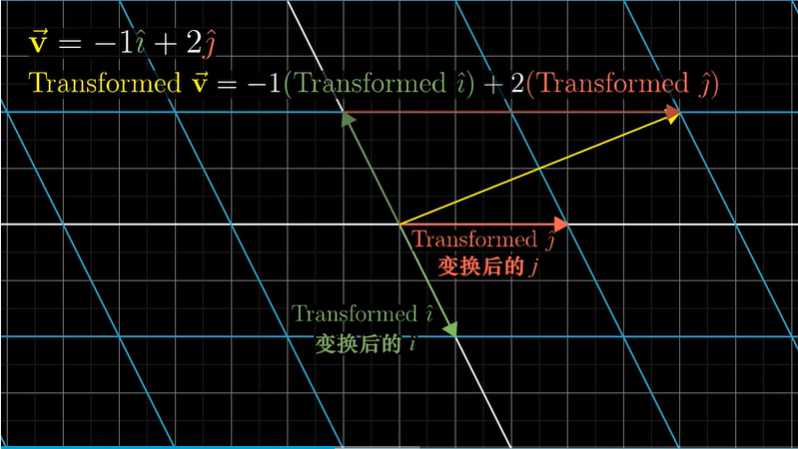
- 对于变换后的基向量,通过判断坐落在变换前坐标的位置可以得到变换后的坐标
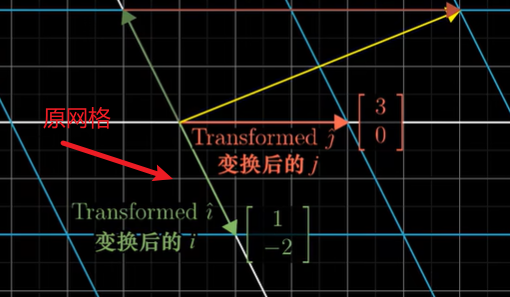
- 只要记录了变换后的i-hat和j-hat,就可以推断出任意向量在变换后位置(一个线性变换仅由)

- 通常将这些坐标包装在一个2*2的矩阵中,可以理解为两个特殊的向量,变换后的i-hat和j-hat各作为矩阵的列
- 计算方法:
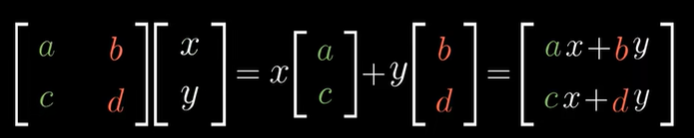
- 常见的线性变换矩阵
- 逆时针旋转90度
- 错切
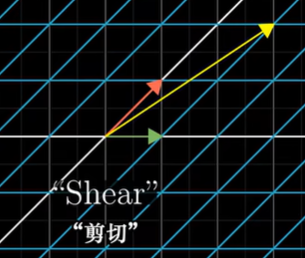
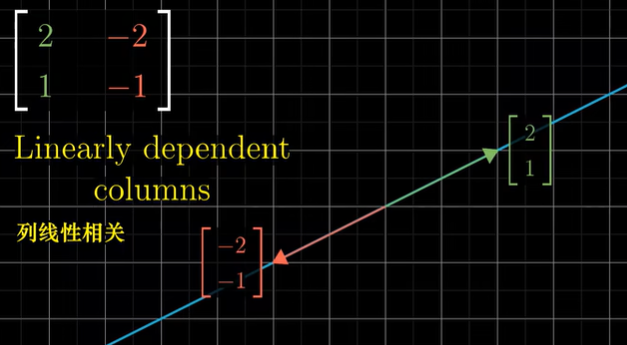
- 列线性相关
- 如果变换后的i-hat和变换后j-hat是线性相关,那这个线性变换将整个二维空间挤压到它们所在的一条直线上
**总的来说,线性变换是将向量作为输入和输出的一类函数,也可以将线性变换看作对空间的挤压伸展,它保持网格线平行且等距分布,并且保持原点不变 **
四、矩阵乘法与线性变换复合
1. 复合线性变换#
- 有些时候如果想描述这样一种作用:一个变换之后再进行另一个变换(如先旋转再剪切),这种新的线性变换通常被称为前两个独立变换的“复合变换”。
- 复合变换也可以用一个矩阵来完美描述

2. 矩阵乘法和复合变换的关系#
从上面可以看出,复合矩阵捕捉到了剪切矩阵和旋转矩阵的总体效应,实际上也是前两个矩阵的乘积,如图:
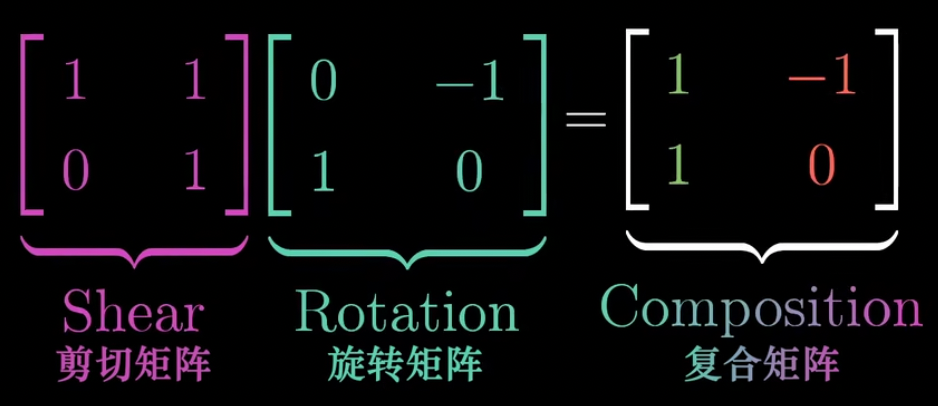
因此,这两个矩阵相乘有着几何意义,即两个线性变换相继作用。
- 相继作用的顺序是从右往左读的,这起源于函数的记号,因为我们将函数写在变量左侧
- 矩阵相乘的计算公式可以这么理解:
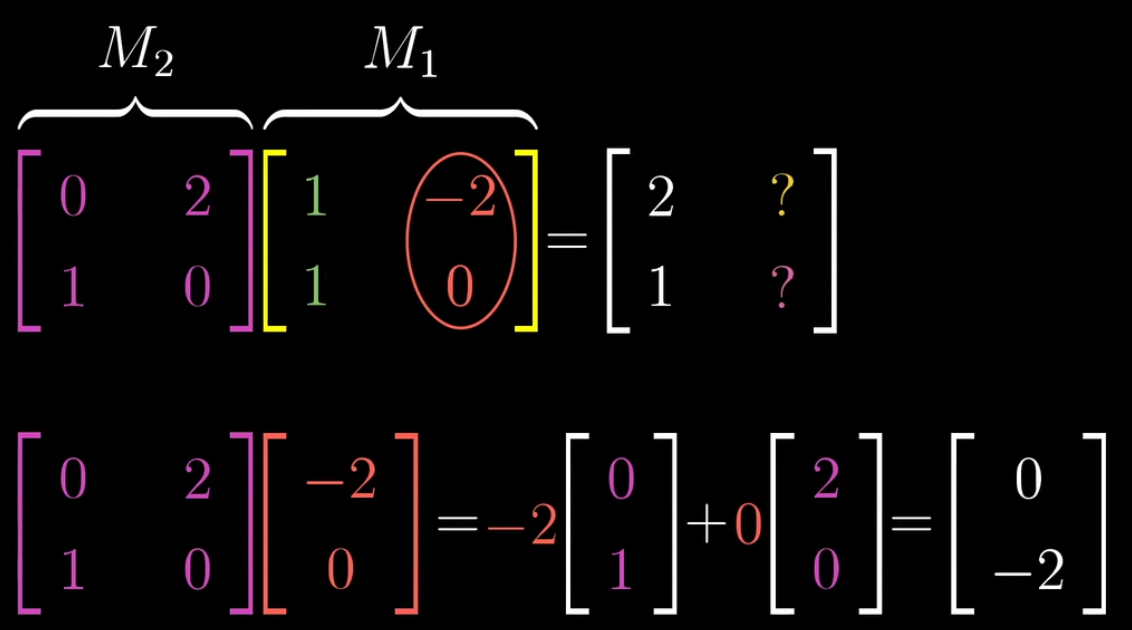



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· DeepSeek在M芯片Mac上本地化部署