字符串之 KMP 字符串前缀哈希

一、KMP--字符串匹配算法#

1.1 什么是KMP#

• 三个提出者名字首字母组成
• 解决的问题：字符串匹配问题
  • 给定一个文本串s，以及一个模板串p，求模板串是否出现在文本串中，是的话出现在哪个位置

1.2 字符串匹配的暴力做法#

• 两层遍历：O(mn)

• 缺点

  • 每当匹配不成功，pat的j都是回溯到最开头（向右滑动一位），从头开始匹配
    • 让pat串向后移动就是j指针回溯
  • 每当匹配不成功，txt的指针也要回溯，从下一位开始匹配

  能不能做到：txt串的指针一直都是向前走的，而不让pat移动到最开头，让它移动到一个地方，从那个地方继续和i匹配（即利用已经得到的“部分匹配”的结果）？

1.3 KMP相关概念#

• s[ ] : 文本串，较长字符串
• p[ ]：模式串，较短字符串
• 非平凡前缀：包含首字母，不包含尾字母的所有子串
• 非平凡后缀：包含尾字母，不包含首字母的所有子串
• 最长相等前后缀：前缀和后缀 的 最长共有元素 的长度
• next[ ]：存储每一个下标对应的最长相等前后缀

1.4 KMP基本思想#

在每次失配时，不是把p串往后移一位，而是把p移动至下一次可以和前面部分匹配的位置，这样就可以跳过大多数的失配步骤。

每次p串移动的步数通过查找next[ ]数组确定的。

时间复杂度O(m+n)

1.5 next数组的含义#

• 含义

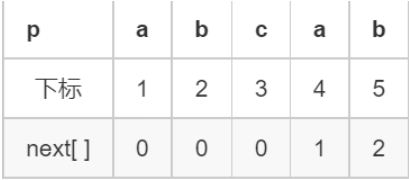
  next[ j ]表示p[ 1, j ]串中前缀和后缀相同的最大长度

  next[j]表示为 p[1, next[j]]= p[j - next[j] + 1, j]

  

• 模拟

  next[1] = 0：前缀集合为空，后缀集合为空

  

1.6 匹配的思路#

KMP算法分两步：求next数组、匹配字符串

对于匹配字符串，其思路为：

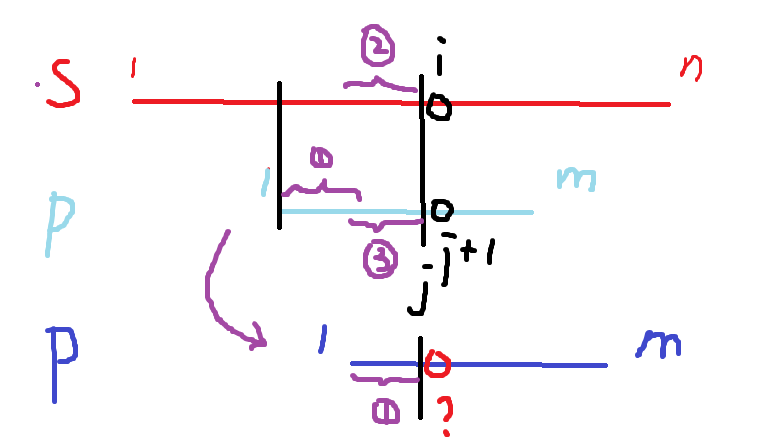
s串和p串都人为规定为下标从1开始

i从1开始，j从0开始，每次将 s[i]和 p[ j + 1]比较

if s[i] != p[j + 1]

​ 不断回溯 j串，不只移动1格，而是直接移动到下次能匹配的位置（由 j = next[j] 完成）

if s[i] == p[j + 1]

​ 匹配 p串的下一位与 s串的下一位

直到 j == m匹配成功，即 p串最后一个元素 p[m]与 s相配了

Copy
for(int i=1, j=0; i<=n; ++i)
{
        while(j && s[i]!=p[j+1]) j = ne[j];
        //如果j有对应p串的元素， 且s[i] != p[j+1], 则失配， 移动p串
    	//用while是由于移动后可能仍然失配，所以要继续移动直到匹配或整个p串移到后面（j = 0)

        if(s[i]==p[j+1]) ++j;
        //当前元素匹配，j移向p串下一位
        if(j==m)//满足匹配条件
        {
                //匹配成功，进行相关操作
                printf("%d ",i - m + 1);//比如返回匹配成功的起始位置       
                j = ne[j];//继续匹配下一个子串
        }
}

• 思考

  • j 回溯到 0 代表什么？

    模式串已经没有一个字母能匹配了，要从第一个开始匹配

  • 为什么i和j要相差一位？

    与next[]含义有关

  • 为什么最后j=m匹配完了，j还要回溯？

    为了s继续匹配下一个p串

1.7 求next数组#

next数组的求法是通过模板串自己与自己 进行匹配操作得出来的（代码和匹配操作几乎一样）。

关键：每次移动i前，将i前面已经匹配的长度记录到next数组中

Copy
void get_next()//核心是求模式串p的next数组(记住next数组是相对于模式串而言的)
{
        for(int i=2, j=0; i<=m; ++i)//i从2开始,因为ne[1]=0,无需计算
        {
                while(j && p[i]!=p[j+1]) j = ne[j];
                if(p[i]==p[j+1]) ++j;//此时匹配到了前后缀相等
                ne[i] = j;//赶紧记录下来
        }
}

1.7 板子#

Copy
#include<iostream>
#include<cstring>

using namespace std;
const int M = 1e5+10, N = 1e6+10;
int m, n;
char p[M], s[N];
int ne[M]; 

int main()
{
        cin>>m>>p+1>>n>>s+1; //人为规定从1开始！！

        for(int i=2, j=0; i<=m; ++i)
        {
                while(j && p[i]!=p[j+1]) j = ne[j];
                if(p[i]==p[j+1]) ++j;
                ne[i] = j;
        }
    
        for(int i=1, j=0; i<=n; ++i)
        {
                while(j && s[i]!=p[j+1]) j = ne[j];
                if(s[i]==p[j+1]) ++j;
                if(j==m)
                {
                        printf("%d ", i-m);
                        j = ne[j];
                }
        }
        return 0;
}

1.8 模板题#

链接在此

Copy
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

using namespace std;
const int M = 1e6+10, N = 1e6+10;
int m, n;
char p[M], s[N];
int ne[M]; 

void get_next()
{
        for(int i=2, j=0; i<=m; ++i)
        {
                while(j && p[i]!=p[j+1]) j = ne[j];
                if(p[i]==p[j+1]) ++j;
                ne[i] = j;
        }
}

int main()
{
        cin>>s+1;
        cin>>p+1;
        n = strlen(s+1);
        m = strlen(p+1);
        get_next();
        for(int i=1, j=0; i<=n; ++i)
        {
                while(j && s[i]!=p[j+1]) j = ne[j];
                if(s[i]==p[j+1]) ++j;
                if(j==m)
                {
                        printf("%d\n", i-m+1);
                        j = ne[j];
                }
        }
        for(int i=1; i<=m; ++i){
            printf("%d ",ne[i]);
        }
        return 0;
}

二、字符串前缀哈希#

2.1 思想#

字符串哈希值：将字符串映射为数字形式

给定一个字符串，用一个数组存放字符串前i个字母的哈希值

2.2 定义字符串的hash值#

1. 将字符串看成P进制数，字母上的每一位看成P进制数上的每一位数字，再转换为十进制数

   

2. 转换成的数字可能会非常大，可以将其%Q，映射到（0~Q-1）的数

3. 根据经验值，P取131或13331冲突率会很低，而Q取$2^{64}$

   1. mod Q 可以等价与把存放哈希值的数组h[]声明为unsigned long long

2.3 应用#

求得任意一个区间的字符串的哈希值——询问某两个区间的子串是否相同/快速判断两个字符串是否相等

1. 根据定义分别求出hash[i]:

   $hash[1]=s1$

   $hash[2]=s1∗p+s2$

   $hash[3]=s1∗p^2+s2∗p+s3$

   $hash[4]=s1∗p^3+s2∗p^2+s3∗p+s4$

   $hash[5]=s1∗p^4+s2∗p^3+s3∗p^2+s4∗p+s5$

2. 现在我们想求s[3,4]（即s3s4）的hash值，不难得出为s3∗p+s4。并且从上面观察，如果看hash[4]−hash[2]并将结果中带有s1,s2系数的项全部消掉，就是所求。

3. 但是由于p的阶数，不能直接消掉，所以问题就转化成，将hash[2]乘一个关于p的系数，使得高位对齐。这样在在作差的时候可以将多余项消除，从而得到结果。

   eg. 1234 - 1200 = 34

$h[L,R]=h[R]-h[L-1]*P^{R-L+1}$

2.4 模板#

Copy
const int P = 131;
const int MAXN = 1e5 + 5;
typedef unsigned long long ULL;
ULL h[MAXN], p[MAXN]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
char str[MAXN];

// 初始化
void init(int n) {
    p[0] = 1;
    for (int i = 1; i <= n; i ++ ) {
        h[i] = h[i - 1] * P + str[i];
        p[i] = p[i - 1] * P;
    }
}

// 计算子串 str[l ~ r] 的哈希值
ULL get(int l, int r) {
    return h[r] - h[l - 1] * p[r - l + 1];

2.5 模板题#

链接在此

Copy
#include<iostream>
#include<cstring>
using namespace std;
typedef unsigned long long ULL;
const int maxn=1e6+5;
const int P=131;
char s[maxn],str[maxn];
ULL h[maxn],p[maxn];
ULL get(int l,int r)
{
    return h[r]-h[l-1]*p[r-l+1];
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        scanf("%s",str + 1);
        scanf("%s",s + 1);
        int n = strlen(s + 1);
        int m = strlen(str + 1);
        p[0] = 1;
        ULL h_str = str[1];
        for(int i = 2; i <= m; i++)
        {
            h_str = h_str * P + str[i];
        }
        for(int i = 1; i <= n; i++)
        {
            h[i] = h[i - 1] * P + s[i];
            p[i] = p[i - 1] * P;
        }
        int ans=0;
        for(int i = 1; i + m - 1 <= n; i++)
        {
            if(h_str == get(i, i + m - 1))
                ans++;
        }
        printf("%d\n",ans);
    }
	return 0;
}

参考文献#

labuladong的算法小抄

Acwing yxc大神的基础课