并查集问题
一、概述
1.并查集是一种用于解决所谓的动态连通性问题的算法。
2.使用算法解决问题的第一步是建立问题模型,找出解决该问题大体上所需要的基本操作
二、动态连通性问题
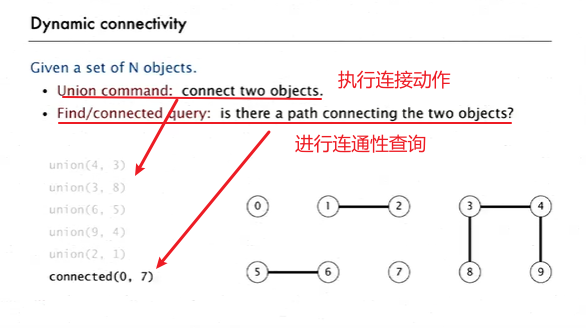
任务:对于给定的对象集合高效地实现“并”与“查”这两个命令。
PS:本次学的算法不会给出一条具体的路径,只能回答这样的问题:是否存在一条路径
1. 连通性必须满足的抽象性质
- 每个对象都能连接到自己
- 对称性
- 传递性
2. 连通分量(Connected components)
- 含义:maximal set of objects that are mutually connected---互相连接的对象的最大集合
- 算法中通过维护连通分量来获得效率,并通过连通分量来高效地应答接收到的请求
3. 如何通过连通分量来实现查找和合并操作?
- 查找:检查两个对象是否在相同的分量中
- 合并:将包含两个对象的分量替换为其并集
三、Quick find--解决动态连通性问题算法的第一种实现
1. data structure
- quick find是一种用于求解此类问题的贪心算法,用来支持这个算法的数据结构是数组。
- p和q是连通的当且仅当数组中的项是一样的。
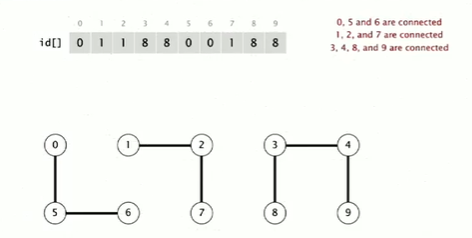
实现查找:检查p和q是否有相同的id
实现合并:将所有与给定对象之一相同的id对应的项变为另一给定对象对应的项。--操作会因对象数目很大时出现些问题,因为有很多值要改变
2. 代码实现
首先先设置id数组的每一项都等于它的索引,说明所有的对象都是独立的
当进行合并操作时(如合并3和4),将所有与第一个id项(3对应的项)相同的元素变为第二个id的项---记录两个id项,然后遍历整个数组,满足与第一个id项相同的,就将其改为第二个id项
3.算法分析
- 时间复杂度:O(N^2)

四、Quick Union--避免计算直到不得不进行计算
1.data structure
- 大小为N的数组
- 数组的含义:把数组看作一组树即一片森林,数组中的每一项包含它在树中的父节点,即id[i]是i的父节点
- i的根节点是id[id[id...id[i]...]]]

实现查找:两个对象的根节点是否相同
实现合并:将P的根节点id记录值设为Q的根节点ID记录值,即将P的树指向Q
2. 代码实现
首先对数组进行初始化(同quick find)
当进行合并操作时(如union(4,3)),即将4和3放在同一个分量中,就要将包含第一个对象的分量的根节点变成包含第二个对象的分量的根节点的一个子节点
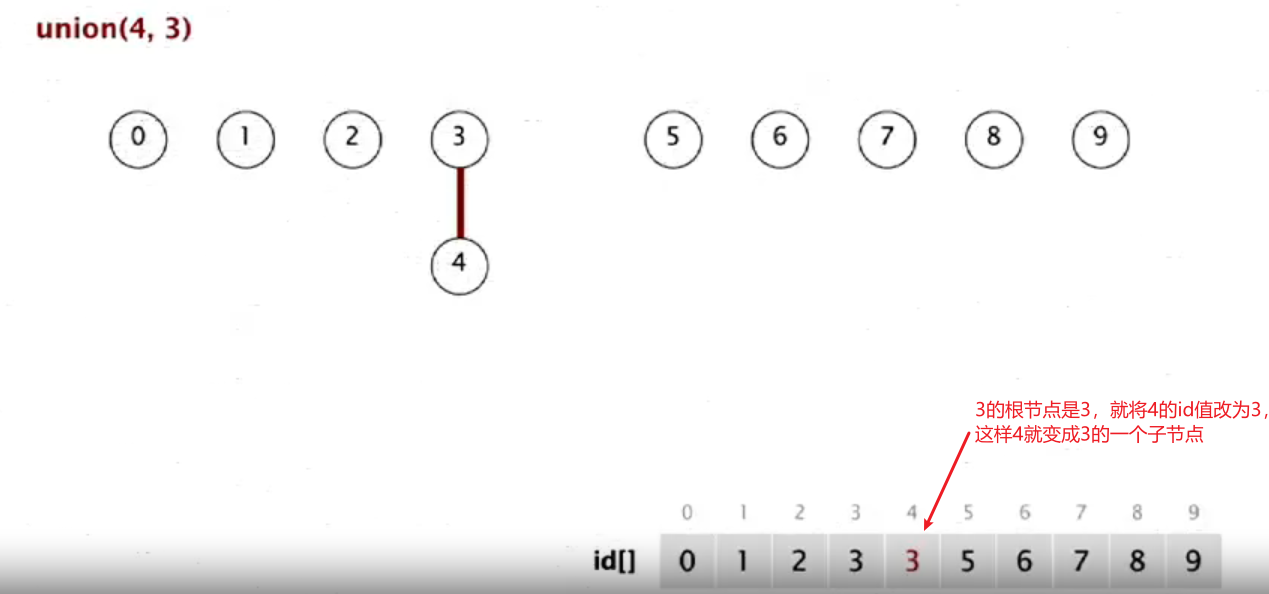
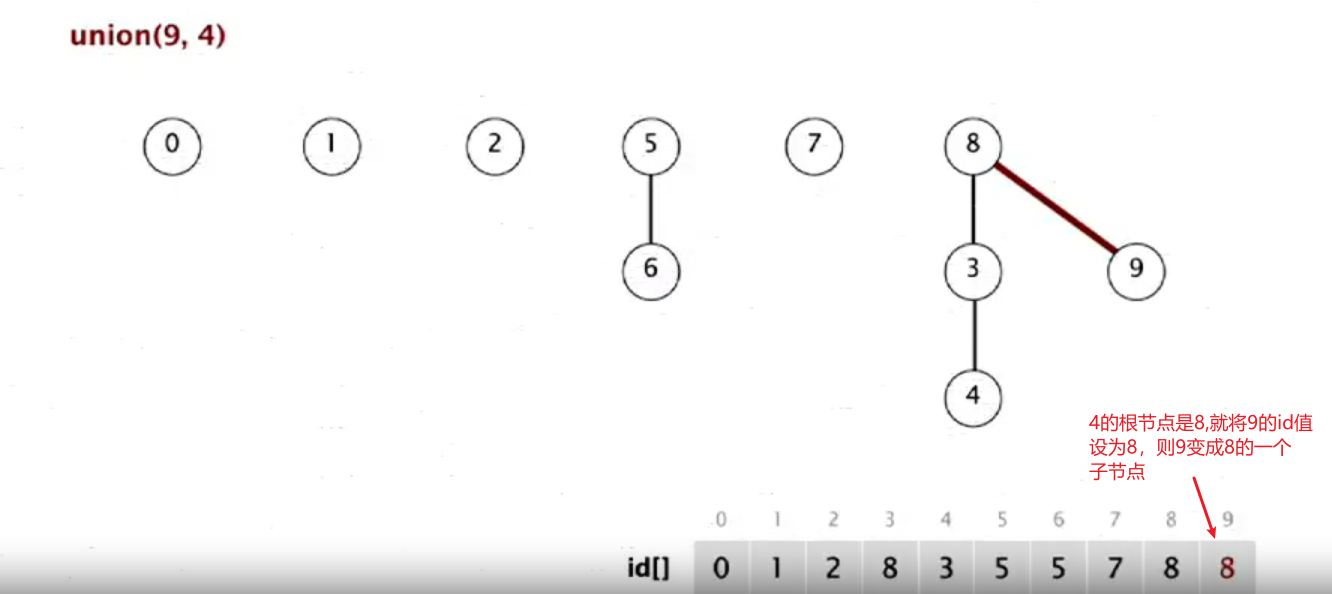
具体代码实现(注意其中如何找根节点这个操作)

3. 算法分析
时间复杂度:O(N^3) --初始N + 查找N + 合并N
与快速查找相比是另一种慢,如果树太高时,要回溯整棵树,就会很慢
五、改进1--带权快速合并
1. 目的:在实现快速合并算法的时候执行加权操作避免得到很高的树
如一棵大树合并一棵小树,就可以避免将大树放在下面,因为那将导致更高的树。
2. 加权如何实现?
跟踪每棵树中对象的个数,然后通过确保将小树的根节点作为大树的根节点的子节点来维持平衡。
与前面最开始的算法相比改进点在于:合并看的不是参数的顺序,而是参数所在的树的权
3. data structure
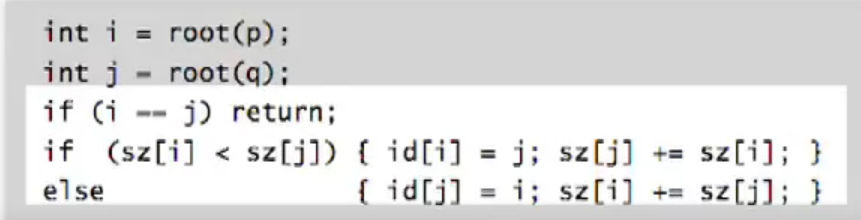
两个数组id[]和sz[],其中一个与quick union的一样,另一个给出以该对象为根节点的树中的对象个数,在合并操作中会维护这个数组。
4.算法的实现
查找操作同quick union,只需检查根节点是否相同
合并操作时,要先检查树的大小,然后将小树的根节点连接到大树的根节点上,在改变id记录值后还要维护数组,如果i变为j的子节点,则要给j的树的大小加上i的树的大小。
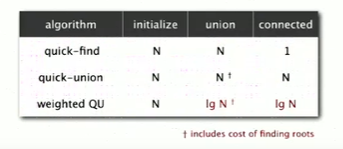
5.算法分析
- 时间复杂度--时间与树的深度成正比
PS:任意节点的深度上限是以2为底的对数。
证明这个问题在于要理解节点的深度何时增加了。当节点x所在树的大小小于等于另一棵树的大小时,节点的深度才会+1(因为所在的树成子树了)。而此时包含x节点的树在合并后大小至少会翻倍。因此,包含x的树的大小最多可以翻N次倍。而从1开始,翻倍lgN次,就会得到N。故操作需要的时间与lgN成正比。
六、改进2--路径压缩
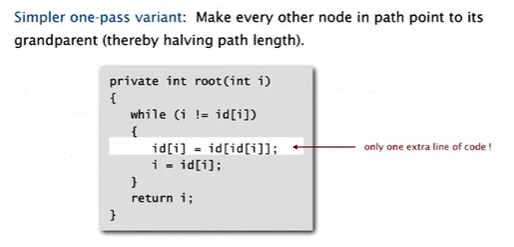
1.做法:将每个节点都指向根节点,那查找就不用一层一层访问了。
2.具体实现
回溯一次路径找到根节点,再回溯一次将树展平。
七、应用模型--渗滤
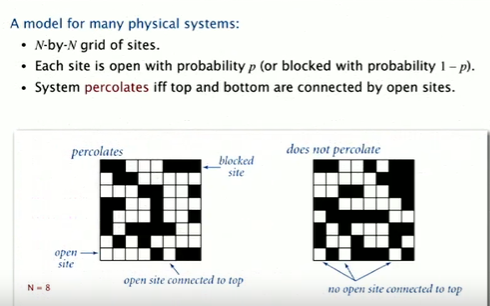
1.定义:一个nxn的方形网格,小方格叫做位。每个位是开放的概率为p 如图中为白色方格。位是闭合的概率为1-p。如果顶端和底端被开放的位连通,则称这个系统是渗滤的。如图左是渗滤的,图右不是。
2.理解:当闭合概率大小会影响是否渗滤。但存在一个值当N非常大时p小于该值时 系统基本肯定不是渗滤的,如果大于该值基本一定会渗滤。问题就是那个值是多少。而要实现那些仿真必须使用快速并查集算法。
3.做法
首先将整个网格初始化为闭合的,全是黑色的,然后随机加上开放的位,每次加上一个开放位后,检查是否使系统变得渗滤的。持续这个过程直到系统变得是渗滤的
PS1:再稍微看一些使用动态连通性模型的细节。很显然,对应每个位我们要创建一个对象,然后赋予他们一个名字,像这里表示的从0到N^2-1。
PS2:如果检查最下面一行中是否有位、与最上面一行任何一个位连通,并使用并查集来完成。但这么做的问题在于这是一个暴力算法,需要平方时间。
改进:在顶端和底端各加一个虚拟位,那么想知道系统是否渗滤时,只需要检查虚拟顶端位和虚拟底端位是否连通,那么我们要怎么对开放新位建模呢?开放一个位我们只需要将它和它周围的开放位连通 所以需要调用几次合并操作。