Hanoi问题及其相关快速算法
Hanoi问题
抽象
hanoi(n,x,y,z)
step1: hanoi(n-1,x,z,y)
step2:move(x,z)
step3:hanoi(n-1,y,x,z)
递归部分实现代码
void hanoi(int n, char x, char y, char z){
if(n==1){ // 递归出口
move(x,z);
}
else{
hanoi(n-1,x,z,y);
move(x,z);
hanoi(n-1,y,x,z);
}
}
实例
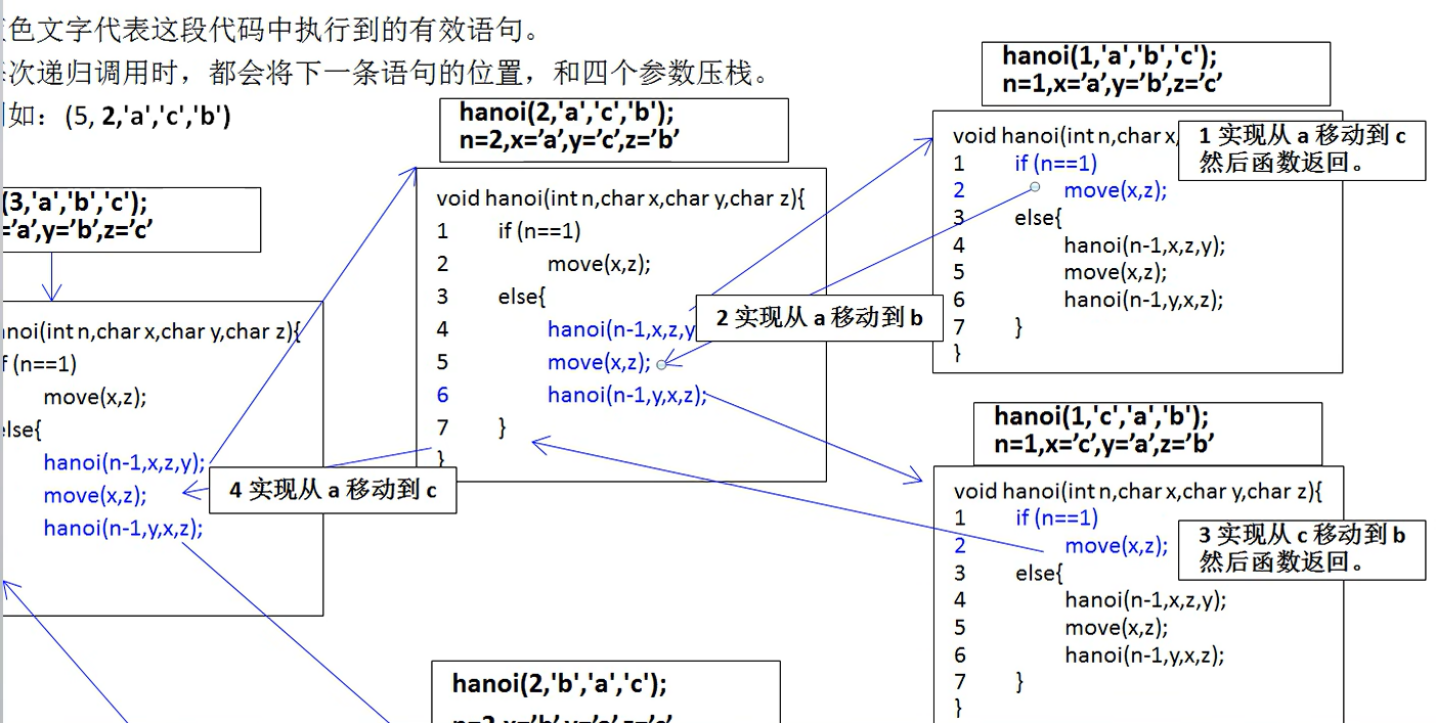
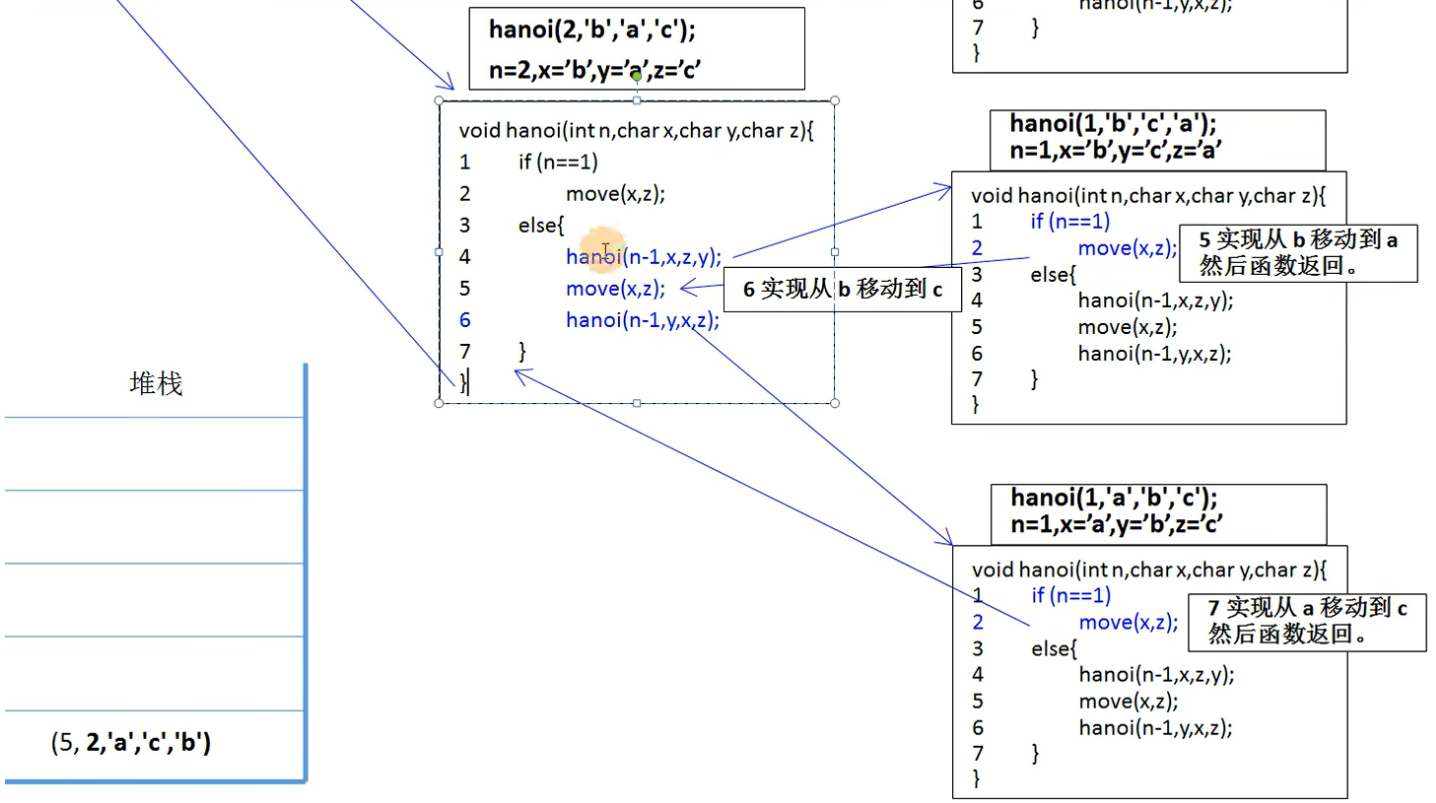
hanoi(3,'a','b','c')
1.保留入栈line5：n=3 x='a' y='b' z='c'
2.调用hanoi(2, 'a','c','b')
3.保留入栈line5：n=2,x='a',y='c',z='b'
4.调用hanoi(1,'a','b','c')
5.n==1,x->z,namely,a->c
6.返回(3)line5,同时(3)释放出栈,现场恢复，执行move(x,z),a->b
此时hanoi(2,'a','c','b')调用仍未结束
7.调用前保留入栈line7：n=2,x='a',y='c',z='b'
8.调用hanoi(1,'c','a','b')
9.n==1,move(x,z),namely,c->b
此时hanoi(2,'a','c','b')调用结束，(7)释放出栈恢复现场
语句执行完毕,(1)出栈
10.执行下一条语句move(x,z),namely,a->c
11.保留入栈line7:n=3,x='a',y='b',z='c'
12.调用hanoi(2,'b','a','c')
13.保留入栈line5：n=2,x='b',y='a',z='c'
14.调用hanoi(1,'b','c','a')
15.n==1,move(x,z),namely,b->a
16.返回(13)line5，同时(13)释放出栈
17.执行下一条语句move(x,z),namely,b->c
18.保留入栈line7:n=2,x='b',y='a',z='c'
19.调用hanoi(1,'a','b','c')
20.n==1,move(x,z),namely,a->c
此时hanoi(2,'b','a','c')调用结束，(18)释放出栈恢复现场
语句执行完毕,(11)出栈
18.hanoi(3,'a','b','c')调用结束
递归轨迹
普通hanoi公式
3个柱子 n个盘子 移动步数2^n-1
int:10^9 long long:10^18 超过数量级采用高精度算法
高精度算法:借助数组逐位处理
加法
#include<bits/stdc++.h>
using namespace std;
char s1[505],s2[505];
int a[505],b[505],c[505];
int main(){
int la.lb,lc;
scanf("%s",s1);
scanf("%s",s2);
//获取长度
la=strlen(s1);
lb=strlen(s2);
//逆置 方便各位对齐
for(int i=0;i<la;i++){
a[la-i]=s1[i]-'0';
}
for(int i=0;i<lb;i++){
a[lb-i]=s2[i]-'0';
}
lc=max(la,lb)+1;
//高精度加法
for(int i=1;i<lc;i++){
c[i]+=a[i]+b[i];
c[i+1]=c[i]/10;
c[i]=c[i]%10;
}
//当长度大于0 若有前导0 则删除
if(c[lc]==0&&lc>0) lc--;
//逆置输出
for(int i=lc;i>0;i--){
cout<<c[i];
}
return 0;
}
减法
#include<bits/stdc++.h>
using namespace std;
char s1[10090],s2[10090],s3[10090];
int a[10090],b[10090],c[10090];
int flag;
bool compare(char *s1,char *s2,int u,int v){
if(u!=v) return u>v;
for(int i=0;i<u;i++){
if(s1[i]!=s2[i])
return s1[i]>s2[i];
}
return true;
}
int main(){
int la,lb,lc;
scanf("%s",s1);
scanf("%s",s2);
la=strlen(s1);
lb=strlen(s2);
if(!compare(s1,s2,la,lb)){
flag=1;
strcpy(s3,s1);
strcpy(s1,s2);
strcpy(s2,s3);
}
//需要再次获取以确认大数-小数对应的长度
la=strlen(s1);
lb=strlen(s2);
//逆置 方便各位对齐
for(int i=0;i<la;i++){
a[la-i]=s1[i]-'0';
}
for(int i=0;i<lb;i++){
b[lb-i]=s2[i]-'0';
}
lc=max(la,lb);
//高精度减法
for(int i=1;i<=lc;i++){
if(a[i]<b[i]){
a[i+1]--;
a[i]+=10;
}
c[i]=a[i]-b[i];
}
//相对于加法 此处lc=max(la,lb) 循环删除前导0
while(c[lc]==0&&lc>1) lc--;
if(flag){
cout<<"-";
}
//逆置输出
for(int i=lc;i>0;i--){
cout<<c[i];
}
return 0;
}
乘法
#include<bits/stdc++.h>
using namespace std;
char s1[2005],s2[2005];
int a[2005],b[2005],c[2005];
int main(){
int la,lb,lc;
scanf("%s",s1);
scanf("%s",s2);
la=strlen(s1);
lb=strlen(s2);
lc=la+lb;
//逆置 方便各位对齐
for(int i=0;i<la;i++){
a[la-i]=s1[i]-'0';
}
for(int i=0;i<lb;i++){
b[lb-i]=s2[i]-'0';
}
//高精度乘法
for(int i=1;i<=la;i++){
for(int j=1;j<=lb;j++){
c[i+j-1]+=a[i]*b[j];
c[i+j]+=c[i+j-1]/10;
c[i+j-1]%=10;
}
}
//循环删除前导0 lc>1 namely 0*10=0
while(c[lc]==0&&lc>1) lc--;
//逆置输出
for(int i=lc;i>0;i--){
cout<<c[i];
}
return 0;
}
二次幂
#include<bits/stdc++.h>
using namespace std;
int n;
int a[15005];
int main(){
a[1]=1;
cin>>n;
int len=1;
for(int i=1;i<=n;i++){//a[]*2
int t=0;
//高精度乘以一位数
for(int j=1;j<=len;j++){
a[j]=a[j]*2+t;
t=a[j]/10;
a[j]%=10;
}
//t为进位 只能有一位
if(t>0) a[++len]=t;
}
for(int i=len;i>=1;i--){
if(i==1){
cout<<a[i]-1;
}
else{
cout<<a[i];
}
}
return 0;
}
快速幂
复杂度：O(log b)
#include<bits/stdc++.h>
using namespace std;
long long a,b,c;
int main(){
cin>>a>>b>>c;
a%=c;
long long ans=1;
while(b){
// b is odd or even?
if(b&1){
ans=(ans*a)%c;
}
a=(a*a)%c;
// b/2
b>>=1;
}
cout<<ans<<endl;
return 0;
}
