10.11 模拟赛（云智计划 模拟测#26）
S---【云智计划】---6月23日---模拟测#26 div1【补题】 - 比赛 - 梦熊联盟 (mna.wang)
S---【云智计划】---6月23日---模拟测#26 div2【补题】 - 比赛 - 梦熊联盟 (mna.wang)
复盘
A。看到 \(n\) 为偶数思路秒出。10min 过样例。
B。好像不太会做啊。模拟了样例 2，猜出了一个很优的贪心重排方法。然后尝试了两三种答案的表达方式。很快得到了正解。估计 30min 时做完了。
C。模数不是质数所以逆元不好做？肯定排除掉前缀和等带除法的做法。
不能除，只能从某个位置开始，向一边慢慢拓展，这样只会用到乘。但往只一边扩展的复杂度……
我可以往两边扩展。cdq 分治。然后做完了。
9:00 写完，一边过大样例（！！！！）。非常惊讶但是看上去大样例很强就先往后做了。
D。一眼打表找规律题。先写爆搜。
样例没过？dfs 每个位置的值后，把所有合法区间按右端点排序然后贪心选不对吗？算了反正数据量很小 check 里面再写个爆搜吧。这样复杂度是 \(2^{n+n^2}\) 的。
然后过了样例。但是打表速度相当之慢（\(n=7,k\ge5\) 就跑不了了）。
哦哦哦我的贪心里有个 cnt 写成了 n。改过来过了样例。这下 \(n, k\le 8\) 的表就打出来了。复杂度 \(2^nn^2\)。
瞅规律！未果。但是这个贪心好像可以写成一个更优美的形式：每次找到一个最短的包含起始位置的最短的满足 \(\gcd = 1\) 的区间，然后把这个区间删掉。持续这样操作跟刚才的贪心是一模一样的。这样复杂度 \(2^nn\)。跑出来了 \(n, k \le 9\) 的表。
继续瞅规律！显然没找到。但是这样贪心好像就可以设计 DP 了。
但是我没学过 DP 所以我还是不会。
E。前 \(40\) 分极易，写写写。想不出 \(P\) 是质数怎么做（其实是 dsu on tree，但我不会（？））。
然后结束了。没有挂分。\(100+100+100+20+40\)。
总结
好的：
- 5 道题这么多分没有挂真的很强。
- cdq 分治没调直接过。
不足：
- DP 太菜。不会设状态。
题解
A. 弟德巴赫
不是这个题目名有点牛。
因为 \(n\) 是偶数，所以 \(a^2,b^2,c^2\) 中必有 \(1\) 或 \(3\) 个偶数。
平方后奇偶性不改变（我放个 div3 B 的相关链接是不是不太正常）。所以 \(a, b, c\) 中必有 \(1\) 或 \(3\) 个偶数。
因为 \(a, b, c\) 都是质数且互不相同，而偶质数只有一个 \(2\)，所以 \(a, b, c\) 中必有一个 \(2\)，另外两个是偶数。
于是问题变成了，求有多少奇质数 \(b, c\) 满足 \(b^2+c^2=n-2^2\)。因为 \(n \le 10^{10}\)，所以 \(b,c \le 10^5\)。枚举其中一个然后做差求出另一个，判断是否合法即可。
B. 数据结构
如果 \(a\) 中各种字符出现的次数为如下柱形图：
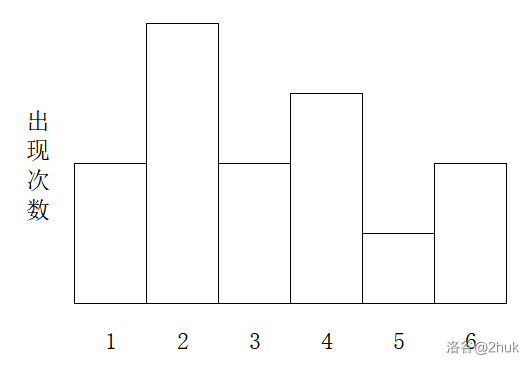
显然这样排列最优：
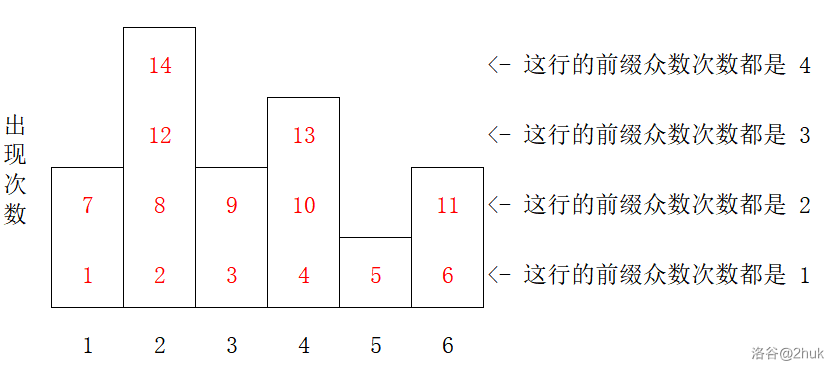
红字是这个数字重排后的下标。
考虑表示答案。显然一个数字 \(i\) 如果出现 \(cnt_i\)，那么他对答案的贡献是 \(1 +2+\dots+cnt_i\)。等差数列求和即可。即总答案为 \(\sum \dfrac{cnt_i(cnt_i+1)}2\)。
于是我们得到了一个不带修的解法。注意到每次单点修改后，\(cnt\) 数组中至多会有两个值发生改变。重新计算一下这两个值对答案的贡献即可。
复杂度线性。
C. Another Subsequence Problem
cdq 分治。
快进到如何计算 \(l \le mid,r \ge mid + 1\) 的 \([l, r]\) 的答案。
如果这个区间的右端点向右延伸了 \(k_0\) 的长度，即 \(r = mid + k_0\)，其中 \(k_0 < k\)，那么其左端点最多只能向左延伸 \(k-k_0\)，即左端点 \(l \ge mid-(k-k_0)+1\)。
随着 \(r\) 的增大，合法的 \(l\) 的数量只会减少 \(1\)。因此我们枚举 \(r\)（或者 \(k_0\)），动态维护目前仍合法的 \(l\) 的后缀积的和。然后做完了。
D. 互质子段
考虑若已经确定了 \(a\) 那么它的权值怎么算。
每次我们找到一个最短的前缀使得其 \(\gcd = 1\)。然后删掉这个前缀，重复操作。这个删前缀的次数就是答案。
考虑 DP。设 \(f(i, j)\) 表示考虑前 \(i\) 个数，且它所在的段的 \(\gcd = j\) 的方案数。
枚举 \(i + 1\) 位填什么。根据刚才所说，如果 \(i\) 这一段的 \(\gcd = 1\) 那么这一段必须结束，也就是说要从 \(i + 1\) 开始新的一段。即：
若不是则 \(i + 1\) 与 \(i\) 所在的段相同。即：
直接是 \(\mathcal O(nk^2)\) 的。能拿 \(40\)。
不会了。
E. 调色盘
我们为每种颜色指定一个“代表位置”。设颜色 \(i\) 的代表位置为 \(a_i\)，这里需要满足 \(c_{a_i} = i\)。
然后我们给每个点设一个权值 \(w\)。若 \(i\) 是颜色 \(c_i\) 的代表位置（即 \(a_{c_i} = i\)），那么将 \(i\) 的权值设置为颜色 \(j\) 在整棵树上的出现次数（即 \(w_i = cnt_{c_i}\)）。否则 \(w_i = 1\)。
那么如果不删除子树则答案为 \(\prod w_i\)。
考虑如果处理删除子树的操作。
我们的目的是，对于某个在 \(i\) 子树中出现过的颜色 \(j\)，我们都将它的代表位置的权值设为 \(1\)。此时 \(\prod w_i\) 就是答案。
注意到此时 \(i\) 子树内的所有点的权值都是 \(1\) 了，所以全局乘积可以通过 dfs 序转化成一个前缀和一个后缀的乘积。
此时最难做的地方是，我们不能直接将某个颜色的代表位置设为 \(1\)，因为后续处理其它点时，这个代表位置还需要用到。
因此我们考虑改变代表位置而不是删除代表位置。具体的，计算 \(i\) 的答案时，首先处理其所有儿子的子树。然后将 \(i\) 的代表位置更新为 \(i\)（将原代表位置的权值设为 \(1\)，将 \(i\) 的权值设为 \(cnt_{c_i}\)）。这是因为 \(i\) 是在 \(i\) 的子树内的，而刚才说的一段前缀乘一段后缀是不会计算上这颗子树内的。
而单点修改，区间（前缀和后缀）查询可以用线段树。总复杂度 \(\mathcal O(n \log n)\)。常数极大，需要很多卡常技巧。
