10.4 模拟赛（2025 炼石计划 NOIP 模拟赛 #7）
2025--炼石计划-- 9 月 25 日 --NOIP 模拟赛 #7【订正】 - 比赛 - 梦熊联盟 (mna.wang)
复盘
赢麻了。
浏览题。T1 没理解“中间节点”是啥意思，样例太大先不模拟了。
T2 什么东西，密铺？
T3 好像看懂了题。脑子中瞬间有一个 \(n^3\) DP，发现 \(n \le 200\) 感觉切了。但其实 DP 假的很离谱。
T4 又是数据结构。只会暴力。
顺着做吧。花了 1e4514min 模拟出了 T1 样例。感觉中间节点好像最多只有 \(1\) 个。尝试证明它，但是没证出来。
于是按照这个思路写了个 \(\mathcal O(n^3)\) 暴力。小样例当然过了，但大样例 \(n = 8000\) 需要跑很久。
算了一下需要跑一个小时左右（最后也就跑了 \(30\) 分钟）。终于跑出来了，发现与答案不对。所以这个结论是假的。先放弃了。
看 T2。哦原来不是密铺，只是求方案数。感觉好像不是很难。
\(k \le 6\)？想起了 这场 T4 和 这场 T4。分类讨论还是搜索？
先分类讨论吧。\(k = 1 \to 6\) 依次想解法。很快会了 \(k \le 3\) 的。\(k=4\) 的模拟了一会也差不多。再大就不会了。
模拟的时候感觉有点 DP 的感觉。于是尝试写了一个 DP，但是转移不了。
发现其实不是 DP。我可以枚举横/竖切的次数（\(k^2\)），然后整张图会被分成 \(k^2\) 个块。而块内不是不需要考虑的，缩成一个点就行。然后爆搜。
对吗？好像没有问题。发现爆搜可以替换成打表，于是另开了一个 bl.cpp。写完后稍微调了一会发现两个小样例都过了。
结论猜对了吗？？？？？？？？？对拍启动。
好像没有问题。
还有 1 个小时，拼暴力。
最后 \(40+100+15+15\)。实际上 T1 有个链感觉差不多也能做出来，但没来及。
总结
好的：
- 切了 T2。
- 没有因为低级错误挂分。
不足：
- T1 有些特殊性质分没拿到。
知识点
- T1：树的直径。
- T2：组合。
题解
T1. 旅行
有个定理：从树上任意一点出发，到达的最远点一定是直径端点。
所以你可以求出任意一条直径 \(s - t\)。考虑 \(u, v\) 的答案。
首先你从 \(u\) 走到 \(s, t\) 中较远的点，从 \(v\) 也走到 \(s, t\) 中较远的点。
如果此时它们到达的点相同，那么这条路就找到了。
否则，如果它们想再相遇，必须要有一个点跨过直径。而因为直径最长，所以取 \(\min\) 对它无效。
所以无论它们是否到达同一个点，答案相同。
所以答案为：
考虑计算 \(n(n-1)\) 个 \(u, v\) 的总答案。令 \(w_i = \max(dis_{i, s}, dis_{i, t})\)，所求：
经典的两个 \(\sum\) 的题目。将 \(w\) 升序排序，然后 \(\sum_{i=1}^n w_i(n-i)\)。
T2. 地砖
枚举横着切 \(i\) 刀，竖着切 \(j\) 刀。这里的切不要求全切。
显然 \(i + j \le k\)。所以这个枚举是 \(k^2\) 的。
假设全切，那么整张图会被分成 \((i+1) \times (j+1)\) 个大格。我们知道大格内部是不会有刀的（如果有就会在外层枚举而形成两个较小的格），所以我们可以将一个格视作一个点。
也就是将原来 \(n \times m\) 的大图视作 \((i+1)\times (j+1)\) 的图。
注意到这张图并不是最终图。因为我们刚才默认了每一刀都切满，但实际可能不是。
所以需要对这张图在做一遍原问题。因为大小很小所以可以爆搜。
对吗？注意到如果将大格缩点后这样切：
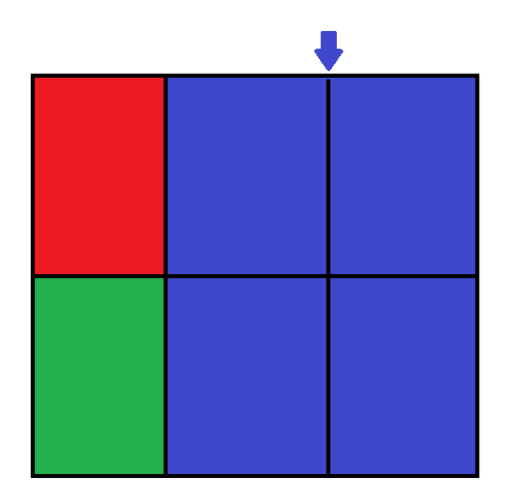
没有任何一个矩形的边界是被箭头指的那一列。所以这一列废了。在爆搜时要把这样的情况去掉。
注意到不需要真的写一个爆搜。可以打表。
