最小生成树 trick
经常做不出有关求最小生成树的题，而且最近网络赛上出得很多。
一般来说，给一张奇奇怪怪的图求其最小生成树，最简单的情况是模拟 kruskal。较复杂的（比如边数是 \(n^2\) 级别的）图可能会存在一些边用不到。
下面题目展示了一些图的形态，所求均为该图的最小生成树。
1. P5687 [CSP-S2019 江西] 网格图
一张 \(n \times m\) 的网格图，\((i, j)\) 与 \((i, j + 1)\) 有边权为 \(a_i\) 的边，\((i, j)\) 与 \((i + 1, j)\) 有边权为 \(b_j\) 的边。求最小生成树。
模拟 Kruskal。把输入的 \(a_{1\dots n},b_{1\dots m}\) 一块排序，然后按照权值从小到大依次处理一整行/列。
比如我们当前要处理第 \(i\) 行。显然这一行上有 \(m\) 个节点，\(m - 1\) 条边。如果我们能求出这些边中有 \(k\) 条我们要选择，那么把答案加上 \(k \times a_i\) 即可。
这里的选择是指两端点不连通的边的数量。
首先有一些情况是现在这 \(m\) 个点两两不连通，此时 \(k = m - 1\)。这些情况为：
- 这是第一次操作。
- 之前进行的操作都是列。
- 之前进行的操作都是行。
剩下的情况是之前既进行过行操作也进行过列操作。例如：
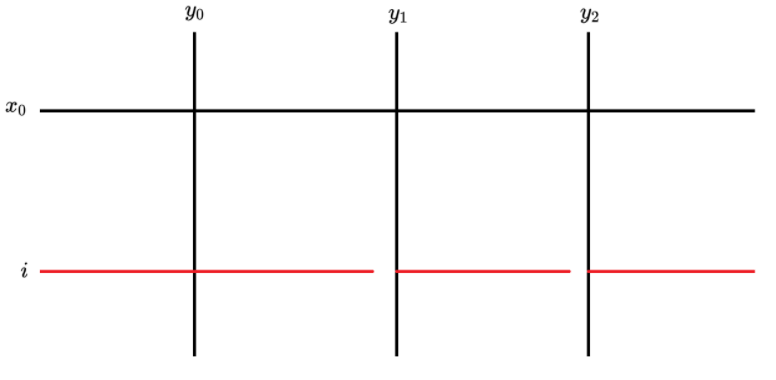
此时 \((i,y_1-1),(i,y_1)\) 连通，\((i,y_2-1),(i,y_2)\) 连通，我们应该减去这两条边。当然这样的前提是我们以前操作过 \(x_0\) 行。
令 \(c\) 表示之前操作列的此时，那么 \(k = m - c\)。
列同理不再赘述。
https://www.luogu.com.cn/record/175093830
2. [ABC364F] Range Connect MST
3. [ABC352E] Clique Connect
图中最初没有边。\(m\) 次操作，给定一个集合 \(S_i=\lbrace A_{i,1},A_{i,2},\dots,A_{i,K_i}\rbrace\)。对于每一对在 \(S_i\) 中且 \(u<v\) 的顶点 \(u,v\)。在 \(u\) 和 \(v\) 之间添加一条权重为 \(C_i\) 的边。求最小生成树。
边很多。
我们考虑 Kruskal 的做法，是将所有边按照边权排序，然后从小到大处理每条边。这意味着如果真的暴力建图并将边权排序的话，第 \(i\) 次操作加的边在新的数组中是连续的，但显然顺序不重要。而且我们知道加的 \(\dbinom {|S_i|}2\) 条边中最多只会用到 \(|S_i| - 1\) 条，如果多于这个数必定有环，又因为顺序不重要所以我们直接将相邻两个点连边即可。
优化边的数量后，跑朴素 Kruskal 即可。
4. [ABC355F] MST Query
图中最初没有边。\(q\) 次操作，给定 \(l_i, r_i\)，对于所有 \(j \in [l_i,r_i]\)，在点 \(n + i\) 和点 \(j\) 之间添加一条权重为 \(c_i\) 的边。求最小生成树。
仍然模拟 Kruskal。我们将所有操作离线，然后按照 \(c_i\) 排序。顺次处理每次操作。
操作 \(i\) 结束后 \([l_i, r_i]\) 中的点一定连通。我们标记 \(i\) 与 \(i + 1\) 的联通情况为 \(a_i\)，即若 \(a_i = 1\) 则 \(i, i+1\) 连通，反之亦然。
首先 \(n + i\) 号点一定会与 \(l_i\) 连边。因为在此之前 \(n + i\) 是孤立点，没有任何点与它连通。
我们考虑 \(n + i\) 是否会与 \(l_i+1\) 连边，即判断此时 \(l_i + 1\) 是否与 \(n + i\) 连通。此时因为唯一与 \(n + i\) 有边的点是 \(l_i\)，所以问题等价于 \(l_i+1\) 是否与 \(l_i\) 连通。不难发现这是 \(a_i\) 的定义。
同理继续处理 \(l_i+2\)。这个点是否与 \(n + 1\) 连边也取决于 \(a_{i+1}\)。
所以我们得到，若 \(n + i\) 与 \(j \in [l_i, r_i]\) 有连边，当且仅当：
- \(j = l_i\)；
- 或 \(a_{j-1}=0\)。
所以我们需要快速求出 \([l_i+1,r_i]\) 中 \(0\) 的数量。同时每次操作后，\([l_i,r_i]\) 中的点已经全部联通了，所以这次操作结束后，\([l_i, r_i-1]\) 应该被全部推平成 \(0\)。而维护区间推平和求 \(0\) 的数量可以用线段树。
https://www.luogu.com.cn/record/175172388
5. MX 模拟赛 数字生成树（\(60\) 部分分）
给定一张图，求最小按位或生成树。如其名称，所求的生成树需满足所有边权的按位或和最小。
这题跟 Kruskal 没关系。
按位或和最小，我们可以从高到低枚举每个二进制位，判断这个答案的这个二进制位能否为 \(0\)。
如果这一位是 \(0\)，根据按位或的定义，所有边权的第 \(i\) 位为 \(1\) 的边必须不选。我们在图上将这些边删掉。如果剩下的边仍能保证图的连通则答案的第 \(i\) 个二进制为 \(0\)。否则把刚才删的边加回来，此时答案的这一位不得不是 \(1\)。
