斜率优化

P5785 [SDOI2012] 任务安排

快进到 DP 式子：

\[f(i) = \min\{f(j) + T(i) \times (C(i) - C(j)) + m \times (C(n) - C(j))\} \]

把 \(\min\) 去掉，然后拆括号：

\[f(i) = f(j) + T(i) \times C(i) - T(i) \times C(j) + m \times C(n) - m \times C(j) \]

移项：

\[\underline{f(j)}_y = \underline{(T(i) + m)}_k \times \underline{C(j)}_x + \underline{f(i) - T(i) \times C(i) -m \times C(n)}_b \]

这是直线解析式 \(y = kx + b\) 的形式。

我们的目标是让 \(f(i)\) 最小。这是因为我们刚才将 \(\min\) 去掉了，让 \(f(i)\) 最小就是为了体现这个 \(\min\)。

因为我们正在枚举 \(i\)，所以与 \(i\) 有关的信息在这个式子中都是常数。不妨将上式写成：

\[\underline{f(j)}_y = k \times \underline{C(j)}_x + \underline{f(i) + c}_b \]

其中 \(k = T(i) + m\)，\(c = -T(i) \times C(i) - m \times C(n)\)。这两个值只与 \(i\) 有关，

---

我们希望最小化 \(f(i)\)，可以进一步退化为最小化 \(f(i) + c\)（即截距 \(b\)）。因为 \(c\) 是固定的。

想象有一条直线。它的截距 \(b\) 暂未确定，但是方向 \(k\) 确定了。我们希望让这条线经过某一个点 \((C(j), f(j))\)，且截距最小。

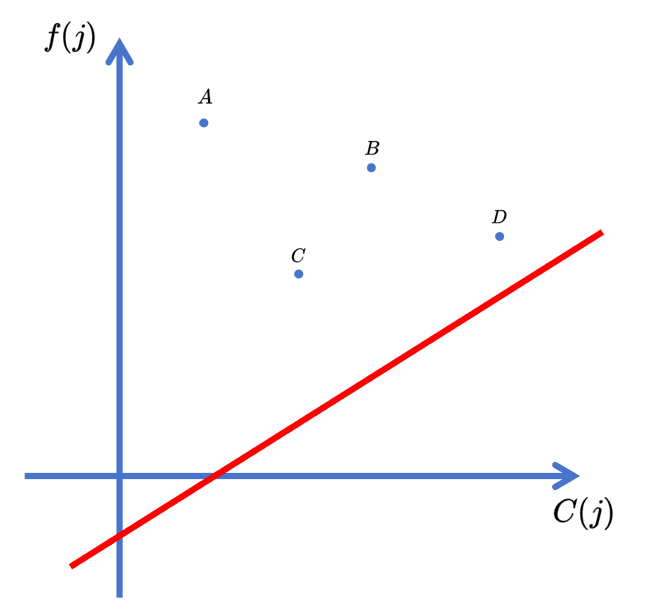
显然这张图中，点 \(D\) 是最好的选择。因为：

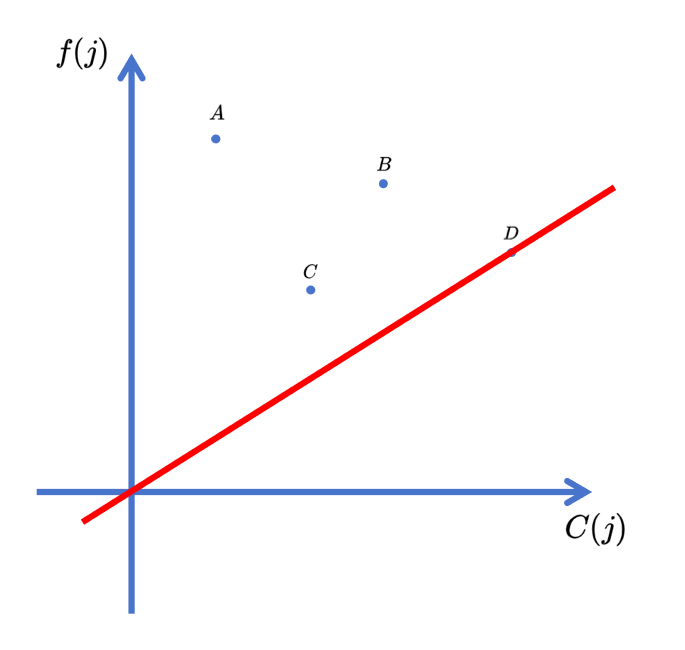
此时 \(b = 0\)（啊？随手画的图这么巧？），最小。

但是不一定对于任意的 \(k\) 都是 \(D\) 最好。当 \(k\) 更大或 \(k\) 更小时：

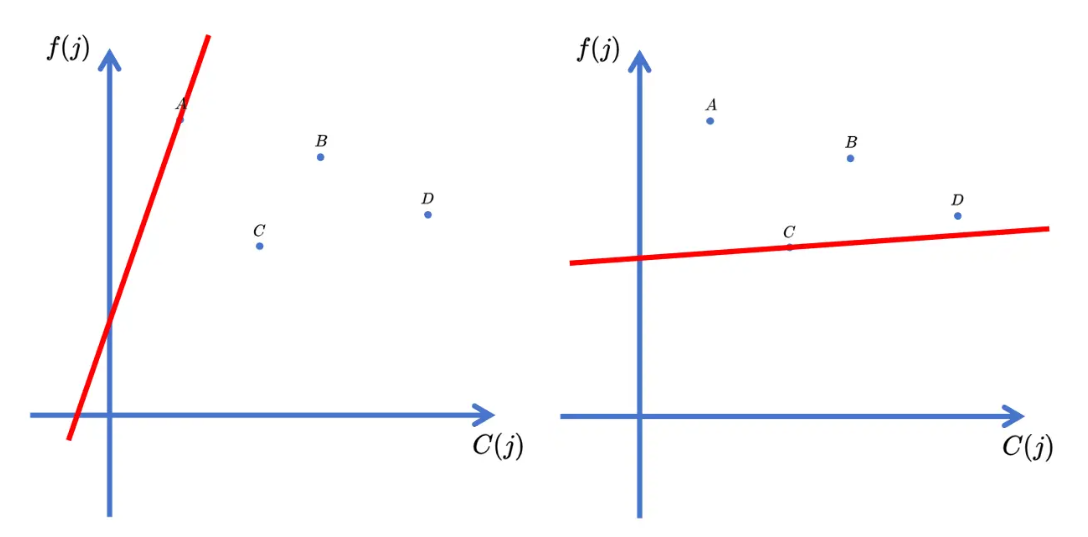
但是不难发现 \(k\) 取何值时，点 \(B\) 都不可能被取到。这提示我们可以只维护 \((C(j), f(j))\) 这些点的下凸壳。

---

我们考虑动态维护这个凸壳上的点。

我们每次判断最后加入的两个点 \(A, B\)（\(B\) 为最后一个，\(A\) 为倒数第二个），以及即将加入的点 \(C\)。那么将这个新点加入后，如果 \(B\) 将要从凸壳中删除，就意味着 \(BC\) 的斜率小于 \(AC\) 的斜率。

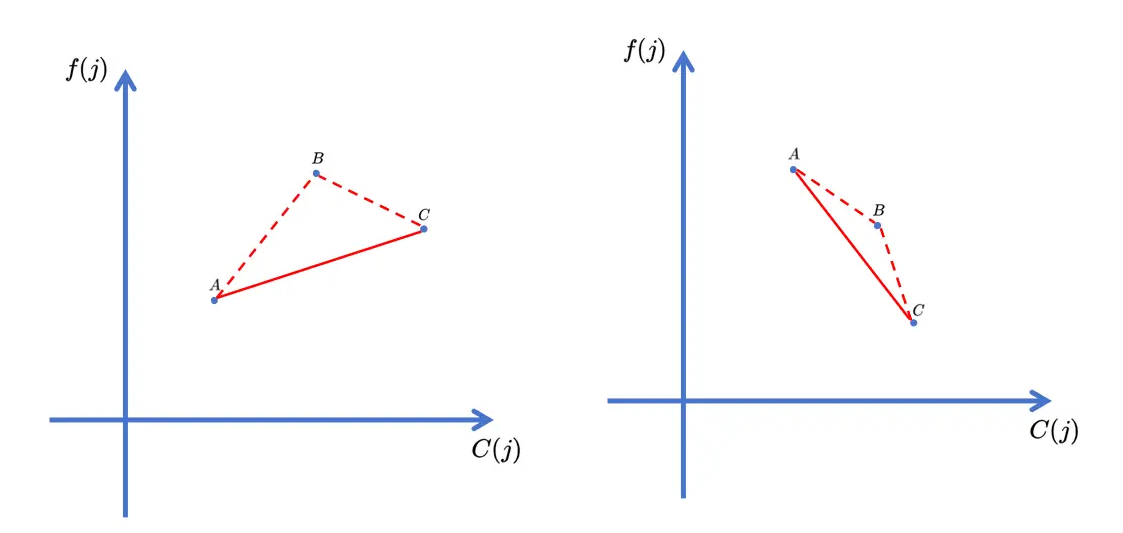
若将 \(B\) 删除后，接下来的两个点仍满足上述条件，可以继续循环删除。

---

那么我们已经用队列维护当前凸壳中的点了。那么那个点是转移 \(f(i)\) 时用的呢？

换言之，我们需要找到这个凸壳上的所有点中，被斜率为 \(k\) 的直线从下往上扫描的过程中，第一个接触的点。例如：

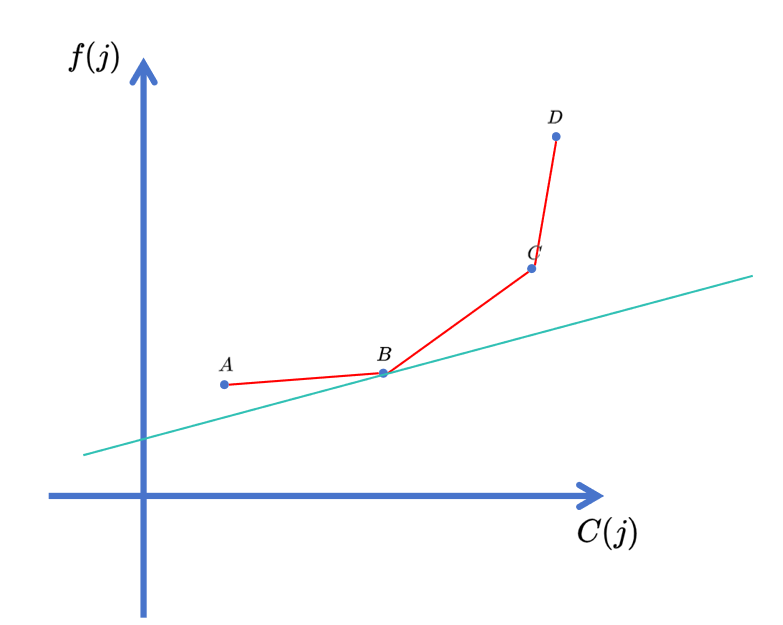
其中绿色线斜率为 \(k\)。

不难发现若答案为 \(B\)，那么一定有 \(AB\) 的斜率比 \(k\) 小，\(BC\) 斜率比 \(k\) 大。而这个下凸包相邻两点的斜率是单调递增的，所以我们可以二分找到这个决策点。