字符串做题笔记
\(\color{#3498D8}(1)\) P3065 [USACO12DEC] First! G
- 给定 \(n\) 个互不相同的字符串 \(s_i\)。求哪些 \(i\) 满足存在一种安排二十六个小写字母大小顺序的方式,使得 \(s_i\) 字典序最小。
- \(n \le 3 \times 10^4\)。
首先将所有字符串按到 Trie 树上。例如样例:
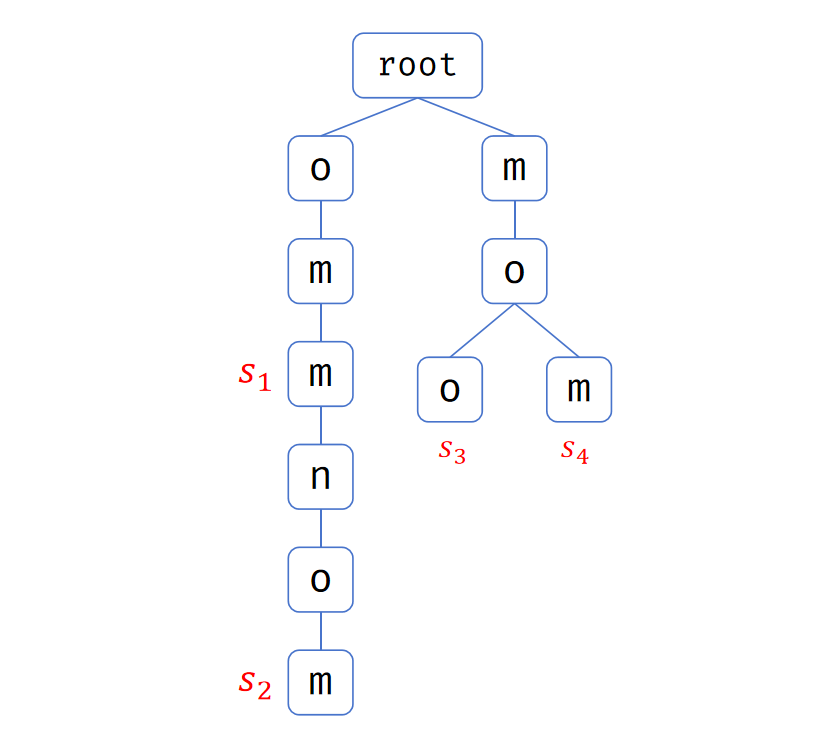
如果我们想让 \(s_3\) 最小,那么在第一层需要保证 \(\texttt{m} < \texttt{o}\) 以保证 \(s_3 < s_1\) 且 \(s_3 < s_2\)。在第三层又需要保证 \(\texttt{o} < \texttt{m}\) 以保证 \(s_3 < s_4\)。显然 \(\texttt{m} < \texttt{o}\) 和 \(\texttt{o} < \texttt{m}\) 是不可能同时成立的。所以 \(s_3\) 是不合法的。
其次,因为 \(s_1\) 是 \(s_2\) 的真前缀,所以一定有 \(s_1 < s_2\)。因此 \(s_2\) 也不合法。
一般化的,我们枚举 \(i\) 表示判断 \(s_i\) 是否有可能成为答案。首先如果某个字符串是 \(s_i\) 的真前缀,那么 \(s_i\) 不是答案;否则,在 Trie 树上 dfs。将当前节点与兄弟节点表示的字母连有向边。最后判断是否有环即可。
\(\color{#3498D8}(2)\) P4551 最长异或路径
- 给定一棵 \(n\) 个点的带权树,结点下标 \(1 \sim n\)。寻找树中找两个结点,求最长的异或路径。异或路径指的是指两个结点之间唯一路径上的所有边权的异或。
- \(n \le 10^5\),\(0 \le w < 2^{31}\)。
首先令 \(f(i)\) 表示 \(i\) 到根的异或路径,那么 \(i, j\) 的异或路径 \(= f(i) \operatorname{xor} f(j) \operatorname{xor} f(\operatorname{lca}(i, j)) \operatorname{xor} f(\operatorname{lca}(i, j)) = f(i) \operatorname{xor} f(j)\)。也就是希望最大化 \(f(i) \operatorname{xor} f(j)\)。
最经典的贪心 + Trie 树做法。枚举 \(i\),从高到低逐二进制位 \(k\),如果存在一个 \(j\) 使得 \(f(i), f(j)\) 的第 \(k\) 位不同,那么一定选择这个 \(j\),因为这会收获 \(2^k\) 的价值。如果不存在这样的 \(j\),没办法只能放弃这一位。然后继续贪心下一位。
\(\color{#3498D8}(3)\) CF727E Games on a CD
- 已知 \(m\) 个长度为 \(k\) 互不相同的字符串 \(r_1 \dots, r_m\) 和一个长度为 \(nk\) 的环形字符串 \(s\),问是否能从 \(r_1\dots r_m\) 中选出 \(n\) 个组成字符串 \(s\),并给出方案。
- \(n, k, m \le 10^5\),\(nk \le 10^6\)。
如果不是环形字符串,做法显然。将 \(s\) 连续的划分成 \(n\) 个长度为 \(k\) 的子串 \(t_1, t_2, \dots, t_n\),那么此时就需要判断是否可重集 \(\{t_1, t_2, \dots, t_n\} \subseteq \{r_1, r_2, \dots, r_m\}\)。字符串 Hash 即可。
因为是环形字符串,所以第一步是倍长然后循环移位。不难发现移位最多移 \(k\) 次,因为移 \(i\) 和 \(i \bmod k\) 次是等价的。
\(\color{#9D3DCF}(4)\) CF985F Isomorphic Strings
- 给你一个长度为 \(n\) 的字符串,\(m\) 次询问,问两个相同长度的子串是否匹配。我们称两个子串是匹配的,当且仅当其满足其中一个子串的字母可替代另一个子串的字母。
- \(n, m \le 2 \times 10^5\)。
我们可以分别统计对于每种字符 \(\texttt a \sim \texttt z\) 在 \([l_1, r_1], [l_2, r_2]\) 出现的位置构成的集合。如果存在一种将这 \(26\) 个集合一一对应的方式,就代表两个子串时匹配的。
实现上,我们维护 \(26\) 个字母在每个位置是否出现的 \(01\) 状态。然后做 \(01\) 状态的字符串 Hash。对于判断区间 \([l_1, r_1], [l_2, r_2]\) 是否匹配而言,我们只需要将 \(26\) 个字母的区间 Hash 值排序,并判断是否完全相同即可。
\(\color{#3498D8}(5)\) [IOI2008] Type Printer
你需要利用一台可移动的打印机打印出 \(n\) 个单词。这种可移动式打印机是一种老式打印机,它需要你将一些小的金属块(每个包含一个字母)放到打印机上以组成单词。然后将这些小金属块压在一张纸上以打印出这个词。这种打印机允许你进行下列操作:
- 在打印机当前词的末端(尾部)添加一个字母;
- 在打印机当前词的尾部删去一个字母(将打印机当前词的最后一个字母删去)。仅当打印机当前至少有一个字母时才允许进行该操作;
- 将打印机上的当前词打印出来。
初始时打印机为空,或者说它不含任何带字母的金属块。打印结束时,允许有部分字母留在打印机内。同时也允许你按照任意的次序打印单词。
由于每一个操作都需要一定时间,所以需要你尽可能减少所需操作的总数目(将操作的总数最小化)。
你需要编写一个程序,给定所要打印的 \(n\) 个单词,找出以任意次序打印所有单词所需操作的最小数目,并输出一种这样的操作序列。
\(n \le 25000\),\(|S| \le 20\)。
对字符串建 Trie 树。接下来是一个经典的树上问题。
显然对于字符串 \(\texttt{aba}, \texttt{abbc}\) 建出的 \(\texttt a \to \texttt b^{\nearrow ^{\huge \texttt a}}_{\searrow _{\huge \texttt b \to \texttt c}}\) 而言,我们一定先遍历上面的分支。走到下面的 \(\texttt c\) 后就可以停止整个过程了。因为 \(c\) 是深度最深的节点。
因为答案为 \(2(n - 1) - \max dep_i + n\)。剩下的就是模拟了。
\(\color{#6D3DCF}(6)\) CF961F k-substrings
- 给定一个长度为 \(n\) 的字符串 \(T\) 。定义 \(k\) 子串表示 \(S_k , S_{k+1} \cdots S_{n - k +1}\)。求每个 \(k\) 子串 \(k=1,2,3...\lceil \frac n 2 \rceil\) 的 border 长度。这里要求 border 的长度为奇数。
- \(n \le 10^6\)。
考虑:
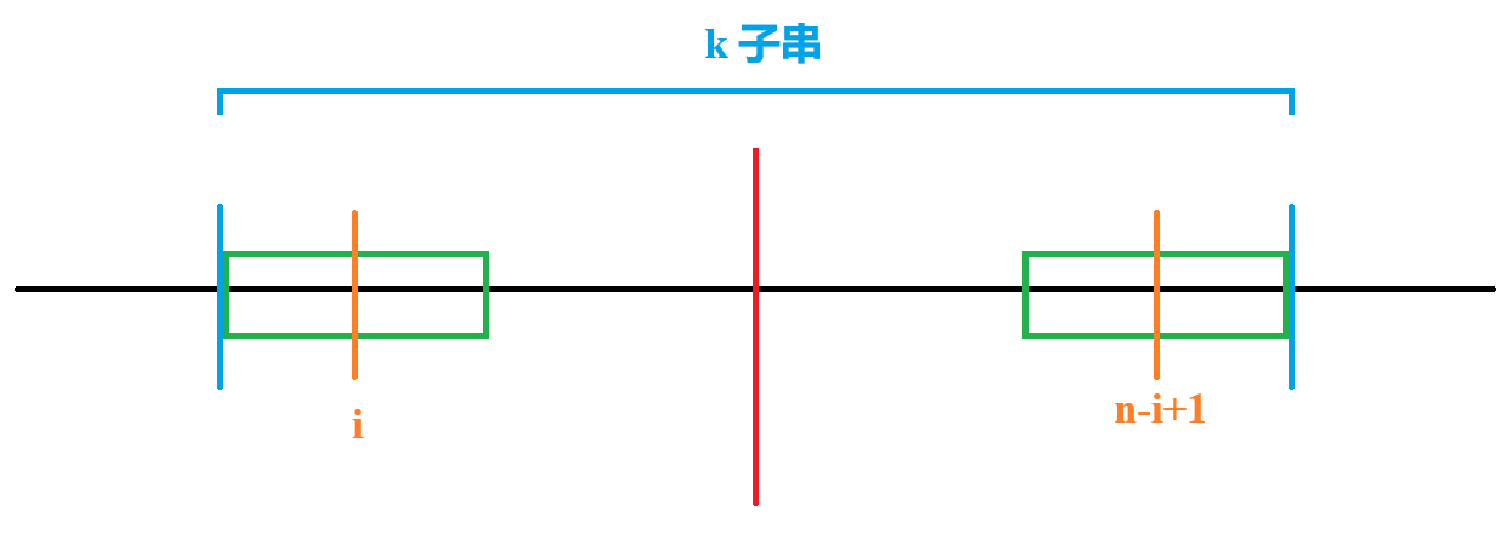
其中蓝色部分为 \(k\) 子串,绿色的是这个 \(k\) 子串 border,红线是原串中线,橙线分别是这两个 border 的中线。因为题目要求 border 长度为奇数,所以橙线坐标一定为整数。
第一条橙线的下标为 \(i\),那么根据 \(k\) 子串在下标上的对称性,另一条橙线的下标为 \(n - i + 1\)。我们考虑枚举第一条橙线的下标 \(i = 1, 2, \dots, \lfloor \frac n2 \rfloor\)。
接下来显然可以二分最大的 border 的半径 \(r\),并计算这个 border 可能会对哪些 \(k\) 子串的答案构成影响。
具体地,二分出最大的 \(r\) 使得 \(s[i-r+1, i+r-1] = s[n-i-r+2, n-i+r]\),这一步可以用字符串 Hash 判断。
然后考虑对于 \((i-r+1)\) 子串,此时可以用 \(2r - 1\) 更新它的答案,表示当前这个子串的长度。同理,对于 \((i-r+2)\) 子串,此时我们可以用 \(2r-3\) 更新它的答案,因为这个子串不能包含 \(i - r + 1\) 这个位置,因此长度减了 \(2\)。以此类推,贡献的形式呈一个公差为 \(-2\) 的等差数列。
于是问题就转化成了:
- 若干次操作,将连续若干数与一个公差为 \(-2\) 的等差数列取 \(\max\)。
做法见 线段树做题笔记 (7)。
\(\color{#3D4DCF}(7)\) CF126B Password
- 给定一个字符串 \(S\),输出既是 \(S\) 的前缀又是 \(S\) 的后缀同时又在 \(S\) 中间出现过的最长子串。或报告无解。
- \(|S| \le 10^6\)。
显然我们只需要确定两个值 \(l, r\),表示这个子串长度为 \(l\),第一次在中间出现的结束位置为 \(r\),我们就可以确定这三个子串 \([1, l], [r-l+1,r], [n-l+1, n]\)。
KMP 求出每个前缀的 botder 长度 \(f(i)\)。那么 \(f(n), f(f(n)), f(f(f(n))) \dots\) 都是 \(S\) 的公共前后缀。按照这个顺序枚举(即最开始 \(l = f(n)\),每次 \(l \gets f(l)\))判断当前 \(l\) 是否合法,即是否存在一个满足条件的 \(r\)。
怎么做到 \(\mathcal O(1)\) 判断呢?也就是判断是否存在一个 \(r\),满足 \([1, l] = [r-l+1, r]\)。显然我们只需要将 \(f(2), f(3), \dots, f(n - 1)\) 都标记上,然后判断 \(l\) 是否被标记即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号