图论做题笔记
\(\color{#52A41A}(1)\) CF173B Chamber of Secrets
给定一张 \(n\times m\) 的包含
#和.的图,现有一束激光从左上角往右边射出。每次遇到
#,你可以选择光线改变为上下左右四个方向之一,也可以不改变。求至少需要改变几次方向,可以使激光从第 \(n\) 行向右射出。
\(n, m \le 10^3\)。
显然总共有 \(4nm\) 种状态,即在每个位置有 \(4\) 种当前面对的方向。
发现转移是类似于图上的边,且边权仅有 \(0\) 和 \(1\)。所以 01bfs 即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
const int N = 1010, M = 10000100;
int n, m;
char g[N][N];
struct Node {
int a, b, dx, dy;
bool operator <(const Node &h) const {
if (a == h.a) {
if (b == h.b) {
if (dx == h.dx) return dy < h.dy;
return dx < h.dx;
}
return b < h.b;
}
return a < h.a;
}
};
std::deque<Node> q;
int dis[N][N][3][3];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; ++ i ) scanf("%s", g[i] + 1);
memset(dis, 0x3f, sizeof dis);
q.push_back({1, 1, 0, 1});
dis[1][1][1][2] = 0;
const std::vector<int> tx({1, 0, -1, 0}), ty({0, -1, 0, 1});
while (!q.empty()) {
int x = q.front().a, y = q.front().b, dx = q.front().dx, dy = q.front().dy;
q.pop_front();
if (g[x][y] == '#') {
for (int i = 0; i < 4; ++ i ) {
if (dis[x][y][tx[i] + 1][ty[i] + 1] > 1e9) {
dis[x][y][tx[i] + 1][ty[i] + 1] = dis[x][y][dx + 1][dy + 1] + 1;
q.push_back({x, y, tx[i], ty[i]});
}
}
}
if (x + dx >= 1 && x + dx <= n && y + dy >= 1 && y + dy <= m && dis[x + dx][y + dy][dx + 1][dy + 1] > 1e9) {
dis[x + dx][y + dy][dx + 1][dy + 1] = dis[x][y][dx + 1][dy + 1];
q.push_front({x + dx, y + dy, dx, dy});
}
}
printf("%d\n", dis[n][m][1][2] < 1e9 ? dis[n][m][1][2] : -1);
return 0;
}
\(\color{#FFC116}(2)\) CF1063B Labyrinth
给定一张 \(n\times m\) 的包含
*和.的图,*是不能经过的障碍。给定你的起点 \((r,c)\),每次你可以往上下左右四个方向之一移动一步。
限制了你的向左移动的次数不超过 \(x\) 和向右移动的次数不超过 \(y\),求你能到达多少个格子。
\(n, m \le 2 \times 10^3\)。
枚举终点。可以发现如果确定了往右走的步数和最终到达的与起点的列数的差,就可以轻易的求出需要往左走的步数。
所以我们可以预处理出从起点到达每个点所需要的最小的往左次数,然后枚举终点判断合法即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
const int N = 2024;
int n, m, sx, sy, x, y;
char g[N][N];
int f[N][N]; // 到达 (i, j) 的最小向左次数
const std::vector<int> dx({0, 1, 0, -1}), dy({1, 0, -1, 0});
signed main() {
scanf("%d%d%d%d%d%d", &n, &m, &sx, &sy, &x, &y);
for (int i = 1; i <= n; ++ i ) scanf("%s", g[i] + 1);
memset(f, 0x3f, sizeof f);
std::list<std::pair<int, int> > q;
q.push_back({sx, sy});
f[sx][sy] = 0;
while (q.size()) {
int x = q.front().first, y = q.front().second;
q.pop_front();
for (int i = 0; i < 4; ++ i ) {
int a = x + dx[i], b = y + dy[i];
if (a >= 1 && a <= n && b >= 1 && b <= m && g[a][b] == '.' && f[a][b] > f[x][y] + (i == 2)) {
f[a][b] = f[x][y] + (i == 2);
if (i == 2) q.push_back({a, b});
else q.push_front({a, b});
}
}
}
int res = 0;
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= m; ++ j )
if (g[i][j] == '.' && f[i][j] < 1e9)
res += f[i][j] <= x && j - (sy - f[i][j]) <= y;
printf("%d\n", res);
return 0;
}
\(\color{#BFBFBF}(3)\) BZOJ5450 轰炸
- 有 \(n\) 座城市,城市之间建立了 \(m\) 条有向的地下通道。你需要发起若干轮轰炸,每轮可以轰炸任意多个城市。但每次轰炸的城市中,不能存在两个不同的城市 \(i,j\) 满足可以通过地道从城市 \(i\) 到达城市 \(j\)。你需要求出最少需要多少轮可以对每座城市都进行至少一次轰炸。
- \(n, m \le 10^6\)。
首先将 scc 缩点。因为在一次轰炸中,不可能同时选择在相同 scc 中的点。因为这两个点可以互相到达。
接下来原图变成了一个 DAG。那么显然也不能轰炸选择在同一条链上的点。因为这样其中一个会到达另一个。
所以最直观的想法即,答案为 DAG 上的最长路,其中每个点的点权表示原 scc 中的点的数量。考虑证明这件事情(设答案为 \(ans\),最长路径为 \(L\),最长路径的点权和为 \(d\)):
- \(ans \ge d\)。因为不能同时轰炸 \(L\) 上的两个点,所以在一次操作中,最多轰炸 \(L\) 上的一个点。因为这些点总共有 \(d\) 个,所以操作总次数一定不少于 \(d\) 次。
- 存在 \(ans = d\) 的方案。因为 \(L\) 是最长路,所以其它的路径长度一定小于等于 \(d\)。所以我们可以在轰炸 \(L\) 上的一个点的同时,轰炸其它每个链上的一个点。显然轰炸的点是合法的。因为其它路径长度都 \(\le d\),所以当轰炸完 \(L\) 时,其它链也已经轰炸完了。
所以直接复制 P3387 【模板】缩点 即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 1000000 + 10, M = N * 2;
int n, m, w[N], a, b;
int h[N], e[M], ne[M], idx;
pair<int, int> edges[M];
int dfn[N], low[N], ts, stk[N], ttt;
bool st[N];
int id[N], sum[N], cnt;
int d[N];
int q[N], hh, tt = -1;
int f[N];
void add(int a, int b, bool flg = false) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
if (flg) ++ d[b];
}
void Tarjan(int u) {
dfn[u] = low[u] = ++ ts;
stk[ ++ ttt] = u, st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!dfn[j]) {
Tarjan(j);
low[u] = min(low[u], low[j]);
}
else if (st[j])
low[u] = min(low[u], dfn[j]);
}
if (dfn[u] == low[u]) {
int y;
do {
y = stk[ttt -- ];
st[y] = false;
sum[cnt] += w[y];
id[y] = cnt;
} while (y != u);
++ cnt;
}
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 1; i <= n; ++ i ) w[i] = 1;
for (int i = 1; i <= m; ++ i ) {
cin >> a >> b;
add(a, b);
edges[i] = {a, b};
}
for (int i = 1; i <= n; ++ i )
if (!dfn[i])
Tarjan(i);
memset(h, -1, sizeof h);
idx = 0;
for (int i = 1; i <= m; ++ i ) {
int a = id[edges[i].first], b = id[edges[i].second];
if (a != b) add(a, b, true);
}
memset(f, -0x3f, sizeof f);
for (int i = 0; i < cnt; ++ i )
if (!d[i])
q[ ++ tt] = i,
f[i] = sum[i];
while (hh <= tt) {
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i]) {
int j = e[i];
if (!( -- d[j])) q[ ++ tt] = j;
}
}
for (int i = 0; i < cnt; ++ i ) {
int k = q[i];
for (int j = h[k]; ~j; j = ne[j]) {
int v = e[j];
f[v] = max(f[v], f[k] + sum[v]);
}
}
cout << *max_element(f, f + cnt);
return 0;
}
\(\color{#52A41A}(4)\) CF721C Journey
- 给定一张 \(n\) 个点 \(m\) 条边的有向无环图,边有边权。构造一条 \(1 \to n\) 的路径使得其边权和 \(\le k\) 且经过的点数最多。
- \(n, m \le 5 \times 10^3\),\(k \le 10^9\)。
最简单的想法是设状态 \(f_{i, j}\) 表示 \(1 \to i\) 的边权和 \(\le j\) 的路径的最多点数。那么答案为 \(f_{n, k}\)。
显然状态数会爆炸。参照 AT_dp_e 的思路,我们将状态和值交换,即重新令 \(f_{i, j}\) 表示 \(1 \to i\) 的路径上经过了 \(j\) 个点的最小边权和。剩下的就是平凡的转移了。
一些细节:
- 对于那些没法从 \(1\) 到达的点,我们是不需要考虑它们的。因此我们将剩下的点建一张新图,那么这张图中拓扑排序的起点只有一个——\(1\) 点。
- 对于输出方案,按照一般的套路,维护每个 DP 状态是由哪里转移而来即可。
$\color{blue}\text{Code}$
int n, m, k;
int f[N][N]; // f[i][j] : 从 1 --> i 不超过经过 j 个点的最短路径
int pre[N][N];
bool st[N];
struct Gragh {
int d[N];
vector<pair<int, int> > g[N];
void add(int a, int b, int c) {
g[a].emplace_back(b, c);
++ d[b];
}
vector<pair<int, int> > operator [](int u) {
return g[u];
}
}G1, G2;
void dfs(int u) {
if (st[u]) return;
st[u] = true;
for (auto v : G1[u]) dfs(v.first);
}
void Luogu_UID_748509() {
fin >> n >> m >> k;
while (m -- ) {
int a, b, c;
fin >> a >> b >> c;
G1.add(a, b, c);
}
dfs(1);
for (int u = 1; u <= n; ++ u )
if (st[u])
for (auto t : G1[u]) {
int v = t.first, w = t.second;
if (st[v]) G2.add(u, v, w);
}
queue<int> q;
q.push(1);
memset(f, 0x3f, sizeof f);
f[1][1] = 0;
int cnt = 0;
while (q.size()) {
int u = q.front();
q.pop();
for (auto t : G2[u]) {
int v = t.first, w = t.second;
for (int i = 1; i <= n; ++ i ) {
ll x = f[u][i - 1] + w;
if (x > k) continue;
if (x < f[v][i]) {
f[v][i] = f[u][i - 1] + w;
pre[v][i] = u;
}
}
if (!( -- G2.d[v])) q.push(v);
}
}
for (int i = n; i; -- i )
if (f[n][i] <= k) {
cout << i << '\n';
int x = n, y = i;
stack<int> res;
while (y) {
res.push(x);
x = pre[x][y -- ];
}
while (res.size()) fout << res.top() << ' ', res.pop(); puts("");
return;
}
}
\(\color{#52A41A} (5)\) CF731C Socks
- 你有 \(n\) 只袜子,共有 \(k\) 种颜色,有 \(m\) 天。每只袜子有它的初始颜色。在第 \(i\) 天,你会穿第 \(l_i\) 只和第 \(r_i\) 只袜子。求最少改变多少袜子的颜色,使得你每天穿的两只袜子颜色相同。
- \(n, k, m \le 2 \times 10^5\)。
将 \(l_i, r_i\) 连边,会形成若干个连通块。显然每个连通块内的袜子颜色应该是相同的。
对于每个连通块独立考虑。我们希望将这个连通块内的颜色统一,且操作次数最少,最直观的想法就是全部染成出现次数最多的颜色。
令连通块大小为 \(s\),最多的颜色出现了 \(t\) 次,那么答案即 \(\sum (s - t)\)。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m, k, c[N];
int p[N];
int fifa(int a) {
return a == p[a] ? a : p[a] = fifa(p[a]);
}
map<int, int> mp[N];
int mx[N], cnt[N], res;
int main() {
cin >> n >> m >> k;
for (int i = 1; i <= n; ++ i ) cin >> c[i], p[i] = i;
for (int i = 1, u, v; i <= m; ++ i ) {
cin >> u >> v;
p[fifa(u)] = fifa(v);
}
set<int> S;
for (int i = 1; i <= n; ++ i ) {
int f = fifa(i);
S.insert(f);
mx[f] = max(mx[f], ++ mp[f][c[i]]);
++ cnt[f];
}
for (int i : S) res += cnt[i] - mx[i];
cout << res;
return 0;
}
\(\color{#52A41A}(6)\) CF412D Giving Awards
- 请你构造 \(1 \sim n\) 排列 \(P\),满足给定的 \(m\) 条形如 \((u, v)\) 的限制,表示不存在 \(P_i = u\) 且 \(P_{i + 1} = v\)。保证不存在两个限制 \(\mathbf{(u, v)}\) 和 \(\mathbf{(v, u)}\)。
- \(n \le 3 \times 10^4\),\(m \le 10^5\)。
连 \(u \to v\) 的有向边,然后 dfs 整张图。在 \(u\) 的出边全部访问结束后,将 \(u\) 加入答案队列的队尾。
考虑证明这种构造一定是正确的。可以画出一颗 dfs 树,分析三种边的合法性:
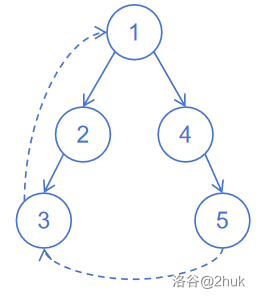
- 树边,例如 \(4 \to 5\)。根据我们的做法,\(4\) 一定在 \(5\) 之后访问。这样是合法的。
- 返祖边,例如 \(3 \to 1\)。由于题目保证「不存在两个限制 \((u, v)\) 和 \((v, u)\)」,所以这条返祖边一定不是指向它的父亲,而是跨越至少一个点。这意味着尽管有 \(3 \to 1\) 这条边,但由于 \(1\) 是祖先,所以它已经在前面被访问过,再次访问到 \(3\) 时它们之间已经隔着若干个点了(例如图中的 \(2\))。所以这样是合法的。
- 横叉边,例如 \(5 \to 3\)。同样的思路,在树上 \(3, 5\) 一定不是直接相连的,而是隔着几个点。这样也是合法的。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10;
int n, m;
vector<int> g[N];
bool st[N];
void dfs(int u) {
if (st[u]) return;
st[u] = true;
for (int v : g[u]) dfs(v);
cout << u << ' ';
}
int main() {
cin >> n >> m;
while (m -- ) {
int a, b;
cin >> a >> b;
g[a].push_back(b);
}
for (int i = 1; i <= n; ++ i ) dfs(i);
return 0;
}
\(\color{#3498D8} (7)\) CF118E Bertown roads
- 给定一张 \(n\) 个节点 \(m\) 条边的无向联通图。构造一种为每条边都确定一个方向的方案,使得这张图成为一个 scc。或报告无解。
- \(n \le 10^5\),\(m \le 3 \times 10^5\)。
若原图不是一个 dcc,即存在桥,那么一定无解。这是显然的。
否则,我们建一颗 dfs 树,并将树边的方向定为 父亲 \(\to\) 儿子,将返祖边的方向定为 后代 \(\to\) 祖先。显然不存在横叉边。
考虑证明这样做是可行的:
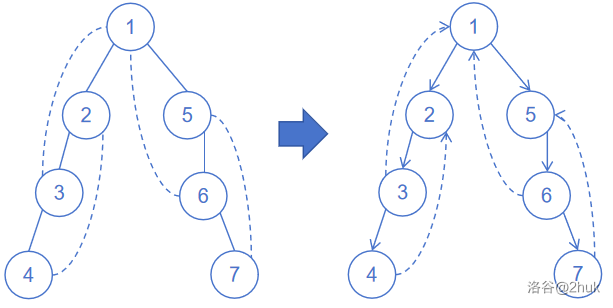
- 由于树边都是向下指,所以祖宗可以到达它的所有后代,包括但不限于祖先可以到达所有节点。
- 对于叶子节点,由于图中不存在桥,所以它一定存在一条返祖边。而这条边指向的祖宗要么为根,要么也存在一条返祖边。以此类推。所以叶子节点总能到达根。然后到达所有节点。
- 对于一般的节点,它可以通过树边到达叶子,再到达根,再到达所有节点。
实现上,我们从 1 开始 dfs。当走到一个已经做过的点时,证明这条边是返祖边,它的真正方向应该是深度深的指向深度浅的。否则若这个点是第一次访问,证明这条边是树边,它的真正方向应该是深度浅的指向深度深的。
所以需要 dfs 预处理出每条树边和返祖边,以及每个点的深度。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 600010;
struct Edge {
int a, b, id;
}edges[N];
int n, m;
vector<pair<int, int> > g[N], tr[N];
bool vis[N], st[N], vise[N];
int w[N], dep[N];
void dfs1(int u, int fa) {
for (auto t : g[u]) {
int v = t.first, id = t.second;
if (fa == v) continue;
if (vise[id]) continue;
vise[id] = true;
if (vis[v]) {
++ w[u], -- w[v];
}
else {
vis[v] = true;
dfs1(v, u);
tr[u].emplace_back(v, id);
st[id] = true;
}
}
}
void dfs2(int u) {
for (auto t : tr[u]) {
int v = t.first;
dep[v] = dep[u] + 1;
dfs2(v);
w[u] += w[v];
}
if (u != 1 && !w[u]) {
puts("0");
exit(0);
}
}
int main() {
cin >> n >> m;
for (int i = 1, u, v; i <= m; ++ i ) {
cin >> u >> v;
edges[i] = {u, v, i};
g[u].emplace_back(v, i), g[v].emplace_back(u, i);
}
vis[1] = true, dep[1] = 1, dfs1(1, -1), dfs2(1);
for (int i = 1; i <= m; ++ i ) {
int u = edges[i].a, v = edges[i].b;
if (st[i]) {
if (dep[u] < dep[v]) swap(u, v);
}
else {
if (dep[v] < dep[u]) swap(u, v);
}
cout << u << ' ' << v << '\n';
}
return 0;
}
\(\color{#9D3DCF}(8)\) CF76A Gift
- 一张图,每条边有两个属性 \((g_i, s_i)\)。给定 \(G, S\),求一棵图的生成树 \(T\),使得 \(G \times \max(g_i) + S \times \max (s_i)\) 最小(\(i \in T\))。
- \(n \le 200\),\(m \le 5 \times 10^4\)。
枚举 \(i\) 并加入所有 \(g_j \le g_i\) 的边 \(j\),这样就固定了 \(g_i\) 是最大值。
接下来我们将刚才加入的边按照 \(s_i\) 跑最小生成树,然后就能轻易地计算答案了。
此时复杂度为 \(\Theta(m^2 \log m)\),无法通过。
可以发现将边按照 \(g_i\) 从小到大排序后,每次加入一条新的边时,我们只需要将上一轮的 MST 中的 \(n -1\) 条边与这条边结合,从而计算新的 MST,而不需要将前 \(i\) 条边全部重新计算。因此复杂度降到了 \(\Theta(nm \log n)\)。
$\color{blue}\text{Code}$
int n, m, G, S, res = 2e18;
struct Edge {
int u, v, g, s;
}t[N];
vector<int> edges;
struct BCJ {
int p[N];
void init() { for (int i = 1; i <= n; ++ i ) p[i] = i; }
int fifa(int x) { return x == p[x] ? x : p[x] = fifa(p[x]); }
void merge(int x, int y) { p[fifa(x)] = fifa(y); }
bool chk(int a, int b) { return fifa(a) == fifa(b); }
}BC;
void Luogu_UID_748509() {
fin >> n >> m >> G >> S;
for (int i = 1; i <= m; ++ i ) {
int a, b, c, d;
fin >> a >> b >> c >> d;
t[i] = {a, b, c, d};
}
sort(t + 1, t + m + 1, [&](Edge x, Edge y) {
return x.g < y.g;
});
for (int i = 1; i <= m; ++ i ) {
edges.push_back(i);
sort(edges.begin(), edges.end(), [&](int x, int y) {
return t[x].s < t[y].s;
});
BC.init();
vector<int> cur;
int k = 0;
for (int j : edges) {
int a = t[j].u, b = t[j].v;
if (!BC.chk(a, b)) {
cur.push_back(j);
BC.merge(a, b);
k = max(k, t[j].s);
}
}
if (cur.size() == n - 1) res = min(res, G * t[i].g + S * k);
edges = cur;
}
if (res == 2e18) res = -1;
fout << res;
}
\(\color{#52A41A}(9)\) CF711D Directed Roads
有 \(n\) 个点和 \(n\) 条边,第 \(i\) 条边从 \(i\) 连到 \(a_i\)(保证 \(i \ne a_i\))。 每条边需要指定一个方向(无向边变为有向边)。问有多少种指定方向的方案使得图中不出现环,答案对 \(10^9 + 7\) 取模。
\(n \le 2 \times 10^5\)。
显然图构成了若干棵互不干涉的基环树。那么我们对于每一棵基环树单独考虑,相乘即为答案。
若第 \(i\) 棵基环树中有 \(p_i\) 条边在环上,\(q_i\) 条边不在换上。首先显然有 \(\sum p_i + q_i = n\)。
考虑定向后出现环的条件,是当前这 \(p_i\) 条边的指向全部相同,即存在 \(2\) 中存在环的方案。所以不出现环的方案数即 \((2^{p_i} - 2) \times 2^{q_i}\)。
$\color{blue}\text{Code}$
int n, a[N], id[N], sum;
vector<int> vec;
int vis[N];
void dfs(int u, int t) {
id[u] = t;
vis[u] = 1;
if (!vis[a[u]]) dfs(a[u], t + 1);
else if (vis[a[u]] == 1) {
int w = t - id[a[u]] + 1;
vec.push_back(w);
sum -= w;
}
vis[u] = 2;
}
int fpm(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % P;
b >>= 1, a = (ll)a * a % P;
}
return res;
}
void Luogu_UID_748509() {
fin >> n;
for (int i = 1; i <= n; ++ i ) fin >> a[i];
sum = n;
for (int i = 1; i <= n; ++ i )
if (!id[i])
dfs(i, 1);
int res = fpm(2, sum);
for (int t : vec) res = (ll)res * (fpm(2, t) - 2) % P;
fout << res;
}
\(\color{#3498D8}(10)\) CF85E Guard Towers
- 在直角坐标系上有 \(n\) 座塔。要求把这些塔分成两组,使得同组内的两座塔的曼哈顿距离的最大值最小,并求出在此前提下求出有多少种分组方案,对 \(10^9 + 7\) 取模。
- \(n, x_i, y_i \le 5 \times 10^3\)。
首先二分答案。然后以平方的复杂度暴力将不满足条件的塔之间连边。此时,若图形成了一张二分图,那么答案可行。这是第一问。
在这张二分图中会呈现若干个连通块,每个连通块显然后两种黑白染色的方案,即将点分成两组的方案。那么答案即 \(2\) 的连通块数量的幂。这是第二问。
$\color{blue}\text{Code}$
int n, a[N], b[N];
struct Gragh {
vector<int> g[N];
void clear() { for (int i = 1; i <= n; ++ i ) g[i].clear(); }
void add(int a, int b) { g[a].push_back(b); }
int col[N];
int dfs(int u, int c) {
col[u] = c;
int cnt = 1;
for (int v : g[u]) {
if (!col[v]) {
int t = dfs(v, 3 - c);
if (t == -1) return -1;
cnt += t;
}
else if (col[v] == c) return -1;
}
return cnt;
}
int dsu() {
fill(col + 1, col + n + 1, 0);
int res = 1;
for (int i = 1; i <= n; ++ i )
if (!col[i]) {
int t = dfs(i, 1);
if (t == -1) return -1;
res = res * 2ll % P;
}
return res;
}
}G;
int chk(int mid) {
G.clear();
for (int i = 1; i <= n; ++ i )
for (int j = i + 1; j <= n; ++ j )
if (abs(a[i] - a[j]) + abs(b[i] - b[j]) > mid)
G.add(i, j), G.add(j, i);
return G.dsu();
}
void Luogu_UID_748509() {
fin >> n;
for (int i = 1; i <= n; ++ i ) {
fin >> a[i] >> b[i];
}
int l = 0, r = 1e4, res1 = 0, res2 = 0;
while (l <= r) {
int mid = l + r >> 1;
int t = chk(mid);
if (t == -1) l = mid + 1;
else r = mid - 1, res1 = mid, res2 = t;
}
fout << res1 << '\n' << res2 << '\n';
}
\(\color{#9D3DCF}(11)\) CF732F Tourist Reform
- 给定一张 \(n\) 个点 \(m\) 条边的简单无向图,你需要给每条边都确定一个方向,使原图变成一个有向图。设 \(R_i\) 为从 \(i\) 号点出发能到达的不同点的数量。最大化所有 \(R_i\) 的最小值。
- 输出这个最小值以及每条边的定向方案。
- \(n , m \le 4 \times 10^5\)。
首先根据 CF118E 的思路,一定存在一种为一个 dcc(边双连通分量)中所有边定向的方案,使其成为一个 scc(强连通分量)。具体见 \(\color{#3498D8}(7)\)。
所以将所有 dcc 缩点,那么原图将成为一颗树,每个点的点权为这个点所代表的 dcc 的点数。接下来最优的构造方案是将点权最大的点作为这棵树的根,然后让其余边都从儿子指向父亲。容易证明这样是正确的。
$\color{blue}\text{Code}$
int n, m;
vector<int> dcc[N];
int dcc_cnt, dep[N];
bool edges[N];
pair<int, int> p[N];
struct Gragh {
vector<pair<int, int> > g[N];
void add(int a, int b, int c) {
g[a].emplace_back(b, c);
g[b].emplace_back(a, c);
}
int dfn[N], low[N], ts, stk[N], top;
bool is_bridge[N];
void Tarjan_dfs(int u, int from) {
dfn[u] = low[u] = ++ ts;
stk[ ++ top] = u;
for (auto t : g[u]) {
int v = t.first, i = t.second;
if (!dfn[v]) {
Tarjan_dfs(v, i);
low[u] = min(low[u], low[v]);
if (dfn[u] < low[v]) is_bridge[i] = true;
}
else if (i != from) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
++ dcc_cnt;
int y;
do {
y = stk[top -- ];
dcc[dcc_cnt].push_back(y);
} while (y != u);
}
}
void Tarjan() {
Tarjan_dfs(1, -1);
}
bool st[N], vis[N];
void dfs(int u) {
st[u] = true;
for (auto t : g[u]) {
int v = t.first, i = t.second;
if (vis[i]) continue;
vis[i] = true;
if (st[v]) {
edges[i] = true;
}
else {
edges[i] = false;
dep[v] = dep[u] + 1;
dfs(v);
}
}
}
}G;
void Luogu_UID_748509() {
fin >> n >> m;
for (int i = 1, a, b; i <= m; ++ i ) {
fin >> a >> b;
G.add(a, b, i), G.add(b, a, i);
p[i].first = a, p[i].second = b;
}
G.Tarjan();
int k = 0;
for (int i = 1; i <= dcc_cnt; ++ i )
if (dcc[i].size() > dcc[k].size())
k = i;
G.dfs(dcc[k].back());
fout << dcc[k].size() << '\n';
for (int i = 1; i <= m; ++ i ) {
int a = p[i].first, b = p[i].second;
if (G.is_bridge[i]) {
if (dep[a] < dep[b]) swap(a, b);
}
else if (edges[i]) {
if (dep[a] > dep[b]) swap(a, b);
}
else {
if (dep[a] < dep[b]) swap(a, b);
}
fout << a << ' ' << b << '\n';
}
}
\(\color{#9D3DCF}(12)\) CF746G New Roads
- 构造一棵 \(n\) 个点的深度为 \(t\) 的树,以 \(1\) 为根,使其中深度为 \(i\) 的点有 \(a_i\) 个且叶节点有 \(k\) 个。或报告无解。
- \(t, k \le n \le 2 \times 10^5\)。
为了方便,我们令根节点的深度为 \(1\)。所有读入都向后顺延一位。
首先计算这棵树最多和最少有几个叶子节点,那么如果 \(k\) 不在这个范围内则无解。那么模拟样例二:
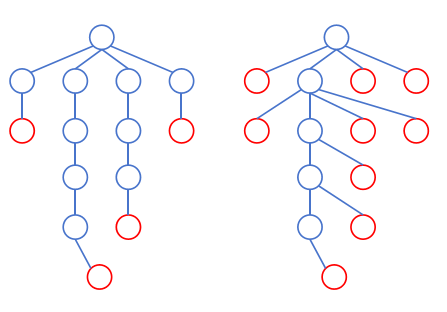
第一个观察是无论如何构造,最后一层的节点一定是叶子节点,且第一层一定不是叶节点。
可以发现叶子最多的情况,是每一层的节点都连向上一层的同一个节点,即 \(k_{\max} = a_t + \sum_{i=1}^{t-1} (a_i - 1)\)。叶子最少的情况,是每一层的节点都尽可能多的连向上一层的不同的点,直到不能连为止,即 \(k_{\min} = a_t + \sum_{i=1}^{t-1}\max(a_i - a_{i + 1}, 0)\)。
除第一层外和最后一层外,每一层的叶子节点数一定不会少于 \(a_i - a_{i + 1}\)(如左图)且不会超过 \(a_i - 1\)(如右图)。那么我们可以处理出 \(b_2, b_3, \dots, b_{t - 1}\) 表示我们将要在第 \(i\) 层构造出 \(b_i\) 个叶子节点。需要保证 \(\max(0, a_i - a_{i + 1}) \le b_i \le a_i - 1\) 且 \(\sum_{i=2}^{t-1} b_i = k - a_t\)。这是极易做到的。
然后考虑根据 \(b\) 数组构造整棵树。显然我们需要满足第 \(i\) 层中有 \(a_i - b_i\) 个点不是叶子节点,即连接至少一个下一层的点。那么直接模拟构造即可。
$\color{blue}\text{Code}$
int n, k, t, a[N], sum[N];
int Id(int a, int b) { // 第 a 层的第 b 个点
return sum[a - 1] + b;
}
int mn() {
int res = a[t];
for (int i = 1; i < t; ++ i )
if (a[i] > a[i + 1]) res += a[i] - a[i + 1];
return res;
}
int mx() {
int res = a[t];
for (int i = 1; i < t; ++ i )
res += a[i] - 1;
return res;
}
int b[N];
vector<pair<int, int> > res;
void build_b() {
int lst = k - a[t];
for (int i = 2; i < t; ++ i ) {
b[i] = max(0ll, a[i] - a[i + 1]);
lst -= b[i];
}
for (int i = 2; i < t; ++ i ) {
int tmp = min(lst, a[i] - 1 - b[i]);
b[i] += tmp;
lst -= tmp;
}
}
void Luogu_UID_748509() {
fin >> n >> t >> k;
++ t;
sum[1] = 1;
a[1] = 1;
for (int i = 2; i <= t; ++ i ) fin >> a[i], sum[i] = sum[i - 1] + a[i];
if (k < mn() || k > mx()) puts("-1");
else {
build_b();
for (int i = 1; i < t; ++ i ) {
int x = a[i] - b[i];
for (int j = 1; j <= x; ++ j )
res.emplace_back(Id(i, j), Id(i + 1, j));
for (int j = x + 1; j <= a[i + 1]; ++ j )
res.emplace_back(Id(i, x), Id(i + 1, j));
}
fout << n << '\n';
for (auto t : res) fout << t.first << ' ' << t.second << '\n';
}
}
\(\color{#3498D8}(13)\) CF698B Fix a Tree
对于一棵大小为 \(n\) 的有根树,我们定义 \(f_i\):
- 对于非根节点 \(i\) 有 \(f_i=fa_i\),也就是 \(i\) 的父节点。
- 对于根节点 \(root\),有 \(f_{root}=root\)。
这样的 \(f\) 数组对应了一棵有根树。
现给你一个长度为 \(n\) 的数组 \(a\),你需要修改尽量少的数组元素,使得该数组能够对应一棵有根树。
\(a_i \le n \le 2 \times 10^5\)。
显然原图构成了若干棵树和基环树。我们要做的是将它们合并。
首先我们可以钦定一个点作为根节点。若原图中存在 \(a_i = i\) 的情况,就把这个 \(i\) 钦定为根。反之如果不存在,就随便找一个环,并钦定环上某个点为根即可。
然后对于每个环,我们希望破坏这个环使得整个图成为树。那么任选其中一个点,并将这个点指向根即可。
$\color{blue}\text{Code}$
int n, a[N], f[N], st[N], cnt, root;
void dfs(int u, int cnt) {
st[u] = cnt;
if (f[u] == u) {
if (!root) root = u;
else f[u] = root;
}
else if (st[f[u]]) {
if (st[f[u]] == cnt) {
if (!root) {
root = u;
f[u] = u;
}
else f[u] = root;
}
}
else dfs(f[u], cnt);
}
void Luogu_UID_748509() {
fin >> n;
for (int i = 1; i <= n; ++ i ) {
fin >> a[i];
f[i] = a[i];
if (i == f[i]) root = i;
}
for (int i = 1; i <= n; ++ i )
if (!st[i]) dfs(i, ++ cnt);
int res = 0;
for (int i = 1; i <= n; ++ i ) res += a[i] != f[i];
fout << res << '\n';
for (int i = 1; i <= n; ++ i ) fout << f[i] << ' ';
}
\(\color{#52A41A}(14)\) P2296 [NOIP2014 提高组] 寻找道路
在有向图 \(G\) 中,每条边的长度均为 \(1\),现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
路径上的所有点的出边所指向的点都直接或间接与终点连通。
在满足条件 \(1\) 的情况下使路径最短。
注意:图 \(G\) 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
\(n \le 10^4\),\(m \le 2 \times 10^5\)。
显然的想法是,我们将所有满足「所有出边所指向的点都直接或间接与 \(t\) 连通」的点拿出来建图,然后求 \(s\) 到 \(t\) 的最短路即可。问题是如何找到这些点。
首先可以建反图,从 \(t\) 开始 dfs,求出所有能到达 \(t\) 的点并标记。然后枚举每一个点,检查它的出边能否都被标记即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 10010, M = 200010;
int n, m, s, t;
struct Graph {
int h[N], e[M], ne[M], idx = 1;
void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ; }
}A, B;
bool st[N], can[N], vis[N];
int dis[N];
void dfs(int u) {
if (!st[u]) {
st[u] = true;
for (int i = B.h[u]; i; i = B.ne[i]) {
int v = B.e[i];
dfs(v);
}
}
return;
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; ++ i ) {
int u, v;
cin >> u >> v;
if (u != v) {
A.add(u, v);
B.add(v, u);
}
}
cin >> s >> t;
dfs(t);
for (int u = 1; u <= n; ++ u ) {
can[u] = true;
for (int i = A.h[u]; i; i = A.ne[i]) {
int v = A.e[i];
if (!st[v]) can[u] = false;
}
}
if (!can[s]) return puts("-1"), 0;
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
vis[s] = 1;
queue<int> q;
q.push(s);
while (q.size()) {
int u = q.front();
q.pop();
for (int i = A.h[u]; i; i = A.ne[i]) {
int v = A.e[i];
if (!vis[v] && can[v]) {
vis[v] = true;
q.push(v);
dis[v] = dis[u] + 1;
}
}
}
cout << (dis[t] > 1e9 ? -1 : dis[t]) << '\n';
return 0;
}

