数论做题笔记
- 给定
个元素的集合 和整数 。求有多少组 个集合 使得 且 。 。
首先考虑
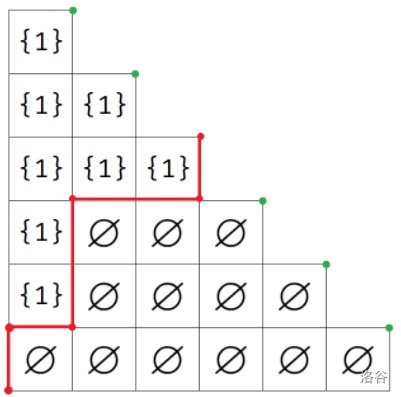
那么答案显然为轮廓线的数量,也即从左下角往右上走,且只能向上或向右,最终到达图中绿点的方案数。总步数为
考虑更普遍的
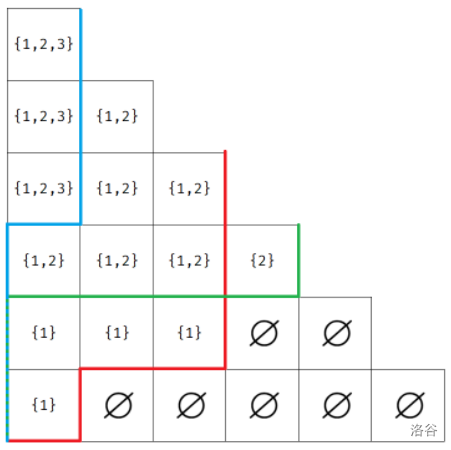
那么答案即为
int fpm(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % P;
b >>= 1, a = (ll)a * a % P;
}
return res;
}
void Luogu_UID_748509() {
int a, b;
fin >> a >> b;
fout << fpm(2, a * b) << '\n';
}
组询问。每次给定 ,求有多少正整数 使得 且 。 , 。
对于一个质数
那么我们可以对于
通过
此时发现通过这两个条件可以推出两个
int a0, a1, b0, b1;
map<int, int> primes[4];
set<int> S;
void init(int x, int id) {
for (int i = 2; i <= x / i; ++ i )
if (x % i == 0) {
S.insert(i);
while (x % i == 0) {
++ primes[id][i];
x /= i;
}
}
if (x > 1) {
S.insert(x);
++ primes[id][x];
}
}
struct Range {
int l, r;
Range operator +(const Range &h) const {
return {max(l, h.l), min(r, h.r)};
}
};
Range calcmin(int a, int b) {
// min(a, x) == b,x 的范围?
if (a < b) return {INF, -INF};
if (a == b) return {a, INF};
return {b, b};
}
Range calcmax(int a, int b) {
// max(a, x) == b,x 的范围?
if (a > b) return {INF, -INF};
if (a == b) return {-INF, a};
return {b, b};
}
void Luogu_UID_748509() {
S.clear();
for (int i : {0, 1, 2, 3}) primes[i].clear();
fin >> a0 >> a1 >> b0 >> b1;
init(a0, 0), init(a1, 1), init(b0, 2), init(b1, 3);
int res = 1;
for (int p : S) {
auto range = calcmin(primes[0][p], primes[1][p]) + calcmax(primes[2][p], primes[3][p]);
res *= max(0ll, range.r - range.l + 1);
}
fout << res << '\n';
return;
}
组询问,给定 ,求 。 , 。
令
根据扩展欧拉定理可得:
很显然
即:
可以发现
边界显然
int fpm(int a, int b, int P) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % P;
b >>= 1, a = (ll)a * a % P;
}
return res;
}
int p[N], cnt, phi[N];
bool st[N];
void init(int n) {
phi[1] = 1;
for (int i = 2; i <= n; ++ i ) {
if (!st[i]) phi[i] = i - 1, p[ ++ cnt] = i;
for (int j = 1; p[j] <= n / i; ++ j ) {
st[p[j] * i] = true;
if (i % p[j] == 0) {
// p[j] 是 i 的最小质因子
phi[p[j] * i] = phi[i] * p[j];
break;
}
phi[p[j] * i] = phi[i] * (p[j] - 1);
}
}
}
int solve(int p) {
if (p == 1) return 0;
return fpm(2, solve(phi[p]) + phi[p], p);
}
void Luogu_UID_748509() {
int x;
fin >> x;
fout << solve(x) << '\n';
}
- 给定一个多项式
,请求出多项式展开后 项的系数。 , , 。
首先视
显然
因为
int a, b, k, n, m;
int fpm(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % P;
b >>= 1, a = (ll)a * a % P;
}
return res;
}
int C(int a, int b) {
int res = 1;
for (int i = a - b + 1; i <= a; ++ i ) res = res * i % P;
for (int i = 1; i <= b; ++ i ) res = res * fpm(i, P - 2) % P;
return res;
}
void Luogu_UID_748509() {
fin >> a >> b >> k >> n >> m;
fout << C(k, n) * fpm(a, n) % P * fpm(b, m) % P << '\n';
}
- 给定
个数 。 次查询 。 , 。
对于
同理,对于
回到题目。仿照 HH 的项链 的思路,我们可以将
int n, q, a[N];
struct Query {
int l, r, id;
bool operator <(const Query &h) const {
return r == h.r ? l < h.l : r < h.r;
}
}que[N];
int res[N];
int fpm(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (ll)res * a % P;
b >>= 1, a = (ll)a * a % P;
}
return res;
}
int calc(int p) {
return (ll)(p - 1) * fpm(p, P - 2) % P;
}
struct Segment_Tree {
struct Node {
int l, r, v;
}tr[N << 2];
void pushup(int u) {
tr[u].v = (ll)tr[u << 1].v * tr[u << 1 | 1].v % P;
}
void build(int u, int l, int r, bool op) {
tr[u] = {l, r};
if (l == r) tr[u].v = op ? 1ll : a[l] % P;
else {
int mid = l + r >> 1;
build(u << 1, l, mid, op), build(u << 1 | 1, mid + 1, r, op);
pushup(u);
}
}
void modify(int u, int x, int d) {
if (tr[u].l == tr[u].r) tr[u].v = d;
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(u << 1, x, d);
else modify(u << 1 | 1, x, d);
pushup(u);
}
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 1;
if (l <= mid) res = query(u << 1, l, r);
if (r > mid) res = (ll)res * query(u << 1 | 1, l, r) % P;
return res;
}
void modify(int x, int d) {
int t = query(1, x, x);
if (d > 0) modify(1, x, (ll)t * d % P);
else modify(1, x, (ll)t * fpm(-d, P - 2) % P);
}
int query(int l, int r) {
return query(1, l, r);
}
}A, B;
vector<int> primes(int x) {
vector<int> res;
for (int j = 2; j <= x / j; ++ j )
if (x % j == 0) {
res.push_back(j);
while (x % j == 0) x /= j;
}
if (x > 1) res.push_back(x);
return res;
}
int lst[M];
void Luogu_UID_748509() {
fin >> n;
for (int i = 1; i <= n; ++ i ) fin >> a[i];
A.build(1, 1, n, 0), B.build(1, 1, n, 1);
fin >> q;
for (int i = 1; i <= q; ++ i ) {
fin >> que[i].l >> que[i].r;
que[i].id = i;
res[i] = A.query(que[i].l, que[i].r);
}
sort(que + 1, que + q + 1);
for (int i = 1, j = 1; i <= q; ++ i ) {
for (; j <= que[i].r; ++ j ) {
auto v = primes(a[j]);
for (int p : v) {
if (lst[p]) B.modify(lst[p], -calc(p));
lst[p] = j;
B.modify(j, calc(p));
}
}
res[que[i].id] = (ll)res[que[i].id] * B.query(que[i].l, que[i].r) % P;
}
for (int i = 1; i <= q; ++ i ) fout << res[i] << '\n';
return;
}
- 给定
,求 。 。
首先根据取模的定义可知
然后发现
注意当
int n, m, res;
int mod(int x) {
return x % P;
}
int calc(int l, int r) {
return mod(l + r) * mod(r - l + 1) % P * 500000004ll % P;
}
void Luogu_UID_748509() {
fin >> n >> m;
int res = mod(n) * mod(m) % P;
for (int l = 1, r; l <= min(n, m); l = r + 1) {
r = min(n / (n / l), m);
// cout << l << ' ' << r << ' ' << (n / l) % P << ' ' << (r - l + 1) % P << '\n';
res = ((res - mod(n / l) * calc(l, r) % P) % P + P) % P;
}
fout << res;
}
- 求
。 。
推式子。
线性筛
int p[N]; // p[i] 表示第 i 个质数
bool st[N]; // st[i] 表示 i 是否是质数
int phi[N]; // phi[i] 表示 φ(i) 的值
int cnt;
void prime(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; i ++ )
{
if (!phi[i]) p[ ++ cnt] = i, phi[i] = i - 1;
for (int j = 1; j <= cnt && p[j] <= n / i; j ++ )
{
if (i % p[j]) phi[i * p[j]] = phi[i] * phi[p[j]]; // p[j] 不是 i 的最小质因子
else // p[j] 是 i 的最小质因子
{
phi[i * p[j]] = phi[i] * (p[j]);
break;
}
}
}
}
void Luogu_UID_748509() {
int n; fin >> n;
prime(n);
int res = 0;
for (int i = 1; i <= n; ++ i ) res += phi[i] * (n / i) * (n / i);
fout << res;
}



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现