线段树做题笔记
\(\color{#3498D8}(1)\) P4145 上帝造题的七分钟 2 / 花神游历各国
- 区间开根,区间求和。
注意到对于一个 \(10^{12}\) 的数而言,最多开根 \(6\) 次就会变成 \(1\)。接下来在开根都不会发生变化了。
所以修改时我们可以维护区间最大值。如果区间最大值小于等于 \(1\),那么直接将这个区间跳过。否则暴力递归处理两个儿子。
$\color{blue}\text{Code}$
#include <iostream>
#include <cmath>
using namespace std;
#define int long long
const int N = 1000010;
int n, m, a[N], k, l, r;
#define ls (u << 1)
#define rs (u << 1 | 1)
struct Tree
{
int l, r, v, mx;
}tr[N << 2];
void pushup(int u)
{
tr[u].v = tr[ls].v + tr[rs].v;
tr[u].mx = max(tr[ls].mx, tr[rs].mx);
}
void build(int u, int l, int r)
{
tr[u] = {l, r};
if (l == r) tr[u].v = tr[u].mx = a[l];
else
{
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
pushup(u);
}
}
void modify(int u, int l, int r)
{
if (tr[u].l == tr[u].r) tr[u].v = tr[u].mx = sqrt(tr[u].v);
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid && tr[ls].mx != 1) modify(ls, l, r);
if (r > mid && tr[rs].mx != 1) modify(rs, l, r);
pushup(u);
}
}
int query(int u, int l, int r)
{
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 0;
if (l <= mid) res = query(ls, l, r);
if (r > mid) res += query(rs, l, r);
return res;
}
main()
{
cin >> n;
for (int i = 1; i <= n; ++ i ) cin >> a[i];
build(1, 1, n);
cin >> m;
while (m -- )
{
cin >> k >> l >> r;
if (l > r) swap(l, r);
if (k) cout << query(1, l, r) << '\n';
else modify(1, l, r);
}
return 0;
}
\(\color{#BFBFBF}(2)\) UOJ 228 基础数据结构练习题
- 维护操作:
- \(\forall i \in [l, r], a_i \gets a_i + k\);
- \(\forall i \in [l, r], a_i \gets \lfloor \sqrt{a_i} \rfloor\);
- 查询 \(\sum_{i=l}^r a_i\)。
对于一个区间 \([l, r]\),如果将这个区间全部开根,那么极差一定也会至少开根。
如果令原最大值最小值为 \(x, y\),那么可以推出 \(\sqrt x - \sqrt y \le \sqrt{x - y}\)。所以我们要在极差上做处理。
当我们需要对一个线段树上的区间节点 \([l, r]\) 且最大最小值为 \(x, y\) 做开根时,如果 \(x - y = \lfloor \sqrt x \rfloor - \lfloor \sqrt y \rfloor\),那么开根操作可以转化为减 \(x - \lfloor \sqrt x \rfloor\)。否则,暴力递归到左右儿子分别处理。
所以维护区间最大值、最小值、和。可以证明这样做的复杂度是正确的。
注意开根下取整。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 100010;
int n, m, a[N], op, l, r, x;
struct Tree {
int l, r, v, add, mx, mn;
}tr[N << 2];
void pushup(int u) {
tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
tr[u].mx = max(tr[u << 1].mx, tr[u << 1 | 1].mx);
tr[u].mn = min(tr[u << 1].mn, tr[u << 1 | 1].mn);
return;
}
void calc(int u, int d) {
tr[u].add += d;
tr[u].v += (tr[u].r - tr[u].l + 1) * d;
tr[u].mn += d;
tr[u].mx += d;
return;
}
void pushdown(int u) {
calc(u << 1, tr[u].add);
calc(u << 1 | 1, tr[u].add);
tr[u].add = 0;
return;
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) tr[u].v = tr[u].mx = tr[u].mn = a[l];
else {
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
return;
}
void add(int u, int l, int r, int x) {
if (tr[u].l >= l && tr[u].r <= r) calc(u, x);
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) add(u << 1, l, r, x);
if (r > mid) add(u << 1 | 1, l, r, x);
pushup(u);
}
return;
}
int F(int x) {
return sqrt(x);
}
void modify(int u, int l, int r) {
if (tr[u].l == tr[u].r) {
tr[u].mn = tr[u].mx = tr[u].v = sqrt(tr[u].v);
tr[u].add = 0;
}
else if (tr[u].l >= l && tr[u].r <= r && tr[u].mx - F(tr[u].mx) == tr[u].mn - F(tr[u].mn)) {
calc(u, F(tr[u].mx) - tr[u].mx);
}
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) modify(u << 1, l, r);
if (r > mid) modify(u << 1 | 1, l, r);
pushup(u);
}
return;
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 0;
pushdown(u);
if (l <= mid) res = query(u << 1, l, r);
if (r > mid) res += query(u << 1 | 1, l, r);
pushup(u);
return res;
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++ i ) {
scanf("%lld", a + i);
}
build(1, 1, n);
while (m -- ) {
scanf("%lld%lld%lld", &op, &l, &r);
if (op == 1) {
scanf("%lld", &x);
add(1, l, r, x);
}
else if (op == 2) {
modify(1, l, r);
}
else {
printf("%lld\n", query(1, l, r));
}
}
return 0;
}
\(\color{#BFBFBF}(3)\) LOJ 6029 市场
维护操作:
- \(\forall i \in [l, r], a_i \gets a_i + k\);
- \(\forall i \in [l, r], a_i \gets \lfloor \frac{a_i}d \rfloor\);
- 查询 \(\min_{i=l}^r a_i\)。
- 查询 \(\sum_{i=l}^r a_i\)。
同上题思路。注意负数下取整。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 100010;
int n, m, a[N], op, l, r, x;
struct Tree {
int l, r, v, add, mx, mn;
}tr[N << 2];
void pushup(int u) {
tr[u].v = tr[u << 1].v + tr[u << 1 | 1].v;
tr[u].mx = max(tr[u << 1].mx, tr[u << 1 | 1].mx);
tr[u].mn = min(tr[u << 1].mn, tr[u << 1 | 1].mn);
return;
}
void calc(int u, int d) {
tr[u].add += d;
tr[u].v += (tr[u].r - tr[u].l + 1) * d;
tr[u].mn += d;
tr[u].mx += d;
return;
}
void pushdown(int u) {
calc(u << 1, tr[u].add);
calc(u << 1 | 1, tr[u].add);
tr[u].add = 0;
return;
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l == r) tr[u].v = tr[u].mx = tr[u].mn = a[l];
else {
int mid = l + r >> 1;
build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
pushup(u);
}
return;
}
void add(int u, int l, int r, int x) {
if (tr[u].l >= l && tr[u].r <= r) calc(u, x);
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) add(u << 1, l, r, x);
if (r > mid) add(u << 1 | 1, l, r, x);
pushup(u);
}
return;
}
int F(int x, int y) {
return floor(1.0 * x / y);
}
void modify(int u, int l, int r, int x) {
if (tr[u].l == tr[u].r) {
tr[u].mn = tr[u].mx = tr[u].v = F(tr[u].v, x);
}
else if (tr[u].l >= l && tr[u].r <= r && tr[u].mx - F(tr[u].mx, x) == tr[u].mn - F(tr[u].mn, x)) {
calc(u, F(tr[u].mx, x) - tr[u].mx);
}
else {
int mid = tr[u].l + tr[u].r >> 1;
pushdown(u);
if (l <= mid) modify(u << 1, l, r, x);
if (r > mid) modify(u << 1 | 1, l, r, x);
pushup(u);
}
return;
}
int sum(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 0;
pushdown(u);
if (l <= mid) res = sum(u << 1, l, r);
if (r > mid) res += sum(u << 1 | 1, l, r);
pushup(u);
return res;
}
int minn(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].mn;
int mid = tr[u].l + tr[u].r >> 1, res = 1e18;
pushdown(u);
if (l <= mid) res = minn(u << 1, l, r);
if (r > mid) res = min(res, minn(u << 1 | 1, l, r));
pushup(u);
return res;
}
signed main() {
scanf("%lld%lld", &n, &m);
for (int i = 1; i <= n; ++ i ) {
scanf("%lld", a + i);
}
build(1, 1, n);
while (m -- ) {
scanf("%lld%lld%lld", &op, &l, &r);
++ l, ++ r;
if (op == 1) {
scanf("%lld", &x);
add(1, l, r, x);
}
else if (op == 2) {
scanf("%lld", &x);
if (x != 1) modify(1, l, r, x);
}
else if (op == 3) {
printf("%lld\n", minn(1, l, r));
}
else {
printf("%lld\n", sum(1, l, r));
}
}
return 0;
}
\(\color{#3498D8}(4)\) CF935E Fafa and Ancient Mathematics
-
给出一个算式,由括号和小于 \(10\) 的正整数和问号组成。每个问号可以改为加号或减号。
求如果总共填 \(p\) 个加号和 \(m\) 个减号,求算式的最大值。
-
\(n \le 10^4\),\(\min(p, m) \le 100\)。
建表达式树。如 \(((1 + 2) - ((3 - 4) + 5))\):
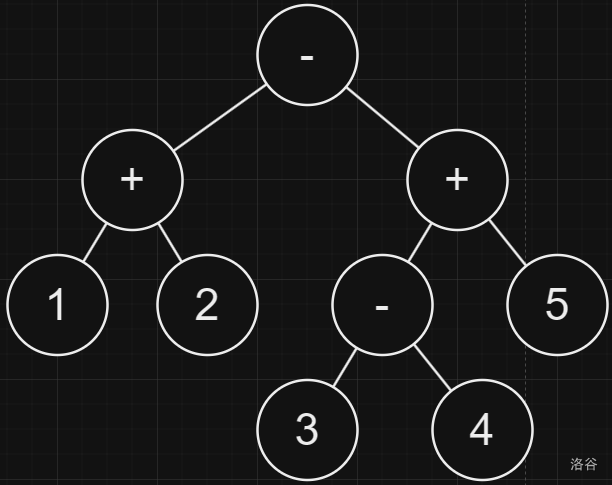
然后设 DP 状态 \(f_{u, k}\) 和 \(g_{u, k}\) 分别表示以 \(u\) 为根的子树中,如果用 \(k\) 个加号/减号,代数式的最大值是多少。具体是加号/减号可以看 \(p, m\) 谁更小,因为题目保证 \(\min(p, m) \le 100\) 所以这样设状态是可行的。
转移时枚举 \(u\) 选择加号/减号,左子树用了几个加号/减号,那么右子树的加号/减号数量是可以被计算的。然后转移即可。
$\color{blue}\text{Code}$
const int N = 20010;
char s[N];
int n, a, b;
struct Tree {
int l, r, v;
}tr[N];
int idx;
int l[N], r[N];
long long f[N][110], g[N][110];
map<int, vector<int> > pos;
int sum[N];
int que[N];
inline int build(const int ll, const int rr) {
const int u = ++ idx;
tr[u] = {ll, rr};
if (ll == rr) f[u][0] = g[u][0] = s[ll] - '0';
else {
register int x = *lower_bound(pos[sum[ll - 1] + 1].begin(), pos[sum[ll - 1] + 1].end(), ll);
tr[u].v = que[rr] - que[ll - 1];
l[u] = build(ll + 1, x - 1);
r[u] = build(x + 1, rr - 1);
}
return u;
}
inline void dfsa(const int u) {
if (tr[u].l == tr[u].r) return;
dfsa(l[u]), dfsa(r[u]);
for (register int i = 0; i <= tr[u].v; ++ i )
for (register int j = 0; j <= tr[l[u]].v; ++ j ) {
if (i - j - 1 <= tr[r[u]].v && i - j - 1 >= 0)
f[u][i] = max(f[u][i], f[l[u]][j] + f[r[u]][i - j - 1]),
g[u][i] = min(g[u][i], g[l[u]][j] + g[r[u]][i - j - 1]);
if (i - j <= tr[r[u]].v && i - j >= 0)
f[u][i] = max(f[u][i], f[l[u]][j] - g[r[u]][i - j]),
g[u][i] = min(g[u][i], g[l[u]][j] - f[r[u]][i - j]);
}
return;
}
inline void dfsb(const int u) {
if (tr[u].l == tr[u].r) return;
dfsb(l[u]), dfsb(r[u]);
for (register int i = 0; i <= tr[u].v; ++ i )
for (register int j = 0; j <= tr[l[u]].v; ++ j ) {
if (i - j - 1 <= tr[r[u]].v && i - j - 1 >= 0)
f[u][i] = max(f[u][i], f[l[u]][j] - g[r[u]][i - j - 1]),
g[u][i] = min(g[u][i], g[l[u]][j] - f[r[u]][i - j - 1]);
if (i - j <= tr[r[u]].v && i - j >= 0)
f[u][i] = max(f[u][i], f[l[u]][j] + f[r[u]][i - j]),
g[u][i] = min(g[u][i], g[l[u]][j] + g[r[u]][i - j]);
}
return;
}
signed main() {
memset(f, -0x3f, sizeof f);
memset(g, 0x3f, sizeof g);
scanf("%s%d%d", s + 1, &a, &b);
n = strlen(s + 1);
pos[0].push_back(0);
for (int i = 1; i <= n; ++ i ) {
sum[i] = sum[i - 1];
sum[i] += s[i] == '(';
sum[i] -= s[i] == ')';
if (s[i] == '?') pos[sum[i]].push_back(i);
que[i] = que[i - 1] + (s[i] == '?');
}
build(1, n);
if (a <= b) {
dfsa(1);
printf("%lld\n", f[1][a]);
}
else {
dfsb(1);
printf("%lld\n", f[1][b]);
}
return 0;
}
\(\color{#9D3DCF}(5)\) CF786B Legacy
有一张 \(n\) 个节点和若干条边。边用 \(q\) 条信息表示:
1 v u w表示有一条连接 \(v \to u\) 的有向边,边权为 \(w\);2 v l r w表示对于所有 \(u \in [l, r]\),都有一条连接 \(v \to u\) 的有向边,边权为 \(w\);3 v l r w表示对于所有 \(u \in [l, r]\),都有一条连接 \(u \to v\) 的有向边,边权为 \(w\)。求 \(s\) 到每个点的最短路。
线段树优化建图。
建两颗线段树“入树”和“出树”,每次连边时将入树的线段树节点连向出树的线段树节点。
同时,在入树中,我们连边儿子 \(\to\) 父亲边权为 \(0\)。在出树中连边父亲 \(\to\) 儿子边权为 \(0\)。
又因为两个数中每个叶子节点本质是一样的,所以在相同的叶子节点间连接边权为 \(0\) 的双向边。
最后从某棵树的叶子节点 \(s\) 跑最短路即可。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1000010;
int n, q, s;
vector<pair<int, int> > g[N];
int root[2];
void add(int a, int b, int w, bool flg = 0) {
g[a].push_back({b, w});
if (flg) add(b, a, w);
return;
}
struct Tree {
int l, r; // 区间
int ls, rs; // 左右儿子
bool flg; // 哪棵树
}tr[N];
int idx;
map<pair<int, bool>, int> Id;
int build(int l, int r, bool flg) {
int u = ++ idx;
tr[u].l = l, tr[u].r = r, tr[u].flg = flg;
if (l != r) {
int mid = l + r >> 1;
tr[u].ls = build(l, mid, flg);
tr[u].rs = build(mid + 1, r, flg);
if (!flg) add(tr[u].ls, u, 0), add(tr[u].rs, u, 0);
else add(u, tr[u].ls, 0), add(u, tr[u].rs, 0);
}
else Id[{l, flg}] = u;
return u;
}
int dis[N];
bool st[N];
void Dijkstra(int s) {
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
q.push({0, s});
memset(dis, 0x3f, sizeof dis);
dis[s] = 0;
while (q.size()) {
int u = q.top().second;
q.pop();
if (st[u]) continue;
st[u] = true;
for (auto t : g[u]) {
int v = t.first, w = t.second;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
return;
}
void u_to_seg(int u, int l, int r, int to, int w) {
if (tr[u].l >= l && tr[u].r <= r) add(to, u, w);
else {
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) u_to_seg(tr[u].ls, l, r, to, w);
if (r > mid) u_to_seg(tr[u].rs, l, r, to, w);
}
return;
}
void seg_to_v(int u, int l, int r, int to, int w) {
if (tr[u].l >= l && tr[u].r <= r) add(u, to, w);
else {
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) seg_to_v(tr[u].ls, l, r, to, w);
if (r > mid) seg_to_v(tr[u].rs, l, r, to, w);
}
return;
}
signed main() {
cin >> n >> q >> s;
root[0] = build(1, n, 0);
root[1] = build(1, n, 1);
for (int i = 1; i <= n; ++ i ) {
add(Id[{i, 0}], Id[{i, 1}], 0, 1);
}
while (q -- ) {
int op, v, u, l, r, w;
cin >> op;
if (op == 1) {
cin >> v >> u >> w;
add(Id[{v, 0}], Id[{u, 1}], w);
}
else if (op == 2) {
cin >> u >> l >> r >> w;
u_to_seg(root[1], l, r, Id[{u, 0}], w);
}
else {
cin >> v >> l >> r >> w;
seg_to_v(root[0], l, r, Id[{v, 1}], w);
}
}
Dijkstra(Id[{s, 0}]);
for (int i = 1; i <= n; ++ i ) {
int res = dis[Id[{i, 0}]];
if (res > 1e15) res = -1;
cout << res << ' ';
}
return 0;
}
\(\color{#9D3DCF}(6)\) P6348 Journeys
有一张 \(n\) 个节点和若干条边。边用 \(m\) 条信息表示:
l1 r1 l2 r2表示对于所有 \(u \in [l1, r1], v \in [l2, r2]\),都有一条双向边连接 \(u, v\)。求 \(P\) 到每个点的最短路。
与上题类似。对于每条信息 l1 r1 l2 r2,我们建立一个虚点,并将 \(l1 \sim r_1\) 和 \(l2 \sim r2\) 向这个虚点连接边权为 \(\frac 12\) 的双向边。这里仍然是线段树优化。
然后跑最短路即可。
实际上,在向虚点连边时可以连接边权为 \(1\) 的边,最终答案全部除以二。
$\color{blue}\text{Code}$
#include <bits/stdc++.h>
using namespace std;
const int N = 5000010;
int n, q, s;
vector<pair<int, double> > g[N];
int root[2];
void add(int a, int b, double w) {
g[a].push_back({b, w});
return;
}
struct Tree {
int l, r; // 区间
int ls, rs; // 左右儿子
bool flg; // 哪棵树
}tr[N];
int idx;
map<pair<int, bool>, int> Id;
int build(int l, int r, bool flg) {
int u = ++ idx;
tr[u].l = l, tr[u].r = r, tr[u].flg = flg;
if (l != r) {
int mid = l + r >> 1;
tr[u].ls = build(l, mid, flg);
tr[u].rs = build(mid + 1, r, flg);
if (!flg) add(tr[u].ls, u, 0), add(tr[u].rs, u, 0);
else add(u, tr[u].ls, 0), add(u, tr[u].rs, 0);
}
else Id[{l, flg}] = u;
return u;
}
double dis[N];
bool st[N];
void Dijkstra(int s) {
priority_queue<pair<double, int>, vector<pair<double, int> >, greater<pair<double, int> > > q;
q.push({0, s});
for (int i = 1; i <= idx; ++ i ) dis[i] = 1e18;
dis[s] = 0;
while (q.size()) {
int u = q.top().second;
q.pop();
if (st[u]) continue;
st[u] = true;
for (auto t : g[u]) {
int v = t.first;
double w = t.second;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v], v});
}
}
}
return;
}
void u_to_seg(int u, int l, int r, int to, double w) {
if (tr[u].l >= l && tr[u].r <= r) add(to, u, w);
else {
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) u_to_seg(tr[u].ls, l, r, to, w);
if (r > mid) u_to_seg(tr[u].rs, l, r, to, w);
}
return;
}
void seg_to_v(int u, int l, int r, int to, double w) {
if (tr[u].l >= l && tr[u].r <= r) add(u, to, w);
else {
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) seg_to_v(tr[u].ls, l, r, to, w);
if (r > mid) seg_to_v(tr[u].rs, l, r, to, w);
}
return;
}
signed main() {
cin >> n >> q >> s;
root[0] = build(1, n, 0);
root[1] = build(1, n, 1);
for (int i = 1; i <= n; ++ i ) {
add(Id[{i, 0}], Id[{i, 1}], 0);
add(Id[{i, 1}], Id[{i, 0}], 0);
}
while (q -- ) {
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
seg_to_v(root[0], l1, r1, ++ idx, 0.5);
u_to_seg(root[1], l2, r2, idx, 0.5);
seg_to_v(root[0], l2, r2, ++ idx, 0.5);
u_to_seg(root[1], l1, r1, idx, 0.5);
}
Dijkstra(Id[{s, 0}]);
for (int i = 1; i <= n; ++ i ) {
cout << dis[Id[{i, 0}]] << '\n';
}
return 0;
}
\((7)\) 区间 chkmax 公差一定的等差数列
- 给定一个整数 \(d\) 和一个初始全为 \(0\) 的长度为 \(n\) 的序列 \(a\)。\(m\) 次修改给定 \(l, r, x\):
- 令序列 \(b_l = x, b_{l+1} = x + d, b_{l+2} = x + 2d, \dots, b_r = x + d(r-l)\)。将所有 \(i \in [l, r]\) 执行 \(a_i \gets \max(a_i, b_i)\)。
- 输出最终的 \(a\)。
发现 \(b\) 就是一个公差为 \(d\) 的等差数列。即操作为:
对于所有 \(i \in [l, r]\) 执行 \(a_i \gets \max(a_i, x + d(i-l))\)。
即:
对于所有 \(i \in [l, r]\) 执行 \(a_i \gets \max(a_i, x - dl + di)\)。
发现只要存在一个覆盖 \(i\) 的操作,它就一定会获得 \(di\) 的贡献。不妨将这个贡献最后计算。每次只操作:
对于所有 \(i \in [l, r]\) 执行 \(a_i \gets \max(a_i, x - dl)\)。
其中 \(x - dl\) 是一个定值。此时就可以用一般线段树维护了。
\(\color{#9D6DCF}(8)\) P4137 Rmq Problem / mex
- 静态区间求 \(\operatorname{mex}\)。
对于区间 \([l, r]\) 而言,根据定义,这个区间的 \(\operatorname{mex}\) 为最小的未出现过的数。
如果 \(\operatorname{mex}_{[l, r]} = x\),那么 \(1 \sim r\) 中 \(x\) 要么没出现过,要么最后一次出现的位置在 \(l\) 之前。
如果固定 \(r\),我们考虑维护值域线段树。现在这颗线段树上的每个节点的值,存储的是 \(1 \sim r\) 中这个值的最后一次出现位置,未出现则为 \(0\)。例如,对于 \(a = \{1, 1, 4, 5, 1, 4\}\),那么这颗线段树就应该是 \(\{5, 0, 0, 6, 4\}\)。
然后对于某个询问 \([l, r]\) 而言,我们需要找到这颗线段树上最靠前的一个值,且这个值 \(< l\)。线段树维护区间最小值并线段树二分即可。
若 \(r\) 不固定,则可将询问离线,按照右端点排序,然后从左往右动态更新这颗值域线段树即可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号