Codeforces Round 925 (Div. 3)

ABC 都是一眼题,用了 16 min。
D 没有一眼看出来,先往后看。E 是博弈论直接跳过。F 一眼出思路。G 一开始都错题了,不会做。遂先写 F。
发现我不会判断图中是否有环。一开始写了个 dfs 以为能过结果复杂度是 \(\mathcal O(n^2)\) 的,罚时 +1。想改成 DP 那样的记忆化发现很假。于是bdfs拓扑排序,写了两个不同的版本,第一个假了,第二个终于过了。 现在已经 67 min 了。
再回来看 D,第二眼会了一个比较麻烦的做法。直接开始写,过时到了 90 min。
然后想做 G。愚蠢的写了个五维 DP \(f_{a, b, c, d, p}\) 表示四种拼图分别由 \(a, b, c, d\) 张,最后一张是 \(p\) 的方案数。但是复杂度是 \(\mathcal O(abcd)\) 的,一开始算成了 \(\mathcal O(a + b + c + d)\)。样例四一直 T,我以为是常数问题,于是在愚蠢地卡常。最后反应过来复杂度不对就放弃了。
E 是博弈论,压根没思路。
A. Recovering a Small String
一个长度为 \(3\) 的由小写字母组成的字符串 \(s\) 的价值被定义为它的每一个字母在字母表中的位置之和。例如 \(\texttt{cat}\) 的价值为 \(3 + 1 + 20 = 24\)。
给定 \(n\),求字典序最小的价值为 \(n\) 的字符串。
多测。\(1 \le t \le 100\),\(3 \le n \le 78\)。
直接枚举 \(s\) 的每一位是哪个字符。我们希望让字典序尽量小,所以我们每一位都 \(\texttt a \sim \texttt z\) 枚举,第一个价值为 \(n\) 的字符串即为答案。
void solve() {
int n = read();
fup (i, 'a', 'z')
fup (j, 'a', 'z')
fup (k, 'a', 'z') {
if (i - 'a' + 1 + j - 'a' + 1 + k - 'a' + 1 == n) {
putchar(i), putchar(j), putchar(k);
puts("");
return;
}
}
}
B. Make Equal
有 \(n\) 个装着水的容器,第 \(i\) 个容器中有 \(a_i\) 单位的水。保证 \(n \mid \sum a_i\)。
你可以进行若干次操作。每次操作你可以从容器 \(i\) 倒入容器 \(j\) 任意数量的水,但是需要满足 \(i < j\)。
问最后能否将所有容器中的水量相同。
多测。\(1 \le t \le 10^4\),\(\sum n \le 2 \times 10^5\),\(0 \le a_i \le 10^9\)。
模拟。
首先求出最终每个容器中的水量,即 \(s = \dfrac 1n\sum a_i\)。
然后从前往后枚举每个容器 \(i\),并记录 \(x\) 表示 \(i\) 之前的容器在留下 \(s\) 单位后剩余的总水量。分类讨论:
- 如果 \(a_i \ge s\):直接将 \(a_i\) 中多余的水倒掉,并将 \(x \gets x + a_i - s\)。
- 如果 \(a_i < s\):首先计算出我需要补充多少水 \(y = s - a_i\),那么:
- 如果 \(y \le x\):直接将前面剩下的水倒入容器 \(i\) 中,并将 \(x \gets x - y\);
- 如果 \(y > x\):答案为 NO,结束即可。
最后如果都能填完输出 YES。
void solve() {
int n = read(), s = 0;
vector<int> a(n);
for (int &t : a) t = read(), s += t;
s /= n;
int x = 0;
for (int &t : a) {
if (t >= s) x += t - s;
else {
int y = s - t;
if (y > x) return puts("NO"), void();
x -= y;
}
}
puts("YES");
}
C. Make Equal Again
给定一个长度为 \(n\) 的数组 \(a\)。
你可以进行至多一次操作。你可以选择三个整数 \(i, j, x(1 \le i \le j \le n)\) 并将 \(a_i \sim a_j\) 都替换为 \(x\),代价为 \(j - i + 1\)。
求如果要将 \(a\) 数组中的所有元素变得相同的最小代价。
多测。\(1 \le t \le 10^4\),\(\sum n \le 2 \times 10^5\),\(1 \le a_i \le n\)。
首先分别算出从头和从尾最多有多少元素保持相同。即计算最大的 \(x, y\) 使得 \(a_x = a_{x - 1} = \dots = a_1\),\(a_{n - y + 1} = a_{n - y +2} = \dots = a_n\)。
如果 \(a_1 \ne a_n\),则答案为 \(\min(n - x, n - y)\)。否则答案为 \(n - x - y\)。
但是需要先特判是否最初 \(a\) 中的元素相同。若是输出 \(0\)。
int solve() {
int n = read();
vector<int> a(n);
for (int &t : a) t = read();
if (*max_element(a.begin(), a.end()) == *min_element(a.begin(), a.end())) return 0;
int res, x, y;
fup (i, 1, n - 1) {
if (a[i] != a[i - 1]) {
x = i;
break;
}
}
fdw (i, n - 2, 0) {
if (a[i] != a[i + 1]) {
y = n - 1 - i;
break;
}
}
res = min(n - x, n - y);
if (a[0] == a[n - 1]) {
res = n - x - y;
}
return res;
}
D. Divisible Pairs
给定一个长度为 \(n\) 的数组 \(a\) 和两个整数 \(x, y\)。
你需要找有多少数对 \(i, j(1 \le i < j \le n)\) 满足 \(x \mid (a_i + a_j)\) 且 \(y \mid (a_i - a_j)\)。
多测。\(1 \le t \le 10^4\),\(\sum n \le 2 \times 10^5\),\(1 \le x, y, a_i \le 10^9\)。
首先处理第二个条件 \(y \mid (a_i - a_j)\)。不难发现如果这个条件满足就意味着 \(a_i \equiv a_j \pmod y\)。
所以我们可以用 map + vector 存储每个除以 \(y\) 的余数出现的位置。
map<int, vector<int> > v;
for (int i = 1; i <= n; ++ i ) {
scanf("%d", a + i);
v[a[i] % y].push_back(i);
}
然后我们需要在每个 vector 中找整数 \(i, j(i < j)\) 使得 \((a_i + a_j) \bmod x = 0\),即 \(a_i \bmod x + a_j \bmod x \equiv 0 \pmod x\)。
这仍然启发我们用 map 维护一个桶,表示对于每一个除以 \(x\) 的余数出现了多少次。
然后我们枚举上述 \(i\),那么 \(j\) 的个数即满足 \(a_i + a_j \equiv 0 \pmod x\) 的 \(j\) 的个数,即满足 \(a_j \equiv x - a_i \pmod x\) 的 \(j\) 的个数。然后用最开始维护的桶计算即可。
注意这样计算我们并没有满足 \(i < j\) 这个条件,但是不难发现我们算出的答案是最终答案的两倍。
最终时间复杂度相当于是每个 vector 的大小之和,即 \(n\)。加上 STL 总时间复杂度为 \(\mathcal O(n \log n)\)。
int T, n, a[N], x, y;
map<int, vector<int> > v;
map<int, int> p;
LL solve() {
scanf("%d%d%d", &n, &x, &y);
v.clear();
for (int i = 1; i <= n; ++ i ) {
scanf("%d", a + i);
v[a[i] % y].push_back(i);
}
LL res = 0;
for (auto t : v) {
int i = t.fi;
p.clear();
for (int &l : t.se) {
++ p[a[l] % x];
}
for (auto o : p) {
int l = o.fi;
int r = l ? x - l : 0;
if (l == r) res += (LL)p[l] * (p[l] - 1); // 注意判断相同的情况
else res += (LL)p[l] * p[r];
}
}
return res / 2;
}
E. Anna and the Valentine's Day Gift
Anna 和 Sasha 在玩游戏,他们有一个长度为 \(n\) 的数组 \(a\)。
Anna 为先手。两人分别操作:
- 轮到 Anna 时,她首先需要选择一个 \(a_i\),并将其按照数位翻转,并省略前导零。例如 \(42\) 翻转为 \(24\),\(1580\) 翻转为 \(851\)。这样操作后,\(a\) 数组大小不变。
- 轮到 Sasha 时,他需要选择 \(a_i, a_j(i \ne j)\),并以任意顺序将其连接。例如 \(2007\) 和 \(19\) 可以连接为 \(200719\) 或 \(192007\)。这样操作后,\(a\) 数组大小减一。
玩家不能跳过回合。当 \(a\) 中只剩下一个整数时,如果它大于等于 \(10^m\),Sasha 获胜。否则 Anna 获胜。
如果 Anna 和 Sasha 都以最优方式操作,谁会获胜?
多测。\(1 \le t \le 10^4\),\(\sum n \le 2 \times 10^5\),\(0 \le m \le 2 \times 10^9\)。
F. Chat Screenshots
有 \(n\) 个人在排队,编号 \(1 \sim n\)。他们已经按照一定的顺序排好队了。
其中的 \(k\) 个人发了 \(k\) 条消息,表示他看到的所有人的排队顺序。但是每个人发的消息中都把自己放在了最前面。
请你判断这 \(k\) 个人是否都说的是真话。
多测。\(1 \le t \le 10^4\),\(1 \le k \le n \le 2 \times 10^5\),\(\sum n\cdot k \le 2 \times 10^5\)。
由于每条消息的发送者都会把自己排在最前面,所以所有的 \(a_{i, 1}\) 都是没有用的。我们推理需要用的信息为 \(a_{i, 2}, a_{i, 3}, \dots, a_{i, n}\)。
这些信息意味着 \(a_{i, 2}\) 一定在 \(a_{i, 3}\) 之前,\(a_{i, 3}\) 一定在 \(a_{i, 4}\) 之前,以此类推,\(a_{i, k - 1}\) 一定在 \(a_{i, k}\) 之前。
对于这种两者之间有关系的推理,可以启发我们将其转化成图论问题。
若我们将 \(a_{i, j} \to a_{i, j + 1}(2 \le j < k)\) 连边,表示 \(a_{i, j}\) 在 \(a_{i, j + 1}\) 之前。那么如果最终的图中有环,就代表答案为 NO。反之为 YES。
判断图中是否有环可以使用拓扑排序。若我们用拓扑排序的方法遍历完整张图后,存在节点没有遍历到,那么图中有环。否则无环。
void solve() {
scanf("%d%d", &n, &k);
for (int i = 1; i <= k; ++ i ) {
int x, y;
scanf("%d", &x);
for (int j = 2; j <= n; ++ j ) {
scanf("%d", &y);
if (j != 2) g[x].push_back(y);
x = y;
}
}
for (int i = 1; i <= n; ++ i ) {
sort(g[i].begin(), g[i].end());
g[i].erase(unique(g[i].begin(), g[i].end()), g[i].end());
for (int j : g[i]) ++ d[j];
}
int cnt = 0;
queue<int> q;
for (int i = 1; i <= n; ++ i )
if (!d[i])
q.push(i),
st[i] = true;
while (q.size()) {
int t = q.front();
q.pop();
for (int v : g[t]) {
if (!st[v]) {
if (!( -- d[v])) {
st[v] = true;
q.push(v);
}
}
}
}
for (int i = 1; i <= n; ++ i ) cnt += st[i];
puts(cnt == n ? "Yes" : "No");
}
G. One-Dimensional Puzzle
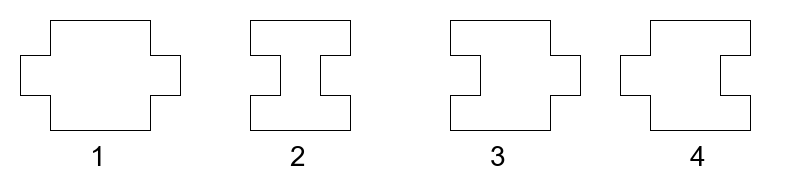
有 \(4\) 种拼图,其中第 \(i\) 种拼图有 \(c_i\) 张。
两张拼图可以连结当且仅当它们相邻的卡槽中一个凹陷一个突出。
我们希望将所有的拼图从左往右拼起来,求总方案数。答案对 \(998244353\) 取模。
多测。\(1 \le t \le 2 \times 10^5\),\(0 \le c_i \le 10^6\),\(\sum (c_1+c_2+c_3+c_4) \le 4 \times 10^6\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号