AtCoder Beginner Contest 339
AtCoder Beginner Contest 339
最水的一场，但打得稀里哗啦。
E - Smooth Subsequence
Problem Statement
You are given a sequence \(A = (A_1, A_2, \ldots, A_N)\) of length \(N\).
Find the maximum length of a subsequence of \(A\) such that the absolute difference between any two adjacent terms is at most \(D\).
A subsequence of a sequence \(A\) is a sequence that can be obtained by deleting zero or more elements from \(A\) and arranging the remaining elements in their original order.
Constraints
- \(1 \leq N \leq 5 \times 10^5\)
- \(0 \leq D \leq 5 \times 10^5\)
- \(1 \leq A_i \leq 5 \times 10^5\)
- All input values are integers.
Solution
一眼 DP。
设 \(f_i\) 表示以 \(a_i\) 结尾的最长子序列的长度。转移需要枚举子序列倒数第二个元素 \(a_j\)，需要保证 \(|a_i - a_j| \le D\) 且 \(j < i\)。方程为：
然后可以发现如果要满足 \(|a_i - a_j| \le D\)，那么一定有 \(a_i - D \le a_j \le a_i + D\)。所以可以直接以 \(a\) 数值做下标维护权值线段树 \(g\)。那么：
所以写单点修改区间查询的线段树就结束了。
Code
int n, d, a[N];
int f[N];
struct Tree {
int l, r, v;
}tr[N << 2];
void pushup(int u) {
tr[u].v = max(tr[ls].v, tr[rs].v);
return;
}
void build(int u, int l, int r) {
tr[u] = {l, r};
if (l != r) {
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
}
return;
}
void modify(int u, int x, int d) {
if (tr[u].l == tr[u].r) tr[u].v = max(tr[u].v, d);
else {
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(ls, x, d);
else modify(rs, x, d);
pushup(u);
}
return;
}
int query(int u, int l, int r) {
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = 0;
if (l <= mid) res = query(ls, l, r);
if (r > mid) res = max(res, query(rs, l, r));
return res;
}
signed main()
{
n = read(), d = read();
read(a + 1, a + n + 1);
build(1, 1, 5e5);
int res = 0;
fup (i, 1, n) {
f[i] = max(1ll, query(1, max(1ll, a[i] - d), min(500000ll, a[i] + d)) + 1);
modify(1, a[i], f[i]);
res = max(f[i], res);
}
wel(res);
return 0;
}
F - Product Equality
Problem Statement
You are given \(N\) integers \(A_1, A_2, \dots, A_N\).
Find the number of triples of integers \((i, j, k)\) that satisfy the following conditions:
- \(1 \le i, j, k \le N\)
- \(A_i \times A_j = A_k\)
Constraints
- \(1 \le N \le 1000\)
- \(\color{red}{1 \le A_i < 10^{1000}}\)
Solution
如果 \(a \times b = c\)，那么显然有 \(((a \bmod p) \times (b \bmod p)) \bmod p = c \bmod p\)。
反过来，如果 \(((a \bmod p) \times (b \bmod p)) \bmod p = c \bmod p\)，那么有概率 \(a \times b = c\)。
当这个 \(p\) 是个大质数时，这个成功的概率就很大。
这启发我们将读入的 \(A_i\) 对一个大质数 \(p\) 取模，然后枚举两个数，map 计算第三个数的可能性，累计答案即可。
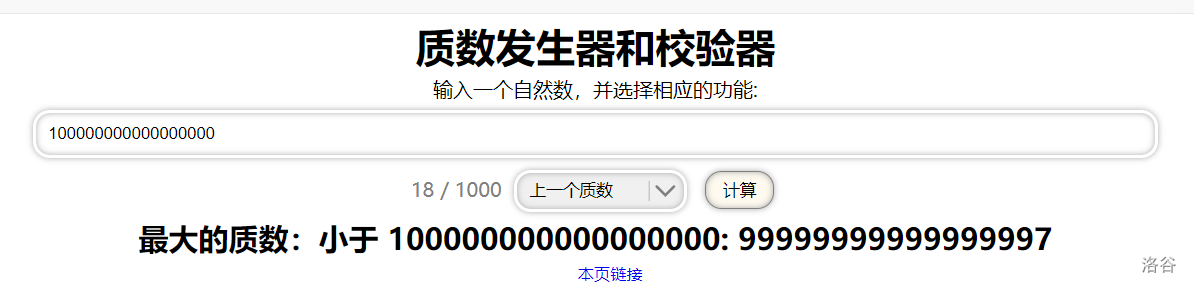
找一个大质数可以这样做：
- 打开一个叫作质数发生器和校验器的东西；
- 选择“上一个质数”；
- 上面的框里输上 \(100000000000000000\)（\(10^{17}\)），点击计算。
Code
注意要开 __int128。
#define int __int128
const int P = 99999999999999997;
int n, a[N];
map<int, int> p;
signed main()
{
n = read();
fup (i, 1, n) {
string s;
cin >> s;
for (char &t : s) a[i] = (a[i] * 10 + t - '0') % P;
++ p[a[i]];
}
int res = 0;
fup (i, 1, n)
fup (j, 1, n)
res += p[a[i] * a[j] % P];
wel(res);
return 0;
}
G - Smaller Sum
Problem Statement
You are given a sequence \(A=(A_1,A_2,\dots,A_N)\) of length \(N\).
Answer the following \(Q\) queries. The \(i\)-th query is as follows:
- Find the sum of the elements among \(A_{L_i},A_{L_i+1},\dots,A_{R_i}\) that are not greater than \(X_i\).
Here, you need to answer these queries online.
That is, only after you answer the current query is the next query revealed.
For this reason, instead of the \(i\)-th query itself, you are given encrypted inputs \(\alpha_i, \beta_i, \gamma_i\) for the query. Restore the original \(i\)-th query using the following steps and then answer it.
- Let \(B_0=0\) and \(B_i =\) (the answer to the \(i\)-th query).
- Then, the query can be decrypted as follows:
- \(L_i = \alpha_i \oplus B_{i-1}\)
- \(R_i = \beta_i \oplus B_{i-1}\)
- \(X_i = \gamma_i \oplus B_{i-1}\)
Here, \(x \oplus y\) denotes the bitwise XOR of \(x\) and \(y\).
What is bitwise XOR? The bitwise XOR of non-negative integers \(A\) and \(B\), \(A \oplus B\), is defined as follows:
- The digit in the \(2^k\) place (\(k \geq 0\)) of \(A \oplus B\) in binary is \(1\) if exactly one of the corresponding digits of \(A\) and \(B\) in binary is \(1\), and \(0\) otherwise.
For example, \(3 \oplus 5 = 6\) (in binary: \(011 \oplus 101 = 110\)).
Constraints
- All input values are integers.
- \(1 \le N \le 2 \times 10^5\)
- \(0 \le A_i \le 10^9\)
- \(1 \le Q \le 2 \times 10^5\)
- For the encrypted inputs, the following holds:
- \(0 \le \alpha_i, \beta_i, \gamma_i \le 10^{18}\)
- For the decrypted queries, the following holds:
- \(1 \le L_i \le R_i \le N\)
- \(0 \le X_i \le 10^9\)
Solution
某大神曾经说过：“看到一道 ABC G 题，我们第一想到的应该是卡常和分块”。
做法分块。
维护每个块的左右端点，并在最开始将块内元素排序。
查询时，对于在边上的两个块，我们暴力处理。注意这里需要处理最开始的原序列。
对于中间的块，由于已经排好序了，所以可以直接二分找到最后一个满足它的值小于等于 \(x\) 的位置。那么在这之前的元素都是满足要求的。
注意块长需要调成 \(\sqrt{n \log n}\)，然后就是基础卡常了。总时间复杂度差不多 \(\Theta(n \log n + q \sqrt n \log n)\)。
Code
int n, q, a[N], b[N];
LL l, r, k;
LL s[N]; // 前缀和
struct Node {
int l, r;
}p[N];
int t[N], cnt, B;
inline void build() {
register int l = 1, r = B;
while (r <= n) {
p[ ++ cnt] = {l, r};
fup (i, l, r) t[i] = cnt;
sort(a + l, a + r + 1);
l += B, r += B;
}
if (r != n) {
r = n;
p[ ++ cnt] = {l, r};
fup (i, l, r) t[i] = cnt;
sort(a + l, a + r + 1);
}
fup (i, 1, n) s[i] = s[i - 1] + a[i];
return;
}
inline LL query(const int& l, const int& r, const LL& k) {
const int& L = t[l], R = t[r];
register LL res = 0;
if (L == R) {
fup (i, l, r) res += (b[i] <= k) * b[i];
return res;
}
fup (i, l, p[L].r) res += (b[i] <= k) * b[i];
fup (i, p[R].l, r) res += (b[i] <= k) * b[i];
fup (i, L + 1, R - 1) {
register int x = p[i].l, y = p[i].r, pos = p[i].l - 1;
while (x <= y) {
const int& mid = x + y >> 1;
if (a[mid] <= k) pos = mid, x = mid + 1;
else y = mid - 1;
}
res += s[pos] - s[p[i].l - 1];
}
return res;
}
signed main()
{
n = read();
B = sqrt(n * log2(n));
fup (i, 1, n) a[i] = b[i] = read();
build();
q = read();
register LL lst = 0;
while (q -- ) {
l = (read() ^ lst), r = (read() ^ lst), k = (read() ^ lst);
lst = query(l, r, k);
wel(lst);
}
return 0;
}
