AtCoder Beginner Contest 336
AtCoder Beginner Contest 336

57 秒切 A,75 秒切 B。
然后 C 就卡了,没想到五进制,二分答案加数位 DP 判断过了。用了半个小时。
DE 读完题,发现 D 可做。小推了一下发现可以维护线段树。
很快写完过了样例。
第一发罚时,\(+1\) 和 \(-1\) 写反了。
第二发罚时,把那个“金字塔”写成了 \((1, 2, \dots k, 1, 2, \dots, k - 1)\) 的形式。
第三发,第四发,第五发,第六发,第七发都是有四个或三个点没过。
第八发过了。原因竟是线段树 query 没 pushdown。
D 是在结束前三分钟切的。E 当然就没时间了。
C - Even Digits
想复杂了。
Description
A non-negative integer \(n\) is called a good integer when it satisfies the following condition:
- All digits in the decimal notation of \(n\) are even numbers (\(0\), \(2\), \(4\), \(6\), and \(8\)).
For example, \(0\), \(68\), and \(2024\) are good integers.
You are given an integer \(N\). Find the \(N\)-th smallest good integer.
Solution1 二分 + 数位 DP
二分 \(mid\),然后求 \(0 \sim mid\) 中有多少个好整数。
发现这个形式很像数位 DP。于是套路的将 \(mid\) 十进制拆分然后计算。
具体的是代码。
Solution2 五进制
我们可以将 \(n\) 转化成五进制。例如 \((7)_{10} = (12)_5\)。将这个五进制数看作是十进制数,然后将每一位乘 \(2\)。
注意题目中 \(0\) 也算好整数,所以 \(n\) 应当减一。所以上面说的实际上是 \(n = 8\) 的情况。
时间复杂度 \(\mathcal O(\log_5n)\)。代码。
D - Pyramid
仍然想复杂了。
Description
For a positive integer \(k\), the Pyramid Sequence of size \(k\) is a sequence of length \((2k-1)\) where the terms of the sequence have the values \(1,2,\ldots,k-1,k,k-1,\ldots,2,1\) in this order.
You are given a sequence \(A=(A_1,A_2,\ldots,A_N)\) of length \(N\).
Find the maximum size of a Pyramid Sequence that can be obtained by repeatedly choosing and performing one of the following operations on \(A\) (possibly zero times).
- Choose one term of the sequence and decrease its value by \(1\).
- Remove the first or last term.
It can be proved that the constraints of the problem guarantee that at least one Pyramid Sequence can be obtained by repeating the operations.
Solution1 二分 + 线段树
发现答案是有单调性的(如果 \(k\) 满足,那么比 \(k\) 小的数也能满足),因此二分这个 \(k\)。
接下来的问题就是在 \(a\) 中找到一个长度为 \(2k - 1\) 子区间 \([l, r]\),使得每一个 \(a_i\) 都大于等于它应该变成的数。这里应该变成的数就是题目中的金字塔数。
我们令 \(c_i\) 表示 \(a_i\) 减去它应该变到的数。那么如果这个区间 \([l, r]\) 是满足条件的,就意味着每个 \(l \le i \le r\) 都有 \(c_i \ge 0\)。也就是:
所以在二分 check 的时候可以计算出这个 \(c\) 数组来,然后判断上述条件是否满足。
但是对于每个区间 \([l, r]\) 都暴力计算 \(c\) 时不优的,需要优化它。看这个例子:
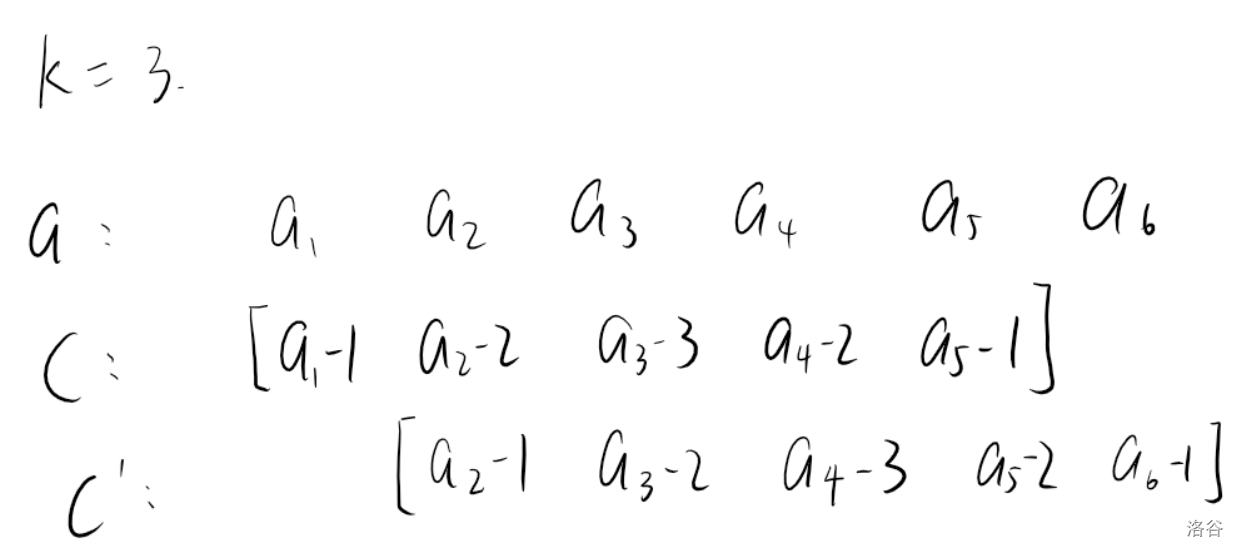
可以发现,在这个变化过程中。\(c_1 \sim c_3\) 的值都增加了 \(1\),\(c_4 \sim c_6\) 的值都减少了 \(1\)。
具体地,当从区间 \([l, r]\) 变成区间 \([l+1, r+1]\) 时:
- 对于所有 \(l \le i \le l + k - 1\),\(c_i \gets c_i + 1\);
- 对于所有 \(l + k \le i \le r + 1\),\(c_i \gets c_i - 1\)。
然后发现 \(c\) 用到了区间加和求最小值。lazy_tag 的线段树即可。
时间复杂度 \(\mathcal O(n \log^2n)\)。
具体看代码。
Solution2 递推
令 \(pre_i\) 表示如果以 \(i\) 为金字塔的中点,那么从 \(i\) 开始,最多能往左扩展多少。
令 \(suf_i\) 表示如果以 \(i\) 为金字塔的中点,那么从 \(i\) 开始,最多能往右扩展多少。
有递推:
- \(pre_i = \min(a_i, pre_{i - 1} + 1)\);
- \(suf_i = \min(a_i, suf_{i + 1} + 1)\)。
那么答案为 \(\max_{i = 1}^n \min(pre_i, suf_i)\)。
原因显然。时间复杂度 \(\mathcal O(n)\)。
代码。
E - Digit Sum Divisible
跟 @xz001 学会了记忆化搜索的数位 DP。
Description
The digit sum of a positive integer \(n\) is defined as the sum of the digits in the decimal notation of \(n\). For example, the digit sum of \(2024\) is \(2+0+2+4=8\).
A positive integer \(n\) is called a good integer when \(n\) is divisible by its digit sum. For example, \(2024\) is a good integer because it is divisible by its digit sum of \(8\).
You are given a positive integer \(N\). How many good integers are less than or equal to \(N\)?
Solution
数位 DP。
可以发现数位和最大为 \(9 \times 14 = 126\)(每一位都填 \(9\),填 \(14\) 位)。因此我们先枚举数位和 \(m\)。
设状态 \(f_{i, j, k, l}\),其中:
- \(i\):搜到了第 \(i\) 位(倒着枚举,也就是指 \(i\) 到最高位都填完了)。
- \(j\):是否 \(i\) 前面的位(包括 \(i\))都填满了。这里的填满指填的与原数 \(n\) 相同。例如 \(114514\) 就是在 \(n = 119198\) 时第五到最高位的填满。
- \(k\):\(i\) 前面的位从左往右拼成的十进制数模数位和为 \(k\)。例如 \(114514\) 的第四到最后一位组成的十进制数为 \(114\)。
- \(l\):\(i\) 前面的数位和为 \(l\)。例如 \(114514\) 的第四到最后一位的数位和为 \(11\)。
转移是这样的:
- \(f_{i, 0, k, l} = \sum\limits_{t = 0}^9 f_{i - 1, 0, (10k + t) \bmod m, l + t}\)。表示枚举第 \(i\) 位填的数为 \(t\)。那么因为前面存在某一位没填满,那么后面的位 \(0 \sim 9\) 都是可以填的。因此 \(t\) 的范围为 \([0, 9]\)。
- \(f_{i, 1, k, l} = \sum\limits_{t = 0}^pf_{i - 1, [t = p],(10k + t) \bmod m, l + t}\),其中 \(p\) 表示给定的 \(n\) 的第 \(i\) 位,\([t = p]\) 表示 \(t\) 是否等于 \(p\)(真为 \(1\),假为 \(0\))。表示枚举的第 \(i\) 位为 \(t\)。那么因为前面每一位都填满了,那么这一位肯定不能超过 \(n\) 原来的这一位,所以枚举到 \(p\)。
令 \(c\) 表示 \(n\) 的位数。那么答案为 \(f_{c, 1, 0, 0}\)。
边界显然 \(f_{0, 0, 0, m} = f_{0, 1, 0, m} = 1\),其余 \(i = 0\) 的 \(f_{i, j, k, l} = 0\)。
代码。
F - Rotation Puzzle
水题。赛时没看。
Description
Problem Statement
There is a grid with \(H\) rows and \(W\) columns. Initially, each integer from \(1\) to \((H \times W)\) is written exactly once in the grid.
Specifically, for \(1 \leq i \leq H\) and \(1 \leq j \leq W\), the cell at the \(i\)-th row from the top and the \(j\)-th column from the left contains \(S_{i,j}\).
Below, let \((i,j)\) denote the cell at the \(i\)-th row from the top and the \(j\)-th column from the left.
Determine if it is possible to reach a state where, for all pairs of integers \((i,j)\) \((1 \leq i \leq H, 1 \leq j \leq W)\),
the cell \((i,j)\) contains the integer \(((i-1) \times W + j)\) by repeating the following operation at most \(20\) times (possibly zero).
If it is possible, print the minimum number of operations required.
If it is impossible in \(20\) or fewer operations (including the case where it is impossible no matter how many times the operation is repeated), print \(-1\).
Operation: Choose a rectangle of size \((H-1) \times (W-1)\) from the grid and rotate it \(180\) degrees.
More precisely, choose integers \(x\) and \(y\) \((0 \leq x, y \leq 1)\),
and for all pairs of integers \((i,j)\) satisfying \(1 \leq i \leq H-1\) and \(1 \leq j \leq W-1\),
simultaneously replace the integer written in cell \((i+x,j+y)\) with the number written in cell \((H-i+x,W-j+y)\).
Note that it is only necessary for the integers written in the cells to satisfy the condition; the orientation in which they are written does not matter.
- \(3 \leq H,W \leq 8\)
- \(1 \leq S_{i,j} \leq H \times W\)
- If \((i,j) \neq (i',j')\), then \(S_{i,j} \neq S_{i',j'}\)
- All input values are integers.
Solution
可以发现,对于每种状态,它会有 \(4\) 种可以变成的状态。也就是说暴力枚举的复杂度约 \(4^{20}\)。显然是不行的。
但是发现这个旋转 \(180 ^\circ\) 操作就很像是可以双向搜索的形式。我们令读入的矩阵为 \(A\),目标矩阵(也就是 \(1, 2, 3, \dots\))为 \(B\)。那么我们从 \(A, B\) 各开始搜索 \(10\) 步,然后在搜索空间中取交集,然后求变化次数的最小值即可。
复杂度约为 \(2 \times 4^{10}\)。
思路不难,实现略需技巧。代码。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号