关于 LIS，它没死，
0. 前言
LIS（最长上升子序列）为 DP（动态规划）的经典题型，也经常最为初学者们最先接触的 DP 题目。本文将详细介绍有关 LIS 的内容及拓展。
让我们从这一个简单问题开始：
给定一个长度为 \(n\) 的序列 \(a\)，请你求出它的最长上升子序列长度。
1. 最初的 DP
我们设 \(f_i\) 表示序列 \(a_{1 \sim i}\) 的最长上升子序列，那么显然答案为 \(f_n\)。这样设立状态发现并不好转移，于是我们给状态增加一个限制，即必须以 \(a_i\) 结尾。那么 \(f_i\) 就表示在 \(a_{1 \sim i}\) 中最长的且以 \(a_i\) 结尾的上升子序列的长度。
对于转移，我们可以找到最后一个不同的地方。由于最后一个元素一定是以 \(i\) 结尾的，所以我们可以枚举倒数第二个元素的位置 \(j\)，很显然这需要满足 \(1 \le j < i\) 而且 \(a_j < a_i\)。然后答案就是以 \(a_j\) 结尾的最长上升子序列长度加 \(1\)，即：
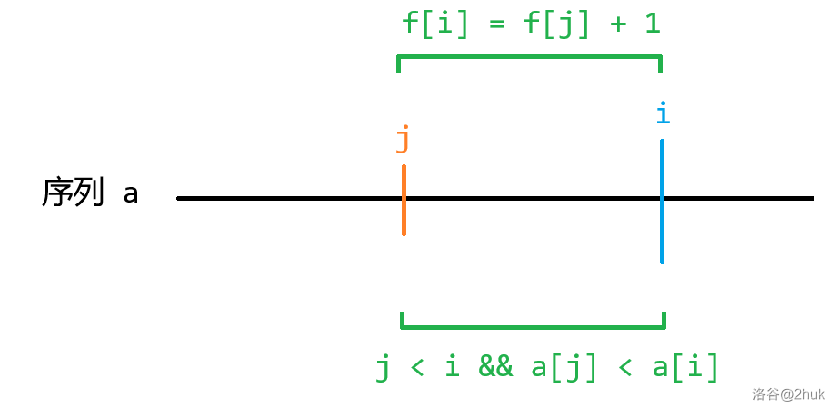
答案显然为 \(\max_{1 \le i \le n}(f_i)\)。
for (int i = 1; i <= n; ++ i )
{
f[i] = 1; // 因为 1 个元素也是上升子序列
for (int j = 1; j < i; ++ j )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
时间复杂度 \(\Theta(n^2)\)。
2. 优化
2.1. 贪心 + 二分
对于 \([1, 4, 2, 3]\) 这个序列，首先我们知道 \([1, 4]\) 和 \([1, 2]\) 都是长度为 \(2\) 的上升子序列，那么如果此时如果需要保存一个下来，我们留取哪个比较好呢？
不难看出应当留下 \([1, 2]\) 这个子序列。因为留下它后最后一个 \(3\) 就可以接到 \([1, 2]\) 后面，获得一个全新的上升子序列 \([1, 2, 3]\) 而获得更优的答案。
一般化这个问题。若有多个相同长度的上升子序列，那么我们只需要留下最后一个元素最小的子序列即可。
这是思路。考虑实现这个想法。
我们定义 \(q_i\) 表示长度为 \(i\) 的所有上升子序列中，最后一个元素的最小值。那么在枚举到某一个元素 \(a_x\) 时，首先我们需要找到所有当前结尾元素仍然小于 \(a_x\) 的上升子序列，然后找一个长度最长的并将 \(a_x\) 插在它的后面。若找到的最长子序列的长度为 \(k\)，那么将 \(a_x\) 插在这个子序列后长度就变为了 \(k + 1\)。
如果仍然暴力去寻找这个子序列，复杂度仍为 \(\Theta(n^2)\)。但是我们可以观察一个性质，就是上升子序列越长，最后一个元素的最小值一定不会越小。也就是说 \(\bm{q_i}\) 一定单调递增。
这启发我们可以二分查找这个合法的上升子序列。具体的，我们要二分找到最后一个（因为越靠后下标越大，即上升子序列长度越大）小于 \(a_x\) 的 \(q_k\)，并将 \(a_x\) 插入它所代表的上升子序列的结尾。这一步是虚拟的，我们要做的就是将 \(q_{k + 1}\) 的值修改为 \(a_x\)。
最后的答案就是 \(q\) 数组的长度。
int len = 0;
for (int i = 1; i <= n; ++ i )
{
int l = 1, r = len, pos = 0;
while (l <= r)
{
int mid = l + r >> 1;
if (q[mid] < a[i]) pos = mid, l = mid + 1;
else r = mid - 1;
}
q[pos + 1] = a[i];
if (pos == len) ++ len;
}
cout << len;
2.2. 树状数组
如果我们将权值作为下标，那么对于一个元素 \(a_i\)，我们只需要在下标在 \([1, a_i)\) 范围内找一个最大值。因为我们从前往后（即 \(i\) 从小到大）计算，所以在此时计算 \(a_i\) 时所有已经被计算过的 \(a_j\) 一定满足 \(j < i\)，这样就满足了 \(j < i\) 且 \(a_j < a_i\) 这两个条件。
计算完后，我们在下标为 \(a_i\) 的位置上更新答案，最后在所有答案中找最大值即可。
上述操作用到了“求前缀最大值”和“单点修改”，因此树状数组维护即可。
注意由于 \(a_i\) 可能很大，所以可以考虑离散化或者用 map 维护树状数组。下面是用的离散化。
void modify(int u, int k)
{
for (int i = u; i <= n; i += lowbit(i))
tr[i] = max(tr[i], k);
}
int query(int u)
{
int res = 0;
for (int i = u; i; i -= lowbit(i))
res = max(res, tr[i]);
return res;
}
cin >> n;
for (int i = 1; i <= n; ++ i ) cin >> a[i], b[i] = a[i];
sort(b + 1, b + n + 1);
int len = unique(b + 1, b + n + 1) - b - 1;
for (int i = 1; i <= n; ++ i )
{
int k = lower_bound(b + 1, b + len + 1, a[i]) - b;
int q = query(k - 1) + 1;
modify(k, q);
res = max(res, q);
}
cout << res;
3. 例题
3.1
给定一个长度为 \(n\) 的序列，其中第 \(i\) 个元素有两个属性 \(a_i, b_i\)。请你从中选择一个子序列，使得 \(a_i\) 递增。求最大的子序列的 \(b\) 属性之和。
\(1 \le a_i \le n \le 2 \times 10^5\)，\(1 \le b_i \le 10^9\)。
设状态 \(f_i\) 表示考虑前 \(i\) 个元素，且第 \(i\) 个元素一定选的最大答案。则方程显然：
答案为 \(\max_{i = 1}^n(f_i)\)。直接这样做复杂度是 \(\Theta (n^2)\) 的。考虑优化。
首先注意到，\(a_i\) 一定是小于等于 \(n\) 的。那么我们可以将 \(a\) 值作下标，那么在求 \(a_j < a_i\) 时只需要枚举下标 \([1, a_i)\) 即可。
具体的，我们定义 \(g_i\) 为当前节点的 \(a\) 属性为 \(i\) 时的答案，则转移方程如下：
此时可以发现，上面的 \(g\) 数组用到了“前缀求最大值”和“单点修改”，因此树状数组维护即可。
时间复杂度 \(\Theta (n \log n)\)。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 200010;
int n, a[N], b[N], f[N];
int tr[N];
int lowbit(int x)
{
return x & -x;
}
void modify(int u, int x)
{
for (int i = u; i <= n; i += lowbit(i))
tr[i] = max(tr[i], x);
}
int query(int u)
{
int res = 0;
for (int i = u; i; i -= lowbit(i))
res = max(res, tr[i]);
return res;
}
main()
{
cin >> n;
for (int i = 1; i <= n; ++ i ) cin >> a[i];
for (int i = 1; i <= n; ++ i ) cin >> b[i];
for (int i = 1; i <= n; ++ i )
{
f[i] = query(a[i] - 1) + b[i];
modify(a[i], f[i]);
}
cout << *max_element(f + 1, f + n + 1);
return 0;
}
3.2
简化题意：有上下两条直线，每条直线上有 \(n\) 个点。已知有 \(n\) 条线段，第 \(i\) 条线段连接第一条直线的 \(x_i\) 和第二条直线的 \(y_i\)。请你选出一些线段，使得两两之间没有交叉。求最多的选择的线段数。
\(1 \le n \le 2 \times 10^5\)。
考虑这样实现：首先我们将每条线段按 \(x_i\) 升序排序，那么 \(y_i\) 就成为了一些杂乱无序的点。此时，我们需要选择一些 \(y_i\)，使得 \(y_i\) 单调上升，那么选择的 \(y_i\) 的数量就是答案。
例如下图：
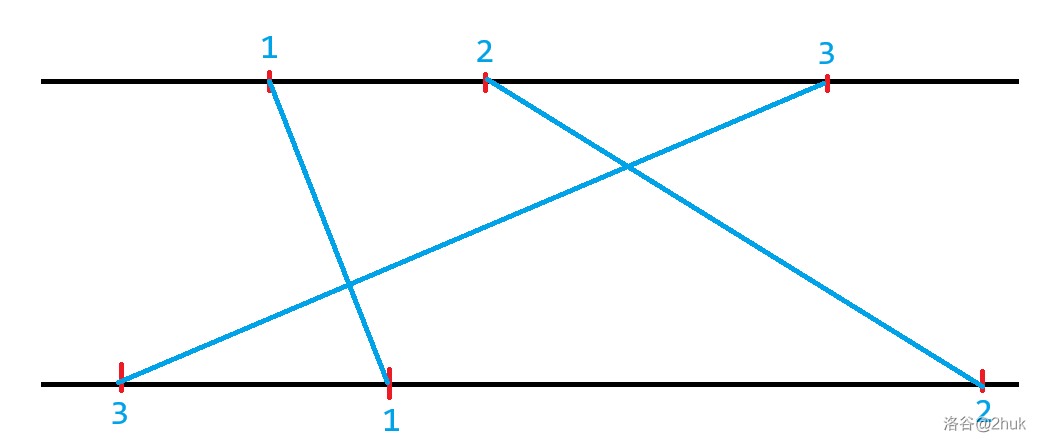
*其中蓝字 \(1, 2, 3\) 表示线段编号，已按 \(x_i\) 从小到大排序。
那么我们显然不能选择 \(1, 3\) 线段，因为 \(3\) 线段的 \(x_i\) 大于 \(1\) 线段的 \(x_i\)，但 \(3\) 线段的 \(y_i\) 小于 \(1\) 线段的 \(y_i\)，导致了交叉。
避免这种情况就是需要找到随着 \(x_i\) 递增 \(y_i\) 也递增的线段。因为我们将 \(x_i\) 排序了，所以问题等价于需要找到随着 \(i\) 递增 \(y_i\) 也递增的线段。那么答案即为 \(y_i\) 的最长上升子序列长度。
时间复杂度 \(\Theta (n \log n)\)。
#include <iostream>
#include <algorithm>
const int N = 2e5 + 10;
using namespace std;
int n, res, q[N], len;
pair<int, int> a[N];
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i )
cin >> a[i].first >> a[i].second;
sort(a + 1, a + n + 1);
int len = 0;
for (int i = 1; i <= n; ++ i )
{
int l = 1, r = len, pos = 0;
while (l <= r)
{
int mid = l + r >> 1;
if (q[mid] < a[i].second) pos = mid, l = mid + 1;
else r = mid - 1;
}
q[pos + 1] = a[i].second;
if (pos == len) ++ len;
}
cout << len;
return 0;
}
3.3
给定 \(1,2,\ldots,n\) 的两个排列 \(P_1\) 和 \(P_2\) ，求它们的最长公共子序列。
\(1 \le n \le 10^5\)。
没错，这是最长公共子序列的模板题。
在这道题中，由于保证了给定的是两个排列，也就是不存在重复元素，所以我们可以尝试将最长公共子序列问题转化成最长上升子序列问题。
分析这样一组数据。两个序列分别是：
现在尝试把 \(A\) 和 \(B\) 重新标号：
这样的重新标号使得 \(A\) 变成了 \(1 \sim n\)，且如果原来 \(\bm{A_i = B_j}\)，则现在仍然满足 \(\bm {A_i = B_j}\)。
此时，显然 \(A\) 已经变成了一个上升序列，所以 \(A\) 的每个子序列都是上升的。反过来也是满足的，每个上升子序列都是 \(\bm A\) 的子序列（当然，只包含 \(1 \sim n\)）。
这是一条十分重要的性质。那么我们就可以找重新标号后 \(\bm b\) 中的最长上升子序列。
最长上升子序列问题可以使用上面的任意一种方法优化，因此整道题的时间复杂度降到了 \(\Theta(n\log n)\)。
3.4
给定一颗 \(n\) 个点的树，点有点权。请对于每个 \(i\)，求出 \(1\) 号点到 \(i\) 号点的路径上最长上升子序列的长度。
\(2 \le n \le 2 \times 10^5\)，\(1 \le a_i \le 10^9\)。
我们不妨设 \(1\) 号点为根节点，接下来类似 3.1，我们在树上从根开始计算。对于每一个节点 \(i\)，我们需要找在从根到点 \(i\) 的路径上的权值 \(< w_i\) 的点，并计算上升子序列长度。这里可以用树状数组完成这件事情。注意在计算完回溯时，需要恢复现场。注意到我们在计算时用到的树状数组的节点数并不多（约为 \(\log n\)），因此只需要把这几个被用到的节点记录下来即可。
注意需要提前将 \(w_i\) 离散化。
#include <bits/stdc++.h>
using namespace std;
const int N = 200010;
int n, w[N], p[N], a, b;
int h[N], e[N * 2], ne[N * 2], idx = 1;
int len;
int f[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int tr[N];
int lowbit(int x)
{
return x & -x;
}
void modify(int u, int x)
{
for (int i = u; i <= n; i += lowbit(i))
tr[i] = max(tr[i], x);
}
int query(int u)
{
int res = 0;
for (int i = u; i; i -= lowbit(i))
res = max(res, tr[i]);
return res;
}
int gett(int x)
{
return lower_bound(p + 1, p + len + 1, w[x]) - p;
}
void dfs(int u, int fa)
{
for (int i = h[u]; i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
int k = gett(j);
queue<int> v; // 用一个队列存储变化过的值，省去不必要的空间
for (int q = k; q <= n; q += lowbit(q))
v.push(tr[q]);
f[j] = query(k - 1) + 1;
modify(k, f[j]);
dfs(j, u);
for (int q = k; q <= n; q += lowbit(q))
tr[q] = v.front(), v.pop();
}
}
void getv(int u, int fa)
{
for (int i = h[u]; i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
f[j] = max(f[j], f[u]);
getv(j, u);
}
}
int main()
{
cin >> n;
for (int i = 1; i <= n; ++ i ) cin >> w[i], p[i] = w[i];
sort(p + 1, p + n + 1);
len = unique(p + 1, p + n + 1) - p - 1;
for (int i = 1; i < n; ++ i )
{
cin >> a >> b;
add(a, b), add(b, a);
}
modify(gett(1), 1);
f[1] = 1;
dfs(1, -1);
getv(1, -1);
for (int i = 1; i <= n; ++ i ) cout << f[i] << '\n';
return 0;
}
3.5
给定 \(n\) 个操作，每次操作给出 \(l,r\)，并在 \(a\) 序列里依次添加 \(i\in[l,r]\)。
求最后 \(a\) 的最长上升子序列。
\(1 \le n \le 2 \times 10^5\)，\(1 \le l \le r \le 10^9\)。
设计初始 DP：设 \(f_i\) 表示以 \(r_i\) 结尾的最长上升子序列的长度，则对于一个前面的区间 \([l_j, r_j]\)，转移如下：
-
若 \(r_j < l_i\)，也就是两个区间没有交集，那么我们可以直接把 \([l_i, r_i]\) 接到 \([l_j, r_j]\) 后面。即 \(f_i = f_j + r_i - l_i + 1\)；
-
若 \(r_j \ge l_i\)，也就是两个区间存在交集，那么直接把把 \([l_i, r_i]\) 接到 \([l_j, r_j]\) 后面是不可取的，因为这会导致 \([l_i, r_j]\) 这一段区间重复。所以我们需要将这一段区间去掉。即 \(f_i = f_j + (r_i - l_i + 1) - (r_j - l_i + 1) = f_j + r_i - r_j\)。
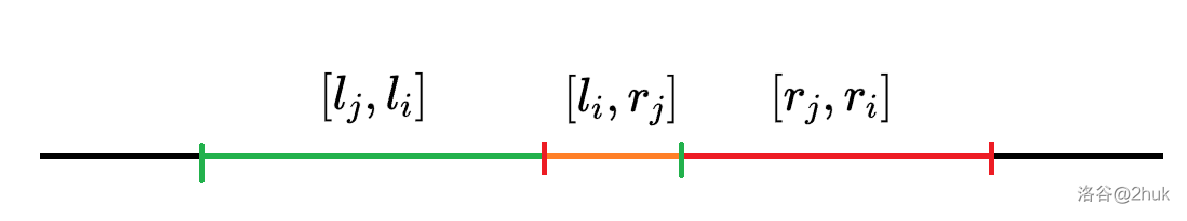
因此总转移为：
直接转移复杂度是 \(\Theta(n^2)\) 的。因此可以数据结构优化，比如线段树。
我们维护两颗线段树，均以 \(r_i\) 作下标，其中第一颗线段树维护 \(f_i\)，第二颗线段树维护 \(f_i - r_i\)。那么转移时这需要在第一颗线段树的 \([1, l_i - 1]\) 的下标内找最大值，并在第二颗线段树的 \([l_i, r_i]\) 找最大值并取更大即可。
计算完后需要在当前下标位置更新。
注意计算前需要离散化。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 400010;
int n, l[N], r[N];
int L[N], R[N], b[N], cnt, len;
int f[N];
struct Tree
{
struct Node
{
int l, r, v;
}tr[N << 2];
#define ls (u << 1)
#define rs (u << 1 | 1)
void pushup(int u)
{
tr[u].v = max(tr[ls].v, tr[rs].v);
}
void build(int u, int l, int r)
{
tr[u] = {l, r, (int)-2e9};
if (l == r) return;
int mid = l + r >> 1;
build(ls, l, mid), build(rs, mid + 1, r);
}
void modify(int u, int x, int d)
{
if (tr[u].l > x || tr[u].r < x) return;
if (tr[u].l == tr[u].r) tr[u].v = max(tr[u].v, d);
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (x <= mid) modify(ls, x, d);
else modify(rs, x, d);
pushup(u);
}
}
int query(int u, int l, int r)
{
if (l > r || tr[u].l > r || tr[u].r < l) return -2e9;
if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;
int mid = tr[u].l + tr[u].r >> 1, res = -2e9;
if (l <= mid) res = query(ls, l, r);
if (r > mid) res = max(res, query(rs, l, r));
return res;
}
}A, B;
main()
{
cin >> n;
for (int i = 1; i <= n; ++ i )
cin >> l[i] >> r[i],
b[ ++ cnt] = l[i], b[ ++ cnt] = r[i];
sort(b + 1, b + cnt + 1);
len = unique(b + 1, b + cnt + 1) - b - 1;
for (int i = 1; i <= n; ++ i )
L[i] = lower_bound(b + 1, b + len + 1, l[i]) - b,
R[i] = lower_bound(b + 1, b + len + 1, r[i]) - b;
A.build(1, 1, len), B.build(1, 1, len);
for (int i = 1; i <= n; ++ i )
{
f[i] = max({
r[i] - l[i] + 1,
A.query(1, 1, L[i] - 1) + r[i] - l[i] + 1,
B.query(1, L[i] + 1, R[i] - 1) + r[i]
});
A.modify(1, R[i], f[i]);
B.modify(1, R[i], f[i] - r[i]);
}
cout << *max_element(f + 1, f + n + 1);
return 0;
}
3.6
给定长度为 \(n\) 的序列 \(a\)，其中有一些数是未知的，这些未知的数为 \(-1\)。
请你为每个未知的数赋值，使得 \(a\) 的严格最长上升子序列最长。求最长的长度。
例如：\(a = \{1, 3, 2, -1, 2\}\)。如果把 \(a_4 = 5\)，那么 \(a\) 的严格最长上升子序列为 \(\{1, 3, 5\}\)。
采用“贪心 + 二分优化 LIS”的方法。
从前往后考虑每个 \(i\)。设 \(f_j\) 表示 \(i\) 之前长度为 \(j\) 的严格最长上升子序列的最小的末尾是多少。然后分情况讨论：
- 如果 \(a_i\) 是确定的：
- 根据上面讲的，二分找到最后一个小于 \(a_i\) 的 \(f_j\)，并将 \(f_{j + 1} = a_i\)。
- 如果 \(a_i\) 是不确定的：
- 考虑如果将它放在某个 \(a_k = j\) 的后面，那么将 \(a_i\) 改为多少比较好呢？
- 我们希望仍然上升，但又不想对后面造成太大影响。所以我们应该将其改成 \(j + 1\)。
- 此时我们并不知道 \(k\) 是多少。但是我们可以在后续用到它的时候，再决定此时的 \(k\)。否则在没用到它的时候，\(a_i\) 是多少都无所谓。
- 所以我们可以对于每个 \(k\) 都计算。也就是对于所有的 \(x\)，将 \(f_{x + 1} = f_x + 1\)。
这个东西是很好做的。第一种情况二分查找，第二种情况只需要记录一下全局加的次数即可。
4. 后言
参考文献：
- 动态规划基础 - OI Wiki；
- stO @gyh 的题解 AcWing 896. 最长上升子序列 II；
- stO @RNTBW 的题解 ARC159D-solution。
