P2542 [AHOI2005] 航线规划
P2542 [AHOI2005] 航线规划
题面
对 Samuel 星球的探险已经取得了非常巨大的成就,于是科学家们将目光投向了 Samuel 星球所在的星系——一个巨大的由千百万星球构成的 Samuel 星系。
星际空间站的 Samuel II 巨型计算机经过长期探测,已经锁定了 Samuel 星系中 \(n\) 个星球的空间坐标,并对这些星球以 \(1\) 至 \(n\) 依次编号。
一些先遣飞船已经出发,在星球之间开辟探险航线。
探险航线是双向的,例如从 \(1\) 号星球到 \(3\) 号星球开辟探险航线,那么从 \(3\) 号星球到 \(1\) 号星球也可以使用这条航线。
例如下图所示:
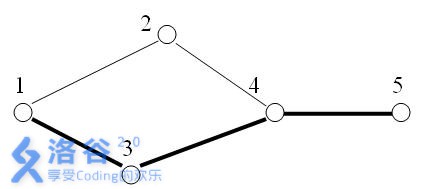
在 \(5\) 个星球之间,有 \(5\) 条探险航线。
\(A,B\) 两星球之间,如果某条航线不存在,就无法从 \(A\) 星球抵达 \(B\) 星球,我们则称这条航线为关键航线。
显然上图中,\(1\) 号与 \(5\) 号星球之间的关键航线有 \(1\) 条:即为 \(4\leftrightarrow5\) 航线。
然而,在宇宙中一些未知的磁暴和行星的冲撞,使得已有的某些航线被破坏,随着越来越多的航线被破坏,探险飞船又不能及时恢复这些航线,可见两个星球之间的关键航线会越来越多。
假设在上图中,航线 $4\leftrightarrow24(从 \(4\) 号星球到 \(2\) 号星球)被破坏。此时,\(1\) 号与 \(5\) 号星球之间的关键航线就有 \(3\) 条:\(1 \leftrightarrow 3\),\(3 \leftrightarrow 4\),\(4 \leftrightarrow 5\)。
小联的任务是,不断关注航线被破坏的情况,并随时给出两个星球之间的关键航线数目。现在请你帮助完成。
输入格式
第一行有两个整数,分别表示星球个数 \(n\) 和初始时的航线条数 \(m\)。
接下来 \(m\) 行,每行有两个不相同的整数 \(u,v\),表示星球 \(u\) 和星球 \(v\) 之间存在一条航线。
接下来有若干行,每行首先给出一个整数 \(op\),表示一次操作的类型。
若 \(op=1\),则后接两个整数 \(u,v\),表示询问当前 \(u,v\) 两星球之间有多少关键航线。
若 \(op=0\),则后接两个整数 \(u,v\),表示 \(u,v\) 之间的航线被破坏。
若 \(op=−1\),则表示输入结束,后面不再存在操作。
输出格式
对每个 \(op=1\) 的询问,输出一行一个整数表示关键航线数目。
输入输出样例
输入
5 5
1 2
1 3
3 4
4 5
4 2
1 1 5
0 4 2
1 5 1
-1
输出
1
3
说明/提示
数据规模与约定
对于全部的测试点,保证:
\(1 \leq n \leq 3 \times 10^4,1 \leq m \leq 10^5\)
$ -1 \leq op \leq 1,1 \leq u, v \leq n$
无论航线如何被破坏,任意时刻任意两个星球都能够相互到达。在整个数据中,任意两个星球之间最多只可能存在一条直接的航线。
对于 \(op=0\) 的操作,保证操作前航线 \(u \leftrightarrow v\) 存在。
询问与破坏航线的总次数不超过 \(4 \times 10^4\)
题解
树上LCA + 并查集 + 树状数组
时间逆序, 变成了加边,
只不过变成了两点之间的桥
还是dfs序的好性质, 记录dfs序和离开当前点的dfs序low, 则 x 的孩子dfs 都大于 dfn[x] 小于等于 low[x]
通过树状数组巧妙维护树形结构 x 到 树根 的距离, 则每次询问就是 ask(x) + ask(y) - 2 * ask(lca(x,y))
关键是加边的时候 怎么维护 x 到根的距离,
跟例题一样, 在并查集爬树的时候, add(dfn[x], 1), add(low[x] + 1, -1) 即可
struct STFrom {
int f[N][20], dep[N], lg[N], t;//N为节点的数量
vector<int>* h;
void init(int n, vector<int>* H) {
t = log2(n - 1) + 1; h = H; lg[0] = -1;
rep(i, 1, n) dep[i] = 0, lg[i] = lg[i >> 1] + 1;
}
void bfs(int s) {
queue<int> q; q.push(s); dep[s] = 1;
rep(i, 0, t) f[s][i] = 0;
while (!q.empty()) {
int x = q.front(); q.pop();
for (auto& y : h[x]) {
if (dep[y]) continue;
dep[y] = dep[x] + 1; f[y][0] = x; q.push(y);
for (int j = 1; j <= t; ++j) f[y][j] = f[f[y][j - 1]][j - 1];
}
}
}
int lca(int x, int y) {
if (dep[x] > dep[y]) swap(x, y);
for (int k = dep[y] - dep[x]; ~lg[k]; k ^= 1 << lg[k]) y = f[y][lg[k]];
if (x == y) return x;
per(i, lg[dep[y]], 0) if (f[x][i] ^ f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
int dist(int x, int y) { return dep[x] + dep[y] - (dep[lca(x, y)] << 1); }
} ST;
struct node { int x, y, op; };
int n, m, _, k, cas;
int f[N], c[N], dfn[N], low[N], df;
PII ed[M];
vector<int> h[N], ans;
vector<node> e;
set<PII> es;
int ff(int x) { return x == f[x] ? x : f[x] = ff(f[x]); }
void add(int x, int k) { for (; x <= n; x += -x & x) c[x] += k; }
int ask(int x) { int ans = 0; for (; x; x -= -x & x) ans += c[x]; return ans; }
void dfs(int x, int fa) {
dfn[x] = ++df;
for (auto& y : h[x]) if (y != fa) dfs(y, x);
low[x] = df;
}
int main() {
IOS; cin >> n >> m; rep(i, 1, n) f[i] = i;
rep(i, 1, m) { cin >> ed[i].fi >> ed[i].se; if (ed[i].fi > ed[i].se) swap(ed[i].fi, ed[i].se); }
stack<node> st;
for (int op, x, y; cin >> op, op != -1;) {
cin >> x >> y; if (x > y) swap(x, y);
if (op == 1) st.push({ x, y, (int)ans.size() }), ans.pb(0);
else st.push({ x, y, -1 }), es.insert({ x, y });
}
rep(i, 1, m) if (!es.count(ed[i]))
if (ff(ed[i].fi) == ff(ed[i].se)) e.push_back({ ed[i].fi, ed[i].se, -1 });
else h[ed[i].fi].pb(ed[i].se), h[ed[i].se].pb(ed[i].fi), f[f[ed[i].fi]] = f[ed[i].se];
ST.init(n, h); ST.bfs(1); dfs(1, 0);
rep(i, 1, n) f[i] = i;// add(dfn[i], ST.dep[i] - 1);
while (!e.empty()) st.push(e.back()), e.pop_back();
while (!st.empty()) {
auto& [x, y, op] = st.top(); st.pop(); int z = ST.lca(x, y);
int fx = ff(x), fy = ff(y), fz = ff(z);
if (op < 0) {
while (fx ^ fz) add(dfn[fx], -1), add(low[fx] + 1, 1), f[fx] = ff(ST.f[fx][0]), fx = f[fx];
while (fy ^ fz) add(dfn[fy], -1), add(low[fy] + 1, 1), f[fy] = ff(ST.f[fy][0]), fy = f[fy];
}
else {
ans[op] = ST.dep[x] + ST.dep[y] - 2 * ST.dep[z];
ans[op] += ask(dfn[x]) + ask(dfn[y]) - 2 * ask(dfn[z]);
}
}
for (auto& i : ans) cout << i << '\n';
return 0;
}


