对称二叉树

题目描述

洛谷（5018）

一棵有点权的有根树如果满足以下条件，则被轩轩称为对称二叉树：

1. 二叉树；
2. 将这棵树所有节点的左右子树交换，新树和原树对应位置的结构相同且点权相等。

下图中节点内的数字为权值，节点外的 idid 表示节点编号。

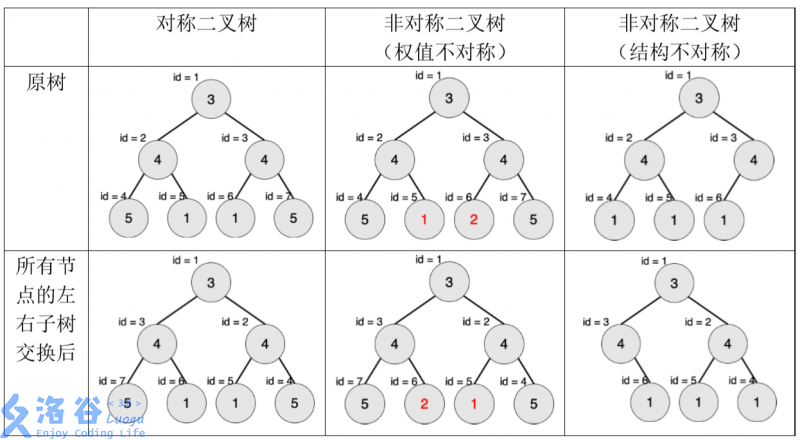
现在给出一棵二叉树，希望你找出它的一棵子树，该子树为对称二叉树，且节点数 最多。请输出这棵子树的节点数。

注意：只有树根的树也是对称二叉树。本题中约定，以节点 TT 为子树根的一棵“子 树”指的是：节点TT 和它的全部后代节点构成的二叉树。

输入输出格式

输入格式：

 

第一行一个正整数 nn，表示给定的树的节点的数目，规定节点编号 1 \sim n1∼n，其中节点 11 是树根。

第二行 nn 个正整数，用一个空格分隔，第 ii 个正整数 v_ivi​ 代表节点 ii 的权值。

接下来 nn 行，每行两个正整数 l_i, r_ili​,ri​，分别表示节点 ii 的左右孩子的编号。如果不存在左 / 右孩子，则以 -1−1 表示。两个数之间用一个空格隔开。

 

输出格式：

 

输出文件共一行，包含一个整数，表示给定的树的最大对称二叉子树的节点数。

思路

1. 建立节点tree结构体，建立结构体数组tree_g[maxa],从i=0:n,将权值放入tree_g[i]

2. 接下来n行两个数a，b，i=1:n，tree_g[i].lift=&tree_g[a]，tree_g[i].right=&tree_g[b]，当a或b为-1，则左孩或右孩为null
3. 检验对称无非是比较另两个节点的权值是否相等，两个节点的第一个的左孩与第二个节点的右孩、第一个的右孩与第二个节点的左孩权值是否相等，直到这两个节点不存在即null，work（tree &a，tree &b）
4. 遍历每个节点，当此节点左孩右孩权值相等，进入work(tree_g[i].lift,tree_g[i].tight),中途加个flag标志当不匹配就不在进行递归，cnt，ans用于记录更新答案

 代码如下：

#include <bits/stdc++.h>
using namespace std;
int n,a,b,flag=1,ans=1,cnt;
struct tree {
    int v;
    tree *l = NULL, *r = NULL;
}tree_g[1000010];
void work(tree *a, tree *b) {
    if (a == NULL&& b == NULL||!flag) return;
    else if (b == NULL|| a == NULL) {flag = 0; return;}
    else if (a->v == b->v) {
        cnt+=2;
        work(a->l, b->r);
        work(a->r, b->l);
    }
    else flag = 0;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)scanf("%d", &tree_g[i].v);
    for (int i = 1; i <= n; ++i) {
        scanf("%d%d", &a, &b);
        if (a != -1)tree_g[i].l = &tree_g[a];
        if (b != -1)tree_g[i].r = &tree_g[b];
    }
    for (int i = 1; i <= n; ++i) {
        if (tree_g[i].l == NULL|| tree_g[i].r == NULL) continue;
        if (tree_g[i].l->v == tree_g[i].r->v) {
            cnt = flag = 1; work(tree_g[i].l, tree_g[i].r);
            if(flag)ans = max(ans, cnt);
        }
    }
    printf("%d", ans);
    return 0;
}