KdTree简介

 参考博客：https://blog.csdn.net/vinceee__/article/details/83044037

参考博客：https://blog.csdn.net/wi162yyxq/article/details/71514423

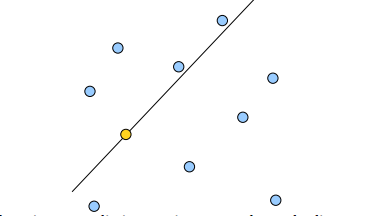
在BSTree中，节点分割的是一维数轴，那么在二维中，节点分割为平面了，就像这样：

 

黄色的点作为根节点，上面的点归左子树，下面的点归右子树，接下来再不断地划分，最后得到一棵树就是的BSPTree（binary space partitioning tree）. 分割的那条线叫做分割超平面（splitting hyperplane），在一维中是一个点，二维中是线，三维的是面。

 

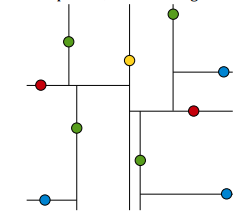
KDTree就是超平面都垂直于轴的BSPTree。同样的数据集，用KDTree划分之后就是这样：

 

KdTree 是以二叉搜索树（Binary Search Tree）为原型的用于空间检索的数据结构，能够在随机分布的空间内以 O(log2N) 的时间复杂度实现对平面内点的搜索以及 O(log2N) + R 的复杂度查询平面内任意矩形内的所有点（R为矩形内点的个数）。 KdTree的应用十分广泛，包括且不限于范围搜索，最邻近点搜索，物理引擎中的碰撞检测以及地理节点（如外卖商家）数据库等。

原理简介
KdTree的实现方法与BST十分相似，以最常用的二维平面的KdTree为例，其每个节点存储一个二维的坐标点，并将平面空间以该点所在的横线/竖线递归地分割成两个子空间。
以width = 1.0, height = 1.0的单位平面为例，依次插入下列点

 

 

 

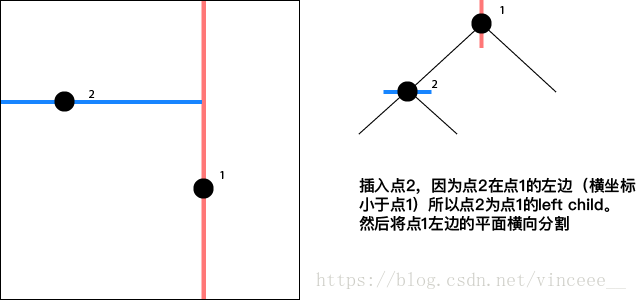
Note:

点对平面的分割方式是横向/纵向按照层次交替出现（根节点是哪个方向都可以）。
插入节点的方法类似于BST，即从根节点开始，（设要插入的节点为Pinsert，当前遍历的节点为Pcurrent）如果Pinsert在Pcurrent的左边或者下边，那么就访问Pcurrent的left child， 反之访问right child直到成为叶子节点。
本KdTree不支持删除操作。

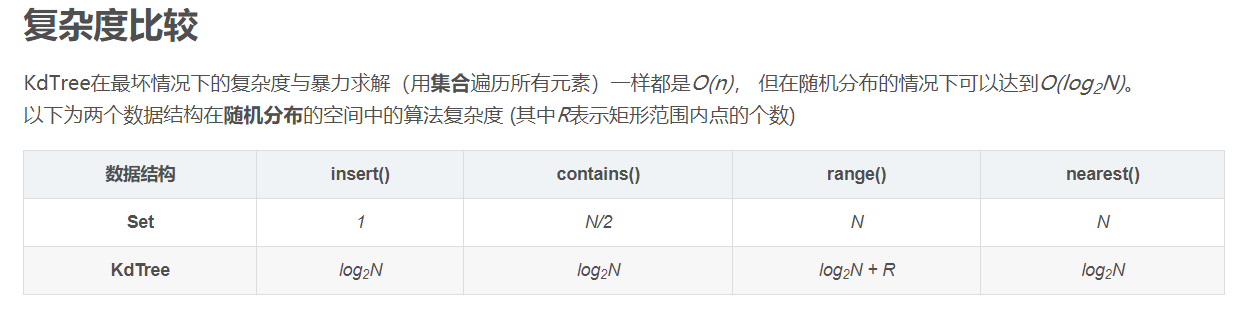
复杂度比较
KdTree在最坏情况下的复杂度与暴力求解（用集合遍历所有元素）一样都是O(n)， 但在随机分布的情况下可以达到O(log2N)。
以下为两个数据结构在随机分布的空间中的算法复杂度 (其中R表示矩形范围内点的个数)