斜率优化
斜率优化
直接看例题
例题：P3195
解析
转移方程很简单：
这里\(f[i]\)表示前\(i\)个物品的最优代价。\(a\)为\(c\)（如题目）的前缀和。
令\(g[i][j]\)表示表示在j处分段，前面按最优方案，后面直到i全部放到1个盒子里的代价。所以：
由于\(a[i],a[j],i,i,L,f[j]\)都为已知量，换元来简化计算。
现在式子就很好看了
还记得\(b[i],f[j],c[j]\)都是常数吗，既然都是常数，那么可以把这个式子理解成\(2b[i]\)为\(k\)（斜率），\(g[i][j]-b[i]^2\)为\(b\)（截距），经过定点\((c[j],f[j]+c[j]^2)\)的一次函数！
斜率一定，且经过定点，那么\(g[i][j]=截距+b[i]\)
这样我们就可以通过图像来分析性质了！
从hhz6830975的题解里盗来的图（侵删）
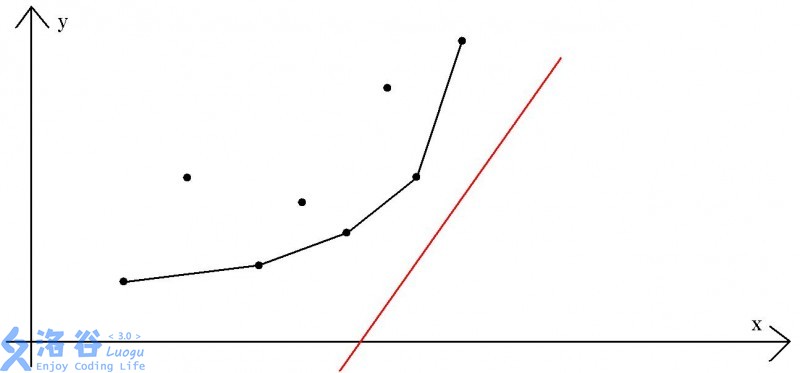
由于我们要找最小的\(g[i][j]\)，所以只有下凸包> 里的点可能有贡献，令\(P[i]\)表式下凸包里，从左到右第i个点。根据凸包的性质，\(P[i],P[i+1]\)的斜率随i递增，那么真正用来转移的点（使截距最大的点）就是第一个让\(P[i],P[i+1]的斜率>=2b[i]\)的点。
总结
所有转移方程可以转化成定斜率的一次函数即具有决策单调性的DP都可以考虑使用斜率优化。
这样的转移方程大多形如：
大概的推导就是把下标为\(i\)的和有\(i\)有\(j\)的扔一边，其他扔对面
始终记住a[i]，b[j]是可以通过下标直接计算得出的常数。
实现
用单调队列的思想实现，注意不同变量的不同单调性。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MM=55000;
ll n,L,c[MM],f[MM],a[MM],q[MM],h,t;
double b(int x)
{
return a[x]+x+L+1;
}
double xl(int x,int y)
{
return (f[x]+b(x)*b(x)-f[y]-b(y)*b(y))/(b(x)-b(y));
}
int main()
{
cin>>n>>L;
for(int i=1;i<=n;i++)
cin>>a[i],a[i]+=a[i-1];
h=t=1;
for(int i=1;i<=n;i++)
{
while(h<t&&xl(q[h],q[h+1])<2*a[i]+2*i)++h;
f[i]=f[q[h]]+(a[i]+i-b(q[h]))*(a[i]+i-b(q[h]));
while(h<t&&xl(q[t-1],q[t])>xl(i,q[t-1]))--t;
q[++t]=i;
}
cout<<f[n];
return 0;
}
再来道例题
\(P_{ix}\)表示第i块的长\(P_{iy}\)表示第i块地的宽，如果存在\(P_{jx}>P_{ix}\)且\(Pjy>Piy\)，那么只要在买含第j块地的一组时顺便把第i块地买了就好，所以第i块地对答案不会有贡献。
考虑所有有贡献的地，将这些地按长升序排序，那么宽一定是降序的。
分析到这可以开始DP了。
\(f[i]\)表示前买前i块地的代价转移方程十分显然：
\(O(n^2)\)肯定过不了，考虑斜率优化。
稍微推下式子:
\(x[i]\)为斜率，过\((-y[j+1],f[j])\)
这次是自己画的图：
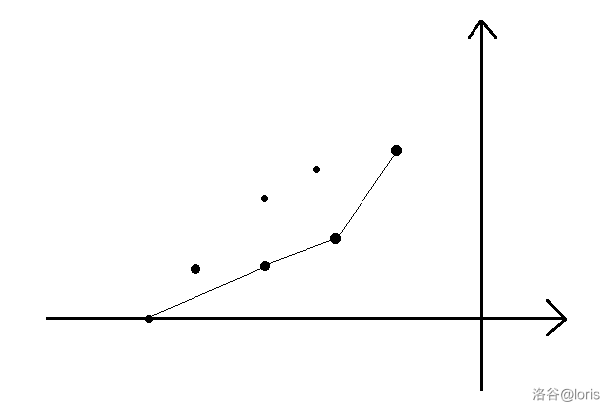
如图，还是一样的维护凸包的过程，但要注意最开始在单调栈插入一个\(0\)即图中\((y[1],0)\)的点，代表把前\(i\)个一次性买了。
实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MM=50004;
struct orzzy
{
int x,y;
}p[MM];
bool cmp(orzzy a,orzzy b)
{
if(a.y==b.y)
return a.x<b.x;
else
return a.y<b.y;
}
int tot,n;
ll f[MM],x[MM],y[MM],tmp,q[MM],h,t;
double xl(int a,int b)
{
return (double)(f[b]-f[a])/(double)(-y[b+1]+y[a+1]);
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
cin>>p[i].x>>p[i].y;
sort(p+1,p+n+1,cmp);
for(int i=n;i>=1;i--)
if(p[i].x>tmp)
tmp=p[i].x,x[++tot]=p[i].x,y[tot]=p[i].y;
n=tot;
h=t=1;
for(int i=1;i<=n;i++)
{
while(h<t&&xl(q[h],q[h+1])<(double)(x[i]))h++;
f[i]=f[q[h]]+y[q[h]+1]*x[i];
while(h<t&&xl(q[t-1],q[t])>xl(q[t-1],i))t--;
q[++t]=i;
}
cout<<f[n];
return 0;
}
