树形dp空间优化（dfn）

树形dp空间优化

介绍

有时题目会告诉我们n叉树的最大层数，或者给出一个完全n叉树树，直接做树形dp会爆空间时，就可以用这个优化方法。

多数树形dp都是先dfs到子树，再合并到根上，显然当合并到根上时子树的信息没有意义了，这就浪费了空间。

举个例子：

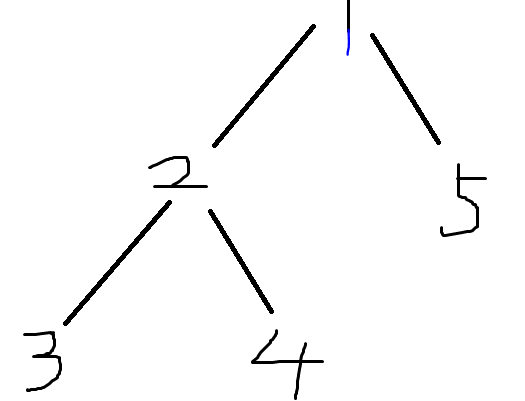
一般的解法会用f[i(1~5)]

但在合并到2后，f[3] f[4]没用了，这时我们就可以用这些空间存5的信息。

实现

定义dfn，注意这里的dfn与dfs需有区别。

以下手动模拟dfs

当前点 dfn

1          1

2          2

3          3

4          4

5          3

每个点的dfn等于父亲的dfn+这是第几个儿子。

5是1的第二个儿子 1+2=3。

此时存i号点信息的就是f[dfn[i]]

f数组一般只要开到(n(最大层数)*m(m叉树))相比起开到总点数小了不少。

例题

P4438 [HNOI/AHOI2018]道路

#include<bits/stdc++.h>
using namespace std;
const int MM=40001;
int s,t,n,a[MM],b[MM],c[MM],son[MM][2],dfn[MM];
long long f[81][41][41];
void dfs(int now,int dep,int Dfn)
{
    //cout<<now<<' '<<Dfn<<endl;
    dfn[now]=Dfn;
    if(now<n)
    {
        dfs(son[now][0],dep+1,dfn[now]+1);
        dfs(son[now][1],dep+1,dfn[now]+2);
        for(int i=0;i<=dep;i++)
            for(int j=0;j<=dep;j++)
                f[dfn[now]][i][j]=min(f[dfn[son[now][0]]][i][j]+f[dfn[son[now][1]]][i][j+1],f[dfn[son[now][0]]][i+1][j]+f[dfn[son[now][1]]][i][j]);
    }
    if(now>=n)
        for(int i=0;i<=dep;i++)
            for(int j=0;j<=dep;j++)
                f[dfn[now]][i][j]=1ll*c[now]*(a[now]+i)*(b[now]+j);
        
}
int main()
{
    cin>>n;
    for(int i=1;i<=n-1;i++)
    {
        cin>>s>>t;
        if(s>0)
            son[i][0]=s;
        else 
            son[i][0]=-s+n-1;
        if(t>0)
            son[i][1]=t;
        else 
            son[i][1]=-t+n-1;
    }
    for(int i=n;i<=2*n-1;i++)
        cin>>a[i]>>b[i]>>c[i];
    dfs(1,1,1);
    cout<<f[1][0][0];
    return 0;
}