一、圆周率π的简介
圆周率用希腊字母 π(读作pài)表示,是一个常数(约等于3.141592654),是代表圆周长和直径的比值。它是一个即无限不循环小数,在日常生活中,通常都用3.14代表圆周率去进行近似计算。
圆周率的求解历程
1965年,英国数学家约翰·沃利斯(John Wallis)出版了一本数学专著,其中他推导出一个公式,发现圆周率等于无穷个分数相乘的积。
2015年,罗切斯特大学的科学家们在氢原子能级的量子力学计算中发现了圆周率相同的公式。
2019年3月14日,谷歌宣布圆周率现已到小数点后31.4万亿位。
二、圆周率的近似计算
1. 计算公式加群:683380553 获取视频教程以及大牛答疑机会!

梅钦公式:

π=圆周长/直径
π=圆面积/半径平方
计算π的方法还有很多种,在这里我就不一一列举了。
在下面的程序中,我采用梅钦方法来计算圆周率。
二丶圆周率的计算方法
蒙特·卡罗方法(Monte Carlo method),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。
代码如下:
import math
import time
scale=14
s,m,=1,2
print("执行开始".center(scale//2, "-"))
start = time.perf_counter()
for i in range(scale+1):
s=math.sqrt((1-math.sqrt(1-pow(s,2)))/2)
m=m*2
a = '*' * i
b = '.' * (scale - i)
c = (i/scale)*100
dur = time.perf_counter() - start
print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,dur))
time.sleep(0.1)
Pi=s*m
print("Pi值是{}".format(Pi))
print("\n"+"执行结束".center(scale//2,'-'))
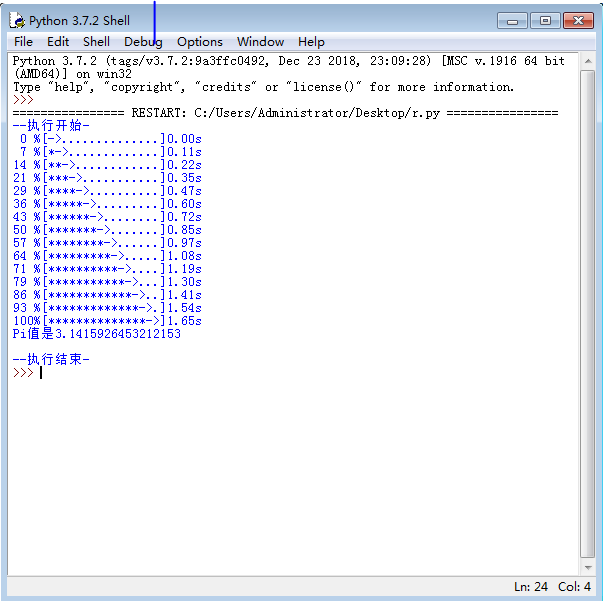
到这里就结束啦



