最优化算法最速下降法、牛顿法、拟牛顿法 Python实现

---------------------------------------2020.9.23更新---------------------------------

把 BFGS(x)改写了一下，变简洁了

def BFGS(x):   #拟牛顿法
    epsilon, h, maxiter = 10**-5, 10**-5, 10**4
    Bk = np.eye(x.size)
    for iter1 in range(maxiter):
        grad = num_grad(x, h)
        if np.linalg.norm(grad) < epsilon:
            return x
        dk = -np.dot((np.linalg.inv(Bk)), grad)
        ak = linesearch(x, dk)
        x = x + dk*ak
        yk = num_grad(x, h) -grad
        sk = ak*dk
        if np.dot(yk, sk) > 0:
            Bs = np.dot(Bk,sk)
            ys = np.dot(yk,sk)
            sBs = np.dot(np.dot(sk,Bk),sk) 
            Bk = Bk - 1.0*Bs.reshape((n,1))*Bs/sBs + 1.0*yk.reshape((n,1))*yk/ys   
    return x

---------------------------------------2020.9.23更新---------------------------------

 

 

只用到了numpy这一个库，只要安装有这个库应该都可以直接运行

import numpy as np

def f(x):   #目标函数
    x1 = x[0]
    x2 = x[1]
    y = 100*((x2 - x1**2)**2) + (x1-1)**2
    return y

def num_grad(x, h):     #求梯度
    df = np.zeros(x.size)
    for i in range(x.size):
        x1, x2 = x.copy(), x.copy()  #这里需要用到复制，而不能用赋值号（=），原因是Python里面=号只是取别名，不是复制（c/c++里面是）
        x1[i] = x[i] - h
        x2[i] = x[i] + h
        y1, y2 = f(x1), f(x2)
        df[i] = (y2-y1)/(2*h)
    return df

def num_hess(x, h):    #求hess矩阵
    hess = np.zeros((x.size, x.size))
    for i in range(x.size):
        x1 = x.copy()
        x1[i] = x[i] - h
        df1 = num_grad(x1, h)
        x2 = x.copy()
        x2[i] = x[i] + h
        df2 = num_grad(x2, h)
        d2f = (df2 - df1) / (2 * h)   
        hess[i] = d2f     
    return hess
    
def linesearch(x, dk):   #求步长
    ak = 1
    for i in range(20):
        newf, oldf = f(x + ak * dk), f(x)
        if newf < oldf:
            return ak
        else:
            ak = ak / 4  #迭代更新步长，步长可随意变换，保证newf比oldf小就可以了（如改为: ak=ak/2 也是可以的）
    return ak

def steepest(x):   #最速下降法
    epsilon, h, maxiter = 10**-5, 10**-5, 10**4
    for iter1 in range(maxiter):
        grad = num_grad(x, h)
        if np.linalg.norm(grad) < epsilon:
            return x
        dk = -grad
        ak = linesearch(x, dk)
        x = x + ak * dk
    return x

def newTonFuction(x):   #牛顿法
    epsilon, h1, h2, maxiter = 10**-5, 10**-5, 10**-5, 10**4
    for iter1 in range(maxiter):
        grad = num_grad(x, h1)
        if np.linalg.norm(grad) < epsilon:
            return x
        hess = num_hess(x, h2)
        dk = -np.dot((np.linalg.inv(hess)), grad)
        x = x + dk
    return x

def BFGS(x):   #拟牛顿法
    epsilon, h, maxiter = 10**-5, 10**-5, 10**4
    Bk = np.eye(x.size)
    for iter1 in range(maxiter):
        grad = num_grad(x, h)
        if np.linalg.norm(grad) < epsilon:
            return x
        dk = -np.dot((np.linalg.inv(Bk)), grad)
        ak = linesearch(x, dk)
        x = x + dk*ak
        yk = num_grad(x, h) -grad
        sk = ak*dk
        if np.dot(yk.reshape(1, grad.shape[0]), sk) > 0:
            '''第一种分步计算实现
            t0 = np.dot(Bk, sk)
            t1 = np.dot(t0.reshape(sk.shape[0], 1), sk.reshape(1, sk.shape[0]))
            temp0 = np.dot(t1, Bk)
            temp1 = np.dot(np.dot(sk.reshape(1, sk.shape[0]), Bk), sk)
            tmp0 = np.dot(yk.reshape(yk.shape[0], 1), yk.reshape(1, yk.shape[0]))
            tmp1 = np.dot(yk.reshape(1, yk.shape[0]), sk)
            Bk = Bk - temp0 / temp1 + tmp0 / tmp1
            '''
            #第二种直接写公式实现
            Bk = Bk - np.dot(np.dot(np.dot(Bk, sk).reshape(sk.shape[0], 1), sk.reshape(1, sk.shape[0])), Bk)/np.dot(np.dot(sk.reshape(1, sk.shape[0]), Bk), sk) + np.dot(yk.reshape(yk.shape[0], 1), yk.reshape(1, yk.shape[0])) / np.dot(yk.reshape(1, yk.shape[0]), sk)
    return x


#x0 = np.array([0.999960983973235, 0.999921911551354])  #初始解
x0 = np.array([0.7, 0.9])    #初始解
x = steepest(x0)     #调用最速下降法
print("最速下降法最后的解向量：",x)
print("最速下降法最后的解：",f(x))
print('')
x = newTonFuction(x0)     #调用牛顿法
print("牛顿法最后的解向量：", x)
print("牛顿法最后的解：", f(x))
print('')
x = BFGS(x0)     #调用拟牛顿法
print("拟牛顿法最后的解向量：", x)
print("拟牛顿法最后的解：", f(x))
print('')

结果如下

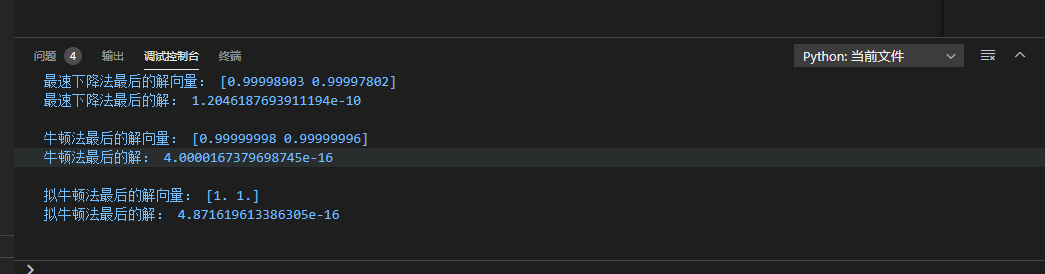
拟牛顿法感觉弄麻烦了，暂时也没想法改，先就这样吧