luogu P8293 [省选联考 2022] 序列变换
因为WC2022考了这种构造，所以下意识将括号序列建树。
手玩一下发现第一个操作实际上是干了这个事情：
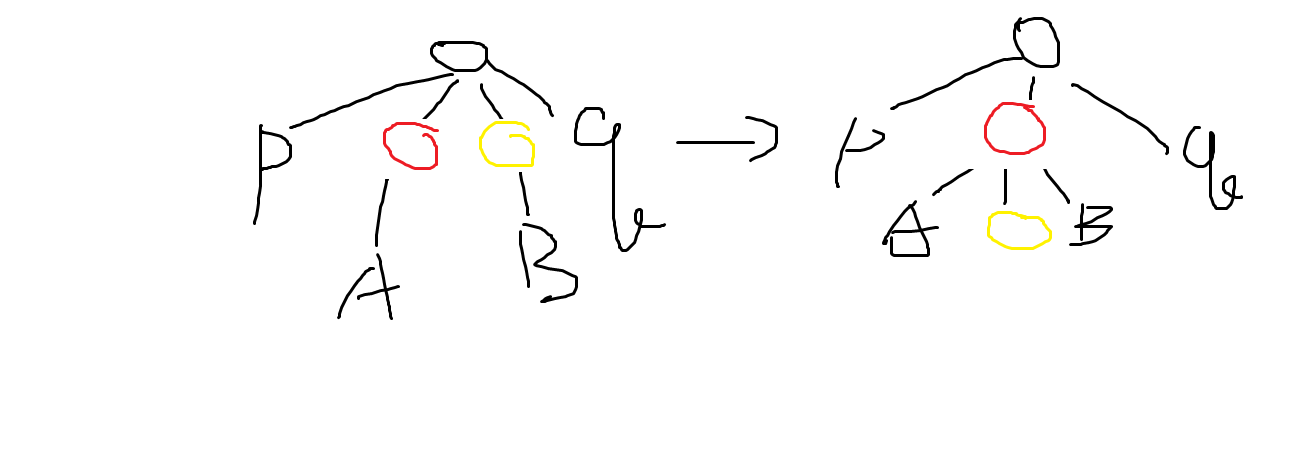
也就是说把用其中一个括号将另一个同层括号在树上移到了下一层。
答案的形式是((((((((()))))))))，也即括号树形成了一条链。
Case 1 :\(X=Y=0\)
显然答案为\(0\)。
Case 2 :\(X=0,Y=1\)
我们要付出被扔到下一层的点的代价。
交换操作可以让我们将同一层的点看作无序。因此往下扔的一定是两个点中更小的点，这样不仅可以让这一层的答案最小，还能让下面的答案尽量小。
用堆维护即可。时间复杂度\(O(n\log n)\)
Case 3 :\(X=1,Y=1\)
可以发现无论我们要往下扔哪个点，都是要付出同样的代价。
因此肯定要把较小的往下扔，可以让下面的答案最小。同时在同一层内最小的要到最后扔，前面用来匹配其他的点最小。
也可以用堆模拟\(O(n\log n)\)。
Case 4 :\(X=1,Y=0\)
我们发现这个情况有点困难，因为我们拿不准到底把较大的点还是较小的点往下扔。
因为较大的点可能不会消耗，但是较小的点可以让下面的点往下的代价更小。
不妨分类讨论，设当前层的点数为\(p\)，若\(p=1\)，直接放在当前层即可。
若\(p>2\)，考虑最多只有一个点内没有贡献，因此第二小的点一定是要有贡献的，而将其放在当前层能只贡献一次，并把一个更小的最小点给送下去。因此是把第二小的点放在当前层。
若\(p=2\)，这个部分比较棘手，但是因为括号序列的层数不可能中间断掉，因此有点的区间是一段前缀。而\(2\)的段数只能有\(2\)段，同时根据上面那套理论我们发现让一个非最大值最小值最后留下是没有意义的，因此最后出来的只有\(2\)种情况，这样可以\(4\)种情况枚举即可。
也是用堆模拟，时间复杂度\(O(n\log n)\)。
code:
#include<bits/stdc++.h>
#define Gc() getchar()
#define Me(x,y) memset(x,y,sizeof(x))
#define Mc(x,y) memcpy(x,y,sizeof(x))
#define d(x,y) ((k+1)*(x)+(y))
#define R(n) (rnd()%(n)+1)
#define Pc(x) putchar(x)
#define LB lower_bound
#define UB upper_bound
#define PB push_back
using ll=long long;using db=double;using lb=long db;using ui=unsigned;using ull=unsigned ll;
using namespace std;const int N=4e5+5,M=1<<13|5,K=400,mod=998244353,Mod=mod-1;const db eps=1e-5;
int n,m,k,x,y,z,a,b;vector<int> S[N];char c[2*N];
namespace Solve1{
ll ToT,Ans;priority_queue<int> Q;void calc(){
int i;for(i=1;i<=n;i++) {for(int j:S[i]) ToT+=j,Q.push(j);ToT-=Q.top();Q.pop();Ans+=ToT;}printf("%lld\n",Ans);
}
}
namespace Solve2{
ll ToT,Ans;int Mi=1e9;priority_queue<int> Q;void calc(){
int i;for(i=1;i<=n;i++) {for(int j:S[i]) ToT+=j,Q.push(j),Mi=min(Mi,j);Ans+=ToT+Mi*(Q.size()-2);ToT-=Q.top();Q.pop();}printf("%lld\n",Ans);
}
}
namespace Solve3{
ll Ans;priority_queue<int,vector<int>,greater<int> > Q;
ll Qry(int x,priority_queue<int,vector<int>,greater<int> > Q){
ll Ans=0,ToT=0;for(int i=x;i<=n;i++){for(int j:S[i]) Q.push(j);
if(Q.size()==1) {Q.pop();continue;}
if(Q.size()==2) {
int Mi=Q.top();ToT+=Q.top();Q.pop();int Mx=Q.top();ToT+=Q.top();Q.pop();
i++;while(S[i].size()==1) Mi=min(Mi,S[i][0]),Mx=max(Mx,S[i][0]),ToT+=S[i][0],i++;
Q.push(Mi);ll F1=Qry(i,Q)+ToT-Mi;Q.pop();Q.push(Mx);ll F2=Qry(i,Q)+ToT-Mx;return min(F1,F2)+Ans;
}
else {int Lp=Q.top();Q.pop();Ans+=Q.top()+1ll*Lp*(Q.size()-1);Q.pop();Q.push(Lp);}
}return Ans;
}
void calc(){printf("%lld\n",Qry(1,Q));}
}
int main(){
freopen("1.in","r",stdin);
scanf("%d%d%d",&n,&a,&b);if(!a&&!b){puts("0");return 0;}scanf("%s",c+1);for(int i=1;i<=2*n;i++){x+=(c[i]^'('?-1:1);if(c[i]=='(') scanf("%d",&y),S[x].PB(y);}
if(!a) Solve1::calc();else if(b) Solve2::calc();else Solve3::calc();
}
