luogu P6774 [NOI2020] 时代的眼泪
我是时代的眼泪/kk
首先我们发现这个东西显然不弱于区间顺序对,也就是说复杂度不可能低于根号,所以盲猜是个大常数根号做法。
首先这个东西看到想到容斥,我们要求的东西大概长这样:
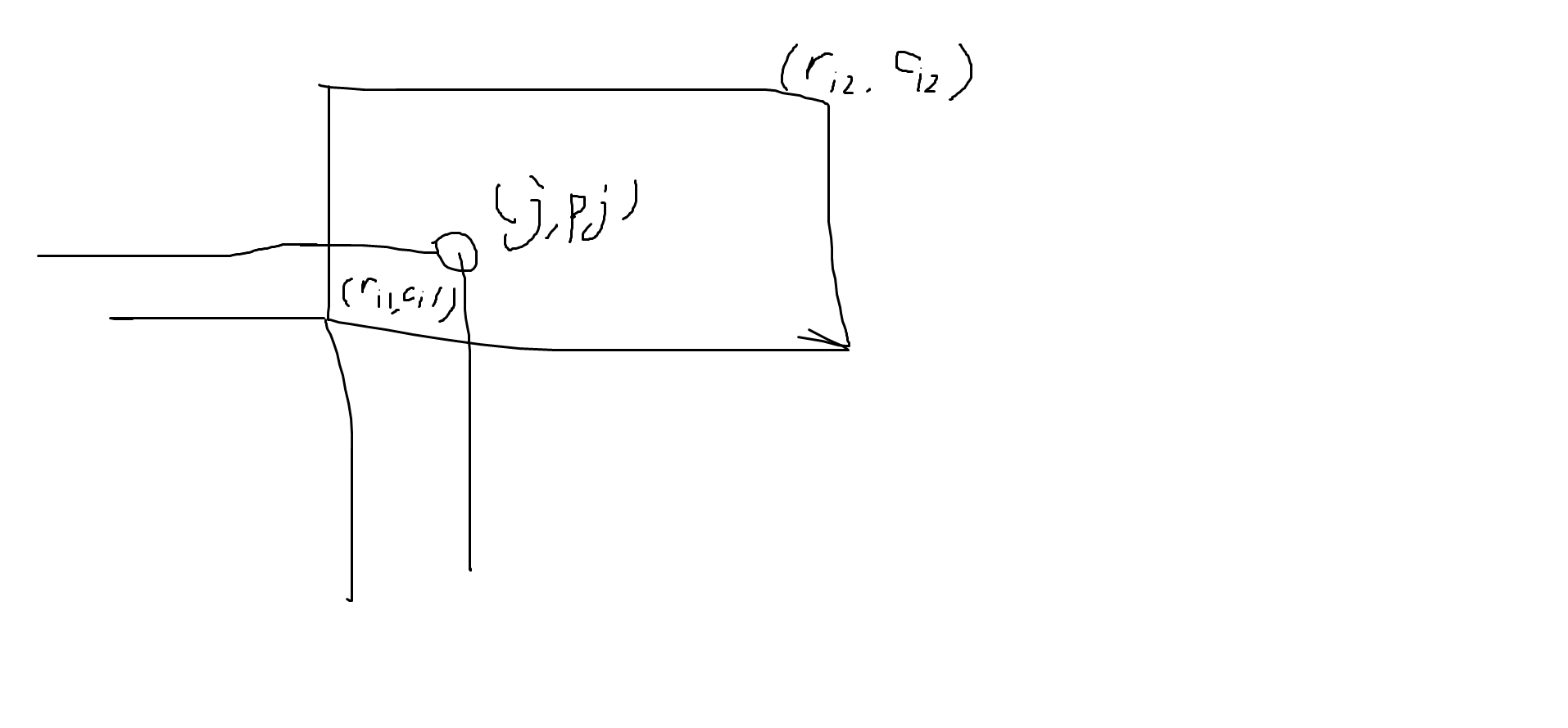
定义\(f(x,y,l,r)\)为\((x,y)\)到\((l,r)\)中的点数,我们对于\(j\)点在\(i\)询问中的答案,我们要求的就是\(f(r_{i,1},c_{i,1},j,p_j)=f(1,j,1,p_j)-f(1,r_{i,1}-1,1,p_j)-f(1,j,1,c_{i,1}-1)+f(1,r_{i,1}-1,1,c_{i,1}-1)\)
其中\(f(1,j,1,p_j)\)随便写个主席树就可以求,\(f(1,r_{i,1}-1,1,c_{i,1}-1)\)对于所有点是一样的也是写个主席树数点即可。剩下两个形式上对称,我们只需考虑其中一个即可。以\(f(1,r_{i,1}-1,1,p_j)\)为例。
首先预处理出一个\(O(n\sqrt n)\)预处理,\(O(1)\)查询的二维数点。设\(B=\sqrt n\),对序列分块,维护整块的前缀和与块内\(O(1)\)离散,因为块内只有\(O(\sqrt n)\)个元素,所以对块内离散后也前缀和,询问时拆开来算即可。
然后因为题目中B部分分提示了莫队,所以我们考虑莫队。
容易发现莫队的时候左端点固定,右端点右移的时候答案容易更新,只要开个值域分块后每个点在前面查到答案后插入值域分块,最后每一问查询对应区间即可。但是左端点移动的时候需要支持对于一段区间中有值的位置都减一,这个不太好\(O(1)\)做出来。
对于这种左端点动不了的莫队,回滚是一种比较优秀的选择。看上去左端点即使回滚也不能添加/删除,但是注意,回滚时询问的值域区间是确定的,也就是说我们左端点的移动可以做到针对这个询问处理答案,假设我们\(l\)往左移动了一个,则这个点增加的贡献是\(f(1,l-1,1,p_l)\),对后面的点减少的贡献是\(f(l+1,r_{i,1},\max(p_l,c_{i,0},c_{i,1}))\)。就可以做到\(O(1)\)计算。
前面的\(f(1,j,1,p_j)\)可以放在这里顺便求掉。另一个将排列置换一下也是一样的做法。
回滚莫队部分时间复杂度\(O(n\sqrt m)\),预处理\(O(n\sqrt n)\),值域分块\(O(m\sqrt n)\),总时间复杂度\(O(m\sqrt n+n(\sqrt n+\sqrt m))\)。
代码其实不难写,3.5k差不多,那种动辄6k的比较吓人。而且如果莫队块长恰当也不卡常,基本上正确性对了lg上就一遍过了。
code:
#include<bits/stdc++.h>
#define I inline
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define abs(x) ((x)>0?(x):-(x))
#define ll long long
#define db double
#define lb long db
#define N (100000+5)
#define M (200000+5)
#define K (350)
#define mod 12345678
#define Mod (mod-1)
#define eps (1e-9)
#define ull unsigned ll
#define it iterator
#define Gc() getchar()
#define Me(x,y) memset(x,y,sizeof(x))
#define Mc(x,y) memcpy(x,y,sizeof(x))
#define d(x,y) ((k+1)*(x)+(y))
#define R(n) (1ll*rand()*rand()%(n)+1)
#define Pc(x) putchar(x)
#define LB lower_bound
#define UB upper_bound
#define PB push_back
using namespace std;
int n,m,k,x,y,z,W[N],A[N],P[N],L[M],R[M],X[M],Y[M];ll Ans[M];
namespace BT{
int k,F[N][K],Q[K][N],La[K][N],Fr[K],En[K];I void BD(){
int i,j,h;k=sqrt(n);for(i=0;i<=n/k;i++){Fr[i]=max(i*k,1),En[i]=min(i*k+k-1,n);
for(j=Fr[i];j<=En[i];j++) Q[i][A[j]]++,La[i][A[j]]++;for(j=1;j<=n;j++) Q[i][j]+=Q[i][j-1]+(i?Q[i-1][j]-Q[i-1][j-1]:0),La[i][j]+=La[i][j-1];
for(j=Fr[i];j<=En[i];j++) for(h=1;h<=En[i]-Fr[i]+1;h++) F[j][h]=(j^Fr[i]?F[j-1][h]:0)+(La[i][A[j]]<=h);
}
}
I int Qry(int x,int y,int L,int R){if(x>y||L>R) return 0;int X=x/k,Y=y/k;if(X==Y) return F[y][La[X][R]]-F[y][La[X][L-1]]+(x^Fr[X]?F[x-1][La[X][L-1]]-F[x-1][La[X][R]]:0);return Q[Y-1][R]-Q[Y-1][L-1]-Q[X][R]+Q[X][L-1]+F[y][La[Y][R]]-F[y][La[Y][L-1]]+F[En[X]][La[X][R]]-F[En[X]][La[X][L-1]]+(x^Fr[X]?F[x-1][La[X][L-1]]-F[x-1][La[X][R]]:0);}
}
struct Ques{int l,r,id;};vector<Ques> S[K<<1];I bool cmp(Ques x,Ques y){return x.r<y.r;}
namespace FK{
int F[N],W[K],k,Fr[K],En[K];I void Cl(){Me(F,0);Me(W,0);}
I void BD(){k=sqrt(n);for(int i=0;i<=n/k;i++) Fr[i]=max(i*k,1),En[i]=min(i*k+k-1,n);}
I void Ins(int x,int w){F[x]+=w;W[x/k]+=w;}
I ll Qry(int x,int y){ll ToT=0;int i;if(x/k==y/k){for(i=x;i<=y;i++) ToT+=F[i];return ToT;}for(i=x;i<=En[x/k];i++) ToT+=F[i];for(i=x/k+1;i<y/k;i++) ToT+=W[i];for(i=Fr[y/k];i<=y;i++) ToT+=F[i];return ToT;}
}
int main(){
freopen("1.in","r",stdin);freopen("1.out","w",stdout);
int i,j;scanf("%d%d",&n,&m);k=max(n/sqrt(m),1);for(i=1;i<=n;i++) scanf("%d",&A[i]),P[A[i]]=i;BT::BD();for(i=1;i<=m;i++){
scanf("%d%d%d%d",&X[i],&Y[i],&L[i],&R[i]);if(X[i]/k==Y[i]/k) {for(j=X[i];j<=Y[i];j++) A[j]>=L[i]&&A[j]<=R[i]&&(Ans[i]+=BT::Qry(X[i],j,L[i],A[j])-1);}
else if(L[i]/k==R[i]/k) {for(j=L[i];j<=R[i];j++) P[j]>=X[i]&&P[j]<=Y[i]&&(Ans[i]+=BT::Qry(X[i],P[j],L[i],j)-1);}
else Ans[i]=1ll*BT::Qry(X[i],Y[i],L[i],R[i])*BT::Qry(1,X[i]-1,1,L[i]-1),S[X[i]/k].PB((Ques){X[i],Y[i],i});
} for(i=1;i<=n;i++) W[i]=BT::Qry(1,i-1,1,A[i]);FK::BD();
for(i=0;i<=n/k;i++){FK::Cl();sort(S[i].begin(),S[i].end(),cmp);
int r=i*k+k-1;for(Ques d:S[i]){
while(r<d.r) ++r,FK::Ins(A[r],W[r]-BT::Qry(1,i*k+k-1,1,A[r]));Ans[d.id]+=FK::Qry(L[d.id],R[d.id]);
for(j=i*k+k-1;j>=d.l;j--) Ans[d.id]+=BT::Qry(j+1,d.r,max(A[j],L[d.id]),R[d.id]),A[j]>=L[d.id]&&A[j]<=R[d.id]&&(Ans[d.id]+=W[j]-BT::Qry(1,j-1,1,A[j]));
}
}for(i=0;i<=n/k;i++) S[i].clear();for(i=1;i<=m;i++)X[i]/k!=Y[i]/k&&L[i]/k!=R[i]/k&&(S[L[i]/k].PB((Ques){L[i],R[i],i}),0);
for(i=0;i<=n/k;i++){FK::Cl();sort(S[i].begin(),S[i].end(),cmp);
int r=i*k+k-1;for(Ques d:S[i]){
while(r<d.r) ++r,FK::Ins(P[r],-BT::Qry(1,P[r],1,i*k+k-1));Ans[d.id]+=FK::Qry(X[d.id],Y[d.id]);
for(j=i*k+k-1;j>=d.l;j--) Ans[d.id]+=BT::Qry(max(P[j],X[d.id]),Y[d.id],j+1,d.r),P[j]>=X[d.id]&&P[j]<=Y[d.id]&&(Ans[d.id]+=-BT::Qry(1,P[j],1,j-1));
}
}for(i=1;i<=m;i++) printf("%lld\n",Ans[i]);
}

