qzezoi 1572 能量收集

题面传送门
这道题的\(dp\)是很好想的，只要从上一行的可以转移的位置转移就好了，时间复杂度\(O(nmt)\),可以有\(80\)分
接下来要优化，有两种思路
思路一:按照上面的状态，我们发现有一个区间求最值的\(O(n)\)复杂度，考虑用单调队列优化掉，因为这个区间向两边延伸，考虑用正反两次单调队列过去，每次单调队列将当前点的上一列的点加入其中，时间复杂度\(O(nm)\)
代码实现:

#include<cstdio>
#define max(a,b) ((a)>(b)?(a):(b))
using namespace std;
int n,m,k,s,f[5039][5039],x,y,z,ans,tot,pus,q[5039],head,tail,a[5039][5039];
int main(){
	register int i,j;
	scanf("%d%d%d%d",&n,&m,&k,&s);
	for(i=1;i<=k;i++) scanf("%d%d%d",&x,&y,&z),a[x][y]=z;
	for(i=1;i<=n;i++){
		head=tail=0;
		for(j=1;j<=m;j++){
			while(q[head+1]+s<j&&head!=tail) head++;
			while(f[i-1][q[tail]]<f[i-1][j]&&head!=tail) tail--;
			q[++tail]=j;
			f[i][j]=f[i-1][q[head+1]];
		}
		head=tail=0;
		for(j=m;j>=1;j--){
			while(q[head+1]>j+s&&head!=tail) head++;
			while(f[i-1][q[tail]]<f[i-1][j]&&head!=tail) tail--;
			q[++tail]=j;
			f[i][j]=max(f[i-1][q[head+1]],f[i][j]);
		}
		//for(j=1;j<=m;j++) printf("%d ",f[i][j]);
		//printf("\n");
		for(j=1;j<=m;j++) f[i][j]+=a[i][j];
	}
	for(i=1;i<=m;i++) ans=max(ans,f[n][i]);
	printf("%d\n",ans);
}

但这道题空间卡的比较紧，要求线性空间，上面过不去，所以考虑滚动，空间复杂度\(O(m)\)，时间复杂度多了一个\(O(klog^2k)\),但和\(dp\)的\(O(nm)\)比起来不算什么
代码实现:

#include<cstdio>
#include<algorithm>
#define max(a,b) ((a)>(b)?(a):(b))
using namespace std;
int n,m,k,s,f[2][5039],x,y,z,ans,tot,pus,q[5039],head,tail,now,last,l=1;
struct yyy{
	int x,y,z;
}fs[5039];
inline bool cmp(yyy x,yyy y){
	return x.x<y.x;
}
int main(){
    register int i,j;
    scanf("%d%d%d%d",&n,&m,&k,&s);
    for(i=1;i<=k;i++) scanf("%d%d%d",&fs[i].x,&fs[i].y,&fs[i].z);
    sort(fs+1,fs+k+1,cmp);
    for(i=1;i<=n;i++){
    	now=i&1;last=(i+1)&1;
        head=tail=0;
        for(j=1;j<=m;j++){
            while(q[head+1]+s<j&&head!=tail) head++;
            while(f[last][q[tail]]<f[last][j]&&head!=tail) tail--;
            q[++tail]=j;
            f[now][j]=f[last][q[head+1]];
        }
        head=tail=0;
        for(j=m;j>=1;j--){
            while(q[head+1]>j+s&&head!=tail) head++;
            while(f[last][q[tail]]<f[last][j]&&head!=tail) tail--;
            q[++tail]=j;
            f[now][j]=max(f[last][q[head+1]],f[now][j]);
        }
        while(fs[l].x==i) f[now][fs[l].y]+=fs[l].z,l++;
		//for(j=1;j<=m;j++) printf("%d ",f[i][j]);
        //printf("\n");
    }
    for(i=1;i<=m;i++) ans=max(ans,f[n&1][i]);
    printf("%d\n",ans);
}

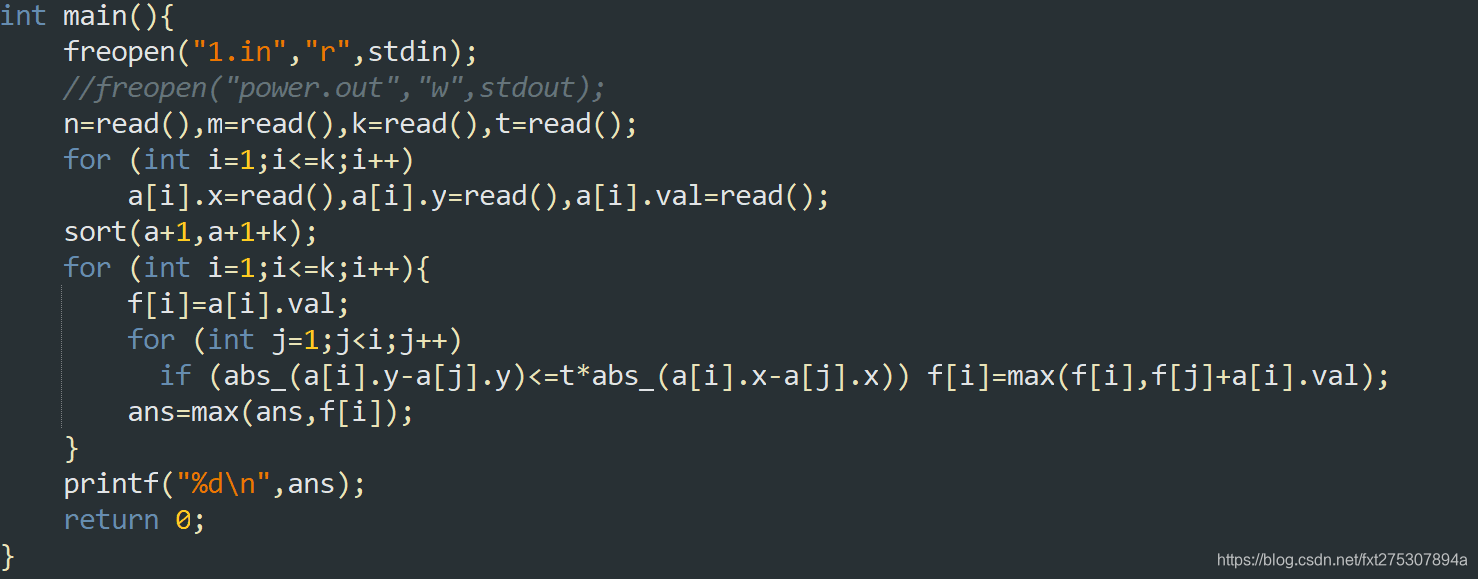
思路二:换一种思路，前面的方法求解了很多没有值的无用状态，考虑直接从有值的状态转移，则先按行列排好序，.对于一个点直接在这个点所覆盖的范围内寻找转移就可以了