把博客园图标替换成自己的图标
把博客园图标替换成自己的图标end

fxtoi FLYing

题面传送门
这是一道主席树的模板题。

很遗憾，被我卡掉了 ----lxl

显然这么小的空间主席树是肯定过不去的，空间复杂度\(O(4nlogn)\)，开满约\(110M\)，只有\(80\)分。
考虑优化。
我们的主席树的划分是这么写的

m=(l+r)>>1

之所以要开四倍空间，是因为会有这样的东西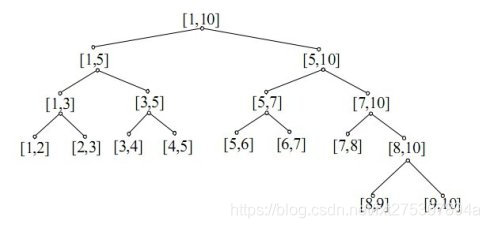在这里插入图片描述所以不能用主席树。
暴力有\(16\)分，暴力枚举+快排即可。
不过常数小也有\(24\)分。
用快排分治找区间第\(k\)大值有\(24\)分。
常数小可以冲\(32\)分。
\(k=1\)有\(32\)分，线段树或\(st\)表求区间最值即可。
没有修改，考虑莫队。
题目给了\(48\)分离线，考虑线段树+莫队，线段树节点上储存所管辖范围内的节点数。可以树上分治。时间复杂度\(O(n\sqrt n logn+mlogn)\)，常数较大，有\(32\)分。
考虑换成树状数组，维护\(a_i\)表示\(1\)到\(i\)的节点数，二分即可。时间复杂度\(O(n\sqrt n logn+mlog^2n)\)，常数较小，有\(40\)分。
考虑去掉移动的\(log\)，考虑单点修改\(O(1)\)的分块。查询在块内分治，时间复杂度\(O((n+m)\sqrt n)\)。可以拿满\(48\)分。
考虑怎么拓展到在线。
可以预处理出\(k\)个节点的信息，对于每个待查询节点左右移动\(\dfrac{n}{k}\)个位置到已知节点，预处理复杂度\(O(nd)\)，查询复杂度\(O(\dfrac{mn}{d})\)，此时\(d\)一般取\(\sqrt n\)最优。时间复杂度\(O((n+m)\sqrt n)\)，空间复杂度\(O(n\sqrt n)\)。有\(64\)分，空间太大了。
题目中说有一部分\(a_i\)各不相同，所以离散后每一位只是\(1\)或\(0\)，考虑\(bitset\)，空间复杂度减少为\(O(\dfrac{n\sqrt n}{w})\)，取\(w\)字长为\(32\)时\(500000\)的数据下空间复杂度约为\(O(nlogn)\)。可以通过没有重复的数据。
考虑有重复的数据咋做，那么我们可以把一样的值散列成不同的值，但映射回去是一样的，就可以解决了。
代码实现:

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<bitset>
#include<cstring> 
using namespace std;
int a[400039],tots[400039],op,lastans,now[400039],last[400039],flag,x,y,z,k,n,m,f[635][635],fxt[400039],sf[635];
bitset<400039> fs[635],ff;
inline void read(int &x){
	char s=getchar();x=0;
	while(s<'0'||s>'9') s=getchar();
	while(s>='0'&&s<='9') x=(x<<3)+(x<<1)+(s^48),s=getchar();
}
inline void print(int x){
	if(x>9) print(x/10);
	putchar(x%10+48);
}
inline bool cmp1(int x,int y){return a[x]<a[y];}
int main(){
	//freopen("flying25.in","r",stdin);
	//freopen("flying25.out","w",stdout);
	register int i,l,r,j,h;
	read(n);read(m);read(op);
	k=sqrt(n);
	for(i=1;i<=k+k/2;i++) last[i]=1;
	for(i=k+k/2+1;i<=n*k/k;i++) last[i]=last[i-k]+1;
	for(i=n/k*k+1;i<=n;i++) last[i]=last[i-1];
	for(i=1;i<=n;i++) read(a[i]),now[i]=i;
	sort(now+1,now+n+1,cmp1);
	for(i=1;i<=n;i++) tots[i]=a[now[i]],a[now[i]]=i;
	for(i=1;i<=n;i++){
		sf[a[i]/k]++;
		ff[a[i]]=1;
		if(i%k==0){
			for(j=0;j<=n/k;j++)f[i/k][j]=sf[j];
			fs[i/k]=ff;
		}
	}
	memset(sf,0,sizeof(sf));
	for(i=1;i<=m;i++){
		read(x),read(y),read(z);
		if(op==2) x^=lastans,y^=lastans;
		l=x;r=y;flag=0;
		while(l<last[x]*k+1){
			sf[a[l]/k]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>last[x]*k+1){
			l--;
			sf[a[l]/k]--;
			fxt[a[l]]--;
		}
		while(r>last[y]*k){
			sf[a[r]/k]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<last[y]*k){
			r++;
			sf[a[r]/k]--;
			fxt[a[r]]--;
		}
		for(j=0; j<=n/k; j++) {
			if(z<=f[last[y]][j]-f[last[x]][j]+sf[j]) {
				for(h=j*k; h<j*k+k; h++) {
					z-=fs[last[y]][h]-fs[last[x]][h]+fxt[h];
					if(z<=0) {flag=h;break;}
				}
				break;
			}
			else z-=f[last[y]][j]-f[last[x]][j]+sf[j];
		}
		print(tots[flag]);putchar('\n');
		lastans=tots[flag];
		while(l<x){
			sf[a[l]/k]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>x){
			l--;
			sf[a[l]/k]--;
			fxt[a[l]]--;
		}
		while(r>y){
			sf[a[r]/k]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<y){
			r++;
			sf[a[r]/k]--;
			fxt[a[r]]--;
		}
	}
}

然后毒瘤出题人会告诉你这样没有切掉，这样你只有\(80\)分，最多\(88\)分。
考虑优化。计算一下时间复杂度，设分为\(d\)块，预处理复杂度为\(O(\dfrac{nd}{32}+d^2)\)，莫队转移复杂度\(O(\dfrac{nm}{d})\)，计算复杂度\(O(m\sqrt n)\)。计算的复杂度是无法通过改变\(d\)来变化的，但其他两个可以。如果\(d\)取\(\sqrt n\)，预处理复杂度是远远小于转移复杂度的。考虑让他们两个一样大，则很明显随着\(d\)的增大转移复杂度是一个反比例函数。要想让\(O(\dfrac{nd}{32}+d^2)=O(\dfrac{nm}{d})\)，那么\(d=\sqrt{32n}\)。即\(d\)在\(d=\sqrt{n}\)到\(d=\sqrt{32n}\)之间时间复杂度都是单调下降的。
但这样子空间就爆了。要\(228M\)。很容易发现到后面增大空间是没有什么意义的。因为这是一个反比例函数，如果将d增加一个单位后比前面时间复杂度减小的值画成一个函数图像，这一定是一个单峰函数。所以一定有一个点使的左边单调上升，右边单调下降。而当这个反比例图像颠倒过来时这个点也是成立的，很明显是取\(d=\sqrt{\sqrt {32} n}\)最优，约为\(2.37\sqrt n\)，总时间复杂度降为\(O(m\sqrt n+\dfrac{n\sqrt n}{32^{\frac{1}{4}}}+\dfrac{n\sqrt n}{32^{\frac{3}{4}}})\)，大的点比原来快了\(1.2s\)
代码实现:

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<bitset>
#include<cstring> 
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
int a[400039],tots[400039],op,ks,lastans,now[400039],last[400039],flag,x,y,z,k,n,m,f[1505][640],fxt[400039],sf[1505];
bitset<400039> fs[1505],ff;
inline void read(int &x){
	char s=getchar();x=0;
	while(s<'0'||s>'9') s=getchar();
	while(s>='0'&&s<='9') x=(x<<3)+(x<<1)+(s^48),s=getchar();
}
inline void print(int x){
	if(x>9) print(x/10);
	putchar(x%10+48);
}
inline bool cmp1(int x,int y){return a[x]<a[y];}
int main(){
	//freopen("flying25.in","r",stdin);
	//freopen("1.out","w",stdout);
	register int i,l,r,j,h,nowx,nowy;
	read(n);read(m);read(op);
	k=(int)(sqrt(n)/2.37);
	ks=sqrt(n);
	for(i=1;i<=k+k/2;i++) last[i]=1;
	for(i=k+k/2+1;i<=n*k/k;i++) last[i]=last[i-k]+1;
	for(i=n/k*k+1;i<=n;i++) last[i]=last[i-1];
	for(i=1;i<=n;i++) read(a[i]),now[i]=i;
	sort(now+1,now+n+1,cmp1);
	for(i=1;i<=n;i++) tots[i]=a[now[i]],a[now[i]]=i;
	for(i=1;i<=n;i++){
		sf[a[i]/ks]++;
		ff[a[i]]=1;
		if(i%k==0){
			for(j=0;j<=n/ks;j++)f[i/k][j]=sf[j];
			fs[i/k]=ff;
		}
	}
	memset(sf,0,sizeof(sf));
	for(i=1;i<=m;i++){
		read(x),read(y),read(z);
		if(op==2) x^=lastans,y^=lastans;
		l=x;r=y;flag=0;
		nowx=last[x]*k+1;nowy=last[y]*k;
		while(l<nowx){
			sf[a[l]/ks]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>nowx){
			l--;
			sf[a[l]/ks]--;
			fxt[a[l]]--;
		}
		while(r>nowy){
			sf[a[r]/ks]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<nowy){
			r++;
			sf[a[r]/ks]--;
			fxt[a[r]]--;
		}
		for(j=0; j<=n/ks; j++) {
			if(z<=f[last[y]][j]-f[last[x]][j]+sf[j]) {
				for(h=j*ks; h<j*ks+ks; h++) {
					z-=fs[last[y]][h]-fs[last[x]][h]+fxt[h];
					if(z<=0) {flag=h;break;}
				}
				break;
			}
			else z-=f[last[y]][j]-f[last[x]][j]+sf[j];
		}
		print(tots[flag]);putchar('\n');
		lastans=tots[flag];
		while(l<x){
			sf[a[l]/ks]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>x){
			l--;
			sf[a[l]/ks]--;
			fxt[a[l]]--;
		}
		while(r>y){
			sf[a[r]/ks]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<y){
			r++;
			sf[a[r]/ks]--;
			fxt[a[r]]--;
		}
	}
}

然后你又以为你过了。结果·增加了\(0\)到\(8\)分不等，反正你切不掉。
转换一下。如果\(k=r-l+1\)，那么你查询复杂度将会跑满\(\sqrt n\)
我们将它变成查询第\(1\)大的数，那么就会很快。
运用一个数据分治的方法。常数将为一半。
代码实现:

#include<cstdio>
#include<cmath>
#include<algorithm>
#include<bitset>
#include<cstring>
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC target("avx")
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
int a[400039],tots[400039],op,ks,lastans,now[400039],last[400039],flag,x,y,z,k,n,m,f[1505][640],fxt[400039],sf[1505];
bitset<400039> fs[1505],ff;
inline void read(int &x) {
	char s=getchar();x=0;
	while(s<'0'||s>'9') s=getchar();
	while(s>='0'&&s<='9') x=(x<<3)+(x<<1)+(s^48),s=getchar();
}
inline void print(int x) {
	if(x>9) print(x/10);
	putchar(x%10+48);
}
inline bool cmp1(int x,int y) {
	return a[x]<a[y];
}
int main() {
//	freopen("flying25.in","r",stdin);
//	freopen("1.out","w",stdout);
	register int i,l,r,j,h,nowx,nowy;
	read(n);
	read(m);
	read(op);
	k=(int)(sqrt(n)/2.37);
	ks=sqrt(n);
	for(i=1; i<=k+k/2; i++) last[i]=1;
	for(i=k+k/2+1; i<=n*k/k; i++) last[i]=last[i-k]+1;
	for(i=n/k*k+1; i<=n; i++) last[i]=last[i-1];
	for(i=1; i<=n; i++) read(a[i]),now[i]=i;
	sort(now+1,now+n+1,cmp1);
	for(i=1; i<=n; i++) tots[i]=a[now[i]],a[now[i]]=i;
	for(i=1; i<=n; i++) {
		sf[a[i]/ks]++;
		ff[a[i]]=1;
		if(i%k==0) {
			for(j=0; j<=n/ks; j++)f[i/k][j]=sf[j];
			fs[i/k]=ff;
		}
	}
	memset(sf,0,sizeof(sf));
	for(i=1; i<=m; i++) {
		read(x),read(y),read(z);
		if(op==2) x^=lastans,y^=lastans;
		l=x;
		r=y;
		flag=0;
		nowx=last[x]*k+1;
		nowy=last[y]*k;
		while(l<nowx) {
			sf[a[l]/ks]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>nowx) {
			l--;
			sf[a[l]/ks]--;
			fxt[a[l]]--;
		}
		while(r>nowy) {
			sf[a[r]/ks]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<nowy) {
			r++;
			sf[a[r]/ks]--;
			fxt[a[r]]--;
		}
		if(z<y-x+1-z) {
			for(j=0; j<=n/ks; j++) {
				if(z<=f[last[y]][j]-f[last[x]][j]+sf[j]) {
					for(h=j*ks; h<j*ks+ks; h++) {
						z-=fs[last[y]][h]-fs[last[x]][h]+fxt[h];
						if(z<=0) {
							flag=h;
							break;
						}
					}
					break;
				} else z-=f[last[y]][j]-f[last[x]][j]+sf[j];
			}
		}
		else{
			z=y-x+2-z;
			for(j=n/ks; j>=0; j--) {
				if(z<=f[last[y]][j]-f[last[x]][j]+sf[j]) {
					for(h=j*ks+ks-1; h>=j*ks; h--) {
						z-=fs[last[y]][h]-fs[last[x]][h]+fxt[h];
						if(z<=0) {
							flag=h;
							break;
						}
					}
					break;
				} else z-=f[last[y]][j]-f[last[x]][j]+sf[j];
			}
		}
		print(tots[flag]);
		putchar('\n');
		lastans=tots[flag];
		while(l<x) {
			sf[a[l]/ks]++;
			fxt[a[l]]++;
			l++;
		}
		while(l>x) {
			l--;
			sf[a[l]/ks]--;
			fxt[a[l]]--;
		}
		while(r>y) {
			sf[a[r]/ks]++;
			fxt[a[r]]++;
			r--;
		}
		while(r<y) {
			r++;
			sf[a[r]/ks]--;
			fxt[a[r]]--;
		}
	}
}

接下来是一些很不正经的花絮。
在这里插入图片描述
老师很忙。
在这里插入图片描述
我谔谔
在这里插入图片描述
淦
在这里插入图片描述
众所周知，zkw发明了主席树。

随遇而安。
在这里插入图片描述
因为我是出题人，所以我过了这么多次。
在这里插入图片描述
人傻常数大。
在这里插入图片描述
加强数据的毒瘤
在这里插入图片描述
主席树:我做错了啥?
在这里插入图片描述
咋有人告诉了做法还不会写代码的啊。
在这里插入图片描述
你什么都不会。
在这里插入图片描述
老师叫你选A还是B，你选了个C.
在这里插入图片描述
主席树就是那么强大。
在这里插入图片描述
众所周知，bitset有模板
在这里插入图片描述
加强数据的毒瘤\(\times 2\)
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
众做周知，xp真的很慢，win10真的很快。
在这里插入图片描述
这语文水平......
在这里插入图片描述
洛谷评测机波动真心大。
在这里插入图片描述
加强数据的毒瘤\(\times 3\)
在这里插入图片描述
加强数据的毒瘤\(\times 4\)
在这里插入图片描述
莫队真的是优雅的暴力。
在这里插入图片描述
zyq装弱
在这里插入图片描述
加强数据的毒瘤\(\times 5\)
在这里插入图片描述
洛谷居然是个做公益的。
在这里插入图片描述
出题人很忙。
在这里插入图片描述
加强数据的毒瘤\(\times 6\)
在这里插入图片描述
加强数据的毒瘤\(\times 7\)
主席树:嘤嘤嘤
在这里插入图片描述
有人不会st表的吗?
在这里插入图片描述
好暴力。
在这里插入图片描述
zyq装弱\(\times 2\)
在这里插入图片描述
加强数据的毒瘤\(\times 8\)
在这里插入图片描述
zyq牛逼
在这里插入图片描述
我谔谔。
其实这道题还可以带修的啦，复杂度一样的啦。不过出题人没时间打了qwq。

posted @ 2020-06-16 18:34  275307894a  阅读(94)  评论(0)  编辑  收藏  举报
浏览器标题切换
浏览器标题切换end