常用的数据结构及对应算法

一：常见的数据结构及算法

1.线性表及其算法

1.1 线性表

       线性表是最基本、最简单、也是最常用的一种数据结构。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。线性表中数据元素之间的关系是一对一的关系，即除了第一个和最后一个数据元素之外，其它数据元素都是首尾相接的

1.2 线性表的常见算法

删掉线性表中的相同元素，并且按升序排列

LinkList DeleteSameElem(LinkList &L){
    LNode *pre=L;
    LNode *p=L->next;
    LNode *s=L;
    while(p!=NULL){
        if(pre->data==p->data)
        {
            s=p;
            pre->next=p->next;            
            p=p->next;
            free(s);//释放相同结点空间
        }
        else{
            p=p->next;//不相等时，后移
            pre=pre->next;
        }
 
    }
    return L;
}

2.栈及其算法

2.1 栈

        栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

2.2 栈的常见算法

2.2.1 入栈

void PushStack(char x)  //入栈
{
    LinkStack *top;
    top = (LinkStack *)malloc(sizeof(LinkStack));
    top->data = x;
    top->next = L;
    L = top;
}

2.2.2 出栈

char PopStack()
{
    char x;
    if(L->next == NULL)
    {
        printf("空栈\n");
        exit(1);
    }
    else {
        LinkStack *top;
        x = L->data;
        top = L;
        L = top->next;
        free(top);
        return x;
    }
}

3.队列及其算法

3.1 队列

        队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

   顺序队列中的溢出现象：

  ① "下溢"现象：当队列为空时，做出队运算产生的溢出现象。“下溢”是正常现象，常用作程序控制转移的条件。

  ②"真上溢"现象：当队列满时，做进栈运算产生空间溢出的现象。“真上溢”是一种出错状态，应设法避免。

  ③"假上溢"现象：由于入队和出队操作中，头尾指针只增加不减小，致使被删元素的空间永远无法重新利用。当队列中实际的元素个数远远小于向量空间的规模时，也可能由于尾指针已超越向量空间的上界而

         不能做入队操作。该现象称为"假上溢"现象。

 循环队列：在实际使用队列时，为了使队列空间能重复使用，往往对队列的使用方法稍加改进：无论插入或删除，一旦rear指针增1或front指针增1 时超出了所分配的队列空间，就让它指向这片连续空间的起始                      位置。自己真从MaxSize-1增1变到0，可用取余运算rear%MaxSize和front%MaxSize来实现。这实际上是把队列空间想象成一个环形空间，环形空间中的存储单元循环使用，用这种方法管理的队列也

                  就称为循环队列。除了一些简单应用之外，真正实用的队列是循环队列。 [2] 

                  在循环队列中，当队列为空时，有front=rear，而当所有队列空间全占满时，也有front=rear。为了区别这两种情况，规定循环队列最多只能有MaxSize-1个队列元素，当循环队列中只剩下一个空存储                      单元时，队列就已经满了。

3.2 队列的常见算法

①初始化队列：Init_Queue(q) ，初始条件：队q 不存在。操作结果：构造了一个空队；

②入队操作： In_Queue(q,x),初始条件： 队q 存在。操作结果： 对已存在的队列q，插入一个元素x 到队尾，队发生变化；

③出队操作： Out_Queue(q,x)，初始条件: 队q 存在且非空，操作结果： 删除队首元素，并返回其值，队发生变化；

④读队头元素：Front_Queue(q,x)，初始条件: 队q 存在且非空，操作结果： 读队头元素，并返回其值，队不变；

⑤判队空操作：Empty_Queue(q)，初始条件： 队q 存在，操作结果： 若q 为空队则返回为1，否则返回为0。

4.树和二叉树及其算法

4.1 树和二叉树

4.1.1 树

      树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。

      

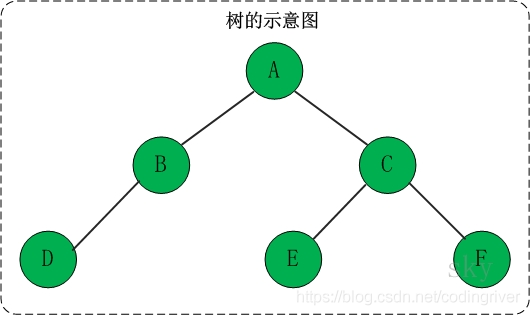
4.1.2 二叉树

      二叉树是每个节点最多有两个子树的树结构。它有五种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左、右子树皆为空。

      

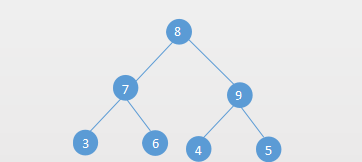
4.2  二叉树的常见算法

前序遍历：前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。在遍历左、右子树时，仍然先访问根节点，然后遍历左子树，最后遍历右子树。

如，下图所示二叉树的遍历结果是：ABDECF

代码实现：

 

private void preorder(Node<T> node) {
    if (node == null) {
        return;
    }
    System.out.println(node.value);
    preorder(node.left);
    preorder(node.right);
}

中序遍历：中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。若二叉树为空则结束返回，否则

如，下图所示二叉树的遍历结果是：DBEAFC

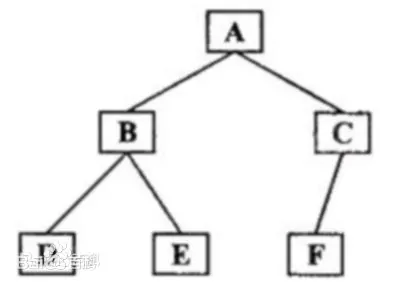
private void inorder(Node<T> node) {
    if (node == null) {
        return;
    }
    inorder(node.left);
    System.out.println(node.value);
    inorder(node.right);
}

后序遍历：后序遍历（LRD）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归和非递归算法两种。在二叉树中，先左后右再根，即首先遍历左子树，然后遍历右子树，最后访                   问根结点。

如，下图所示二叉树的遍历结果是：DEBFCA

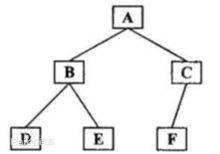
代码实现：

private void postorder(Node<T> node) {
    if (node == null) {
        return;
    }
    postorder(node.left);
    postorder(node.right);
    System.out.println(node.value);
}

5.图及其算法

5.1 图

    在计算机科学中，一个图就是一些顶点的集合，这些顶点通过一系列边结对（连接）。顶点用圆圈表示，边就是这些圆圈之间的连线。顶点之间通过边连接。

 5.1.1 图的分类

 ①无向图： 如果图中任意两个顶点之间的边都是无向边（简而言之就是没有方向的边），则称该图为无向图（Undirected graphs）

 ②有向图：一个有向图D是指一个有序三元组(V(D)，A(D)，ψD)，其中ψD)为关联函数，它使A(D)中的每一个元素(称为有向边或弧)对应于V(D)中的一个有序元素(称为顶点或点)对

 ③完全图：无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。

 ④连通图：任何两个节点之前都是连通的，都存在一条路径，并且图中没有方向。

 ⑥简单图：在图中，若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图。

5.2 图及其常见算法

5.2.1 BFS（广度优先搜索）

     定义：广度优先搜索是最简便的图的搜索算法之一，这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的想。其别名又叫BFS，属于一                 种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。

     代码实现：

void BFS (GRAPH *G , NODE *s) {
    int i;
    NODEQUEUE Q;
    init_queue (&Q , G);
    NODE *temp;
    PTR_NODE *ptr_temp;
 
    for (i = 0 ; i < G->length ; i++) {
        if (arr_V[i] != s) {
            arr_V[i]->color = WHITE;
            arr_V[i]->d = INFINITE;
            arr_V[i]->parent = NULL;
        }
    }
    s->color = GRAY;
    s->parent = NULL;
    s->d = 0;
    enqueue (&Q , s);
 
    while (Q.count != 0) {
        temp = dequeue (&Q);
        ptr_temp = G->adj[temp->key];
        while (ptr_temp != NULL) {
            if (ptr_temp->ptr->color == WHITE) {
                ptr_temp->ptr->color = GRAY;
                ptr_temp->ptr->d = temp->d + 1;
                ptr_temp->ptr->parent = temp;
                enqueue (&Q , ptr_temp->ptr);
            }
            ptr_temp = ptr_temp->next;
        }
        temp->color = BLACK;
    }

5.2.2 DFS (深度优先搜索)

    定义：深度优先搜索是一种在开发爬虫早期使用较多的方法。它的目的是要达到被搜索结构的叶结点 。在一个HTML文件中，当一个超链被选择后，被链接的HTML文件将执行深度优先搜索，即在搜索其余的               超链结果之前必须先完整地搜索单独的一条链。深度优先搜索沿着HTML文件上的超链走到不能再深入为止，然后返回到某一个HTML文件，再继续选择该HTML文件中的其他超链。当不再有其他超链可               选择时，说明搜索已经结束。

   代码实现：

void DFS(ALGraph * alGraph,int v)
{
   int w;
   ArcNode * vexNode;
   visited[v] = 1;
   printf("[%d] -> ",v);
   vexNode = alGraph->vertices[v].firstarc;
   while(vexNode != NULL)
  {
        w = vexNode->adjvex;
        if(visited[w]==0)
        DFS(alGraph,w);
        vexNode = vexNode->nextarc;
       }
}