NOIP的模板--考前复习
距离NOIP还有-1天
可以去放弃一些巨难得题目去搞一些模板了
-------在校老师的原话
一·快排
虽然可以手打,最好用STL,里面有很多优化,会快很多

1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 struct node 5 { 6 int x,y; 7 }a[maxn]; 8 bool cmp(node a,node b) 9 { 10 return a.x<b.x; 11 } 12 int main() 13 { 14 sort(a+1,a+1+n,cmp); 15 return 0; 16 }
二·冰茶姬
一个很好用,很好压行的神奇初级(虽然难题是真的不会)黑科技。

1 int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
三·快速幂||取模运算(就是快速幂里要取模)

1 int KSM(int a,int b,int c) 2 { 3 int ans=1;a%=c; 4 while(b>0) 5 { 6 if(b%2==1)ans=ans*a%c; 7 b/=2;a=a*a%c; 8 } 9 return ans; 10 }
四·线性筛素数
这题有很多方法,比如瞎搞,因为大于10的素数一定都在6的倍数的两边,至于证明什么的可以去找数竞。
或者可以用埃筛(几乎是线性),或者用欧筛
- 以6的倍数来搞事的判断方法:
-
 View Code
View Code1 bool prime(int n) 2 { 3 if(n==1)return false; 4 if(n==2||n==3)return true; 5 if(n%6!=1&&n%6!=5)return false; 6 for(int i=5;i*i<=n;i+=6) 7 if(n%i==0||n%(i+2)==0)retrun false; 8 return true; 9 }
埃筛
-
 View Code
View Code1 void make_prime() 2 { 3 memset(prime,true,sizeof(prime)); 4 prime[0]=prime[1]=false; 5 int t=sqrt(MAXN); 6 for(register int i=2;i<=t;i++)if(prime[i]) 7 for(register int j=2*i;j<MAXN,j+=i) 8 prime[j]=false; 9 }
欧筛
-
 View Code
View Code1 void make_prime() 2 { 3 memset(prime,true,sizeof(prime)); 4 prime[0] = prime[1] = false; 5 for( int i = 2; i <= MAXN; i++) { 6 if( prime[i] ) Prime[ num ++ ] = i; 7 for(int j = 0;j<num && i*Prime[j] < MAXN; j++) { 8 prime[ i*Prime[j] ] = false; 9 if( !( i%Prime[j] ) ) break; 10 } 11 } 12 return; 13 }
还有一些其他搞事的办法,但埃筛,一般就够用了
五·最小生成树
人生信条能打kruskal永远不打prim!!!!!!

1 void kruskal() 2 { 3 int f1,f2,k,i; 4 k=0; 5 for(i=1;i<=n;i++) 6 prt[i]=i; 7 for(i=1;i<=m;i++) 8 { 9 f1=find(a[i].x); 10 f2=find(a[i].y); 11 if(f1!=f2) 12 { 13 ans=ans+a[i].z; 14 prt[f1]=f2; 15 k++; 16 if(k==n-1) 17 break; 18 } 19 } 20 if(k<n-1) 21 { 22 cout<<"orz"<<endl; 23 bj=0; 24 return ; 25 } 26 }
六·单源最短路弱化版(SPFA)
能打SPFA不打dijkstra!!!!!!!!

1 inline void spfa(int k) 2 { 3 queue< int >q; 4 dis[k] = 0; q.push(k); vis[k] = 0; 5 while(!q.empty()) { 6 x = q.front(); q.pop(); vis[x] = 0; 7 for(int i = head[x]; i != 0; i = way[i].next ) { 8 if(dis[x] + way[i].w < dis[way[i].to]) { 9 dis[way[i].to] = dis[x] + way[i].w; 10 if(vis[way[i].to] == 0) { 11 q.push(way[i].to); 12 vis[way[i].to] = 1; 13 } 14 } 15 } 16 } 17 }
七·树状数组

1 int lowbit(int x) 2 { 3 return x&(-x); 4 } 5 int add(int x,int y) 6 { 7 while(x<=n) 8 { 9 c[x]+=y; 10 x+=lowbit(x); 11 } 12 } 13 int sum(int x) 14 { 15 int res=0; 16 while(x>0) 17 { 18 res+=c[x]; 19 x-=lowbit(x); 20 } 21 return res; 22 }
八·乘法逆元
线性的,还有什么费马小,感觉没什么用,就没打

1 int CFNY(int n) 2 { 3 inv[1]=1; 4 cout<<1<<endl; 5 for(int i=2;i<=n;i++) 6 { 7 inv[i]=(long long )(p-p/i)*inv[p%i]%p; 8 cout<<inv[i]<<endl; 9 } 10 }
九·康托展开
绝对没人会在NOIP考这个东西,要是他考了,以后就可以说 这很NOIP。。。。
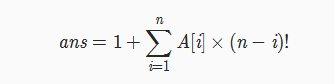

1 ll kangtuo(ll x[]) 2 { 3 ll p=0; 4 for(ll i=1;i<=n;i++) 5 { 6 ll t=0; 7 for(ll j=i+1;j<=n;j++) 8 { 9 if(x[i]>x[j]) 10 { 11 t++; 12 } 13 } 14 p+=t*fc[n-i]; 15 } 16 return p+1; 17 }
十·最近公共祖先(LCA)

1 void dfs(int x,int father)//x为当前节点,father为其父节点 2 { 3 deep[x]=deep[father]+1;//当前点的深度为其父节点深度加1 4 parents[x][0]=father;//当前点的2^0祖先(也就是上1级祖先)就是其父节点 5 for(int i=1;(1<<i)<=deep[x];i++) 6 { 7 parents[x][i]=parents[parents[x][i-1]][i-1]; 8 //这里应该是整个预处理阶段中最有灵魂的部分了 9 //x的2^i级祖先就是x的2^(i-1)级祖先的2^(i-1)级的祖先 。 10 //2^i==2^(i-1)+2^(i-1),这个式子好像没什么可说的 11 } 12 for(int i=head[x];i;i=way[i].next) 13 { 14 int to=way[i].to; 15 if(to!=father) 16 dfs(to,x); 17 } 18 } 19 20 int lca(int a,int b)//a,b为两个要查询的点 21 { 22 if(deep[a]>deep[b])//我时刻保证a的深度比b的小 23 { 24 swap(a,b); //如果反了就换一下 25 } 26 for(int i=20;i>=0;i--) 27 { 28 if(deep[a]<=deep[b]-(1<<i)) 29 b=parents[b][i];//将a和b跳的同一高度 30 } 31 if(a==b)//如果b在跳上来时和a一样了,那说明a就是a和b的LCA,直接返回就行了 32 return a; 33 for(int i=20;i>=0;i--) 34 { 35 if(parents[a][i]==parents[b][i]) 36 continue; 37 else 38 { 39 a=parents[a][i]; 40 b=parents[b][i];//将a和b一起往上跳 41 } 42 } 43 return parents[a][0];//找出最后的答案 44 }
十一·卢卡斯
只存在于组合数里的东西

1 long long CC(long long n,long long m){ 2 if(m>n) 3 return 0; 4 return ((c[n]*KSM(c[m],p-2,p))%p*KSM(c[n-m],p-2,p)%p); 5 } 6 long long Lucas(long long n,long long m){ 7 if(!m) 8 return 1; 9 return CC(n%p,m%p)*Lucas(n/p,m/p)%p; 10 }
十二·二分图匹配

1 int dfs(int t) 2 { 3 for (int i=1; i<=n2; ++i) 4 if (a[t][i] == 1 && check[i] == 0) 5 { 6 check[i] = 1; 7 if (p[i] == 0 || dfs(p[i]) == 1) 8 { 9 p[i] = t; 10 return 1; 11 } 12 } 13 return 0; 14 }
十三·强连通分量(tarjan)

1 void tarjan(int s) 2 { 3 dfn[s]=low[s]=++tim; 4 in[s]=1,stack[++top]=s; 5 for(int i=head[s];i;i=edge[i].next) 6 { 7 int v=edge[i].to; 8 if(!dfn[v]) 9 { 10 tarjan(v); 11 low[s]=min(low[v],low[s]); 12 } 13 else if(in[v]&&low[s]>dfn[v])low[s]=dfn[v]; 14 } 15 if(dfn[s]==low[s]) 16 { 17 int p; 18 belong[s]=++cnt; 19 do 20 { 21 p=stack[top--]; 22 in[p]=0; 23 belong[p]=cnt; 24 }while(p!=s); 25 } 26 }
十四·割点(还是那个有名的tarjan)

1 int tarjan(int x,int y) 2 { 3 low[x]=dfn[x]=++tim; 4 int child=0; 5 for(int i=head[x];i;i=way[i].next) 6 { 7 int v=way[i].to ; 8 if(!dfn[v]) 9 { 10 tarjan(v,y); 11 low[x]=min(low[x],low[v]); 12 if(dfn[x]<=low[v]&&x!=y) 13 { 14 cut[x]=1; 15 } 16 if(x==y) 17 { 18 child++; 19 } 20 } 21 low[x]=min(low[x],dfn[v]); 22 if(child>=2&&x==y) 23 { 24 cut[x]=1; 25 } 26 } 27 }
十五·对拍之造数据(maker)Windows下
eg. 2个正整数x0,y0

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 freopen("data.in","w",stdout); 6 srand(time(NULL)); 7 int n=rand(); 8 int m=rand();//可以在这里加模数来控制范围 9 cout<<n<<" "<<m<<endl; 10 }
十六·对拍之检查(check)Windows下
这个在用之前一定要先把所有的程序先跑一下,然后一定要在同一各根目录下,不然有可能会用一些很神奇的东西把源程序给覆盖掉

1 #include<bits/stdc++.h> 2 using namespace std; 3 int main() 4 { 5 while(1) 6 { 7 system("maker"); 8 system("true"); 9 system("false"); 10 if(system("fc false.out true.out") 11 { 12 cout<<"WA"<<endl; 13 break; 14 } 15 cout<<"AC"<<endl; 16 } 17 return 0; 18 }
十七·缩点(还是那个tarjan)

1 void tarjan(int x) 2 { 3 low[x]=dfn[x]=++tim; 4 stac[++top]=x; 5 vis[x]=1; 6 for(int i=head[x];i;i=edge[i].next) 7 { 8 int v=edge[i].to; 9 if(!dfn[v]) 10 { 11 tarjan(v); 12 low[x]=min(low[x],low[v]); 13 } 14 else if(vis[v]) 15 { 16 low[x]=min(low[x],dfn[v]); 17 } 18 } 19 if(dfn[x]==low[x]) 20 { 21 int y; 22 while(y=stac[top--]) 23 { 24 sd[y]=x; 25 vis[y]=0; 26 if(x==y) 27 break; 28 p[x]+=p[y]; 29 } 30 } 31 }
十八·网络最大流(很NOIP的一个东西)

1 int bfs() 2 { 3 memset(deep,0x3f,sizeof(deep)); 4 memset(in,0,sizeof(in)); 5 deep[s]=0; 6 queue<int >q; 7 q.push(s); 8 while(!q.empty()) 9 { 10 int x=q.front(); 11 q.pop(); 12 in[x]=0; 13 for(int i=head[x];i;i=way[i].next) 14 { 15 int v=way[i].to; 16 if(deep[v]>deep[x]+1&&way[i].value) 17 { 18 deep[v]=deep[x]+1; 19 if(in[v]==0) 20 { 21 q.push(v); 22 in[v]=1; 23 } 24 } 25 } 26 } 27 if(deep[t]!=0x3f3f3f3f) 28 return 1; 29 return 0; 30 } 31 int dfs(int x,int y) 32 { 33 ans=0; 34 if(x==t) 35 return y; 36 for(int i=head[x];i;i=way[i].next) 37 { 38 int v=way[i].to; 39 if(way[i].value&&deep[v]==deep[x]+1) 40 { 41 if(ans=dfs(v,min(y,way[i].value))) 42 { 43 way[i].value-=ans; 44 way[i^1].value+=ans; 45 return ans; 46 } 47 } 48 } 49 return 0; 50 } 51 int dinic() 52 { 53 low=0; 54 while(bfs()) 55 { 56 while(low=dfs(s,inf)) 57 maxnn+=low; 58 } 59 return maxnn; 60 }
十九·最小费用最大流

1 int spfa() 2 { 3 memset(dis,0x3f,sizeof(dis)); 4 memset(pre,0,sizeof(pre)); 5 memset(in,0,sizeof(in)); 6 queue<int >q; 7 q.push(s); 8 in[s]=1; 9 dis[s]=0; 10 while(!q.empty()) 11 { 12 int x=q.front(); 13 q.pop(); 14 in[x]=0; 15 for(int i=head[x];i;i=way[i].next) 16 { 17 int v=way[i].to; 18 int w=way[i].cost; 19 if(way[i].value>0&&dis[v]>dis[x]+w) 20 { 21 dis[v]=dis[x]+w; 22 pre[v].from=x; 23 pre[v].edge=i; 24 if(in[v]==0) 25 { 26 q.push(v); 27 in[v]=1; 28 } 29 } 30 } 31 } 32 return dis[t]!=0x3f3f3f3f; 33 } 34 int ek() 35 { 36 ans=0; 37 cost=0; 38 int mi; 39 int i; 40 while(spfa()) 41 { 42 mi=inf; 43 for(i=t;i!=s;i=pre[i].from) 44 { 45 mi=min(mi,way[pre[i].edge].value); 46 } 47 for(i=t;i!=s;i=pre[i].from) 48 { 49 way[pre[i].edge].value-=mi; 50 way[pre[i].edge^1].value+=mi; 51 } 52 ans+=mi; 53 cost+=mi*dis[t]; 54 } 55 return ans; 56 }
二十·高精度加减乘除模

1 #include <bits/stdc++.h> 2 using namespace std; 3 struct Big 4 { 5 static const int BASE = 100000000; 6 static const int WIDTH = 8; 7 vector<long long> s; 8 Big() 9 { 10 *this = 0; 11 } 12 Big(const int &num) 13 { 14 *this = num; 15 } 16 17 Big operator=(int num) 18 { 19 s.clear(); 20 do 21 { 22 s.push_back(num % BASE); 23 num /= BASE; 24 } while (num > 0); 25 return *this; 26 } 27 Big operator=(const string &str) 28 { 29 s.clear(); 30 int x, len = (str.length() - 1) / WIDTH + 1; 31 for (int i = 0; i < len; i++) 32 { 33 int end = str.length() - i * WIDTH; 34 int start = max(0, end - WIDTH); 35 sscanf(str.substr(start, end - start).c_str(), "%lld", &x); 36 s.push_back(x); 37 } 38 return *this; 39 } 40 bool operator<(const Big &b) 41 { 42 if (s.size() < b.s.size()) 43 return true; 44 if (s.size() > b.s.size()) 45 return false; 46 for (int i = s.size() - 1; i >= 0; i--) 47 { 48 if (s[i] < b.s[i]) 49 return true; 50 if (s[i] > b.s[i]) 51 return false; 52 } 53 return false; 54 } 55 bool operator>=(const Big &b) 56 { 57 return !(*this < b); 58 } 59 bool operator==(const Big &b) 60 { 61 if (s.size() != b.s.size()) 62 return false; 63 for (int i = 0; i < s.size(); i++) 64 if (s[i] != b.s[i]) 65 return false; 66 return true; 67 } 68 Big operator+(const Big &b) 69 { 70 Big c; 71 c.s.clear(); 72 for (int i = 0, g = 0;; i++) 73 { 74 if (g == 0 && i >= s.size() && i >= b.s.size()) 75 break; 76 int x = g; 77 if (i < s.size()) 78 x += s[i]; 79 if (i < b.s.size()) 80 x += b.s[i]; 81 c.s.push_back(x % BASE); 82 g = x / BASE; 83 } 84 return c; 85 } 86 Big operator-(const Big &b) 87 { 88 Big c; 89 c = *this; 90 for (int i = 0; i < c.s.size(); i++) 91 { 92 int tmp; 93 if (i >= b.s.size()) 94 tmp = 0; 95 else 96 tmp = b.s[i]; 97 if (c.s[i] < tmp) 98 { 99 c.s[i + 1] -= 1; 100 c.s[i] += BASE; 101 } 102 c.s[i] -= tmp; 103 } 104 while (c.s.back() == 0 && c.s.size() > 1) 105 c.s.pop_back(); 106 return c; 107 } 108 void operator-=(const Big &b) 109 { 110 *this = *this - b; 111 } 112 Big operator*(const Big &b) 113 { 114 Big c; 115 c.s.resize(s.size() + b.s.size()); 116 for (int i = 0; i < s.size(); i++) 117 for (int j = 0; j < b.s.size(); j++) 118 c.s[i + j] += s[i] * b.s[j]; 119 for (int i = 0; i < c.s.size() - 1; i++) 120 { 121 c.s[i + 1] += c.s[i] / BASE; 122 c.s[i] %= BASE; 123 } 124 while (c.s.back() == 0 && c.s.size() > 1) 125 c.s.pop_back(); 126 return c; 127 } 128 friend istream &operator>>(istream &input, Big &x) 129 { 130 string s; 131 if (!(input >> s)) 132 return input; 133 x = s; 134 return input; 135 } 136 friend ostream &operator<<(ostream &output, const Big &x) 137 { 138 output << x.s.back(); 139 for (int i = x.s.size() - 2; i >= 0; i--) 140 { 141 char buf[20]; 142 sprintf(buf, "%08d", x.s[i]); 143 for (int j = 0; j < strlen(buf); j++) 144 output << buf[j]; 145 } 146 return output; 147 } 148 }; 149 Big Copy(const Big &b, int x) 150 { 151 Big t; 152 t.s.resize(b.s.size() + x); 153 for (int i = 0; i < b.s.size(); i++) 154 t.s[i + x] = b.s[i]; 155 return t; 156 } 157 Big Divide(const Big &a, const Big &b, Big &mod) 158 { 159 Big c; 160 c.s.resize(a.s.size() - b.s.size() + 1); 161 mod = a; 162 int Pow[(int)log2(Big::BASE) + 5]; 163 Pow[0] = 1; 164 for (int i = 1; i <= log2(Big::BASE); i++) 165 Pow[i] = Pow[i - 1] * 2; 166 for (int i = c.s.size() - 1; i >= 0; i--) 167 { 168 Big t; 169 t = Copy(b, i); 170 for (int j = log2(Big::BASE); j >= 0; j--) 171 if (mod >= t * Pow[j]) 172 { 173 c.s[i] += Pow[j]; 174 mod -= t * Pow[j]; 175 } 176 } 177 while (c.s.back() == 0 && c.s.size() > 1) 178 c.s.pop_back(); 179 return c; 180 } 181 Big a, b; 182 int main() 183 { 184 cin >> a >> b; 185 if (a < b) 186 cout << a + b << endl << '-' << b - a << endl<< a * b << endl << 0 << endl << a << endl; 187 else 188 { 189 Big c, d; 190 c = Divide(a, b, d); 191 cout << a + b << endl << a - b << endl << a * b << endl << c << endl << d << endl; 192 } 193 return 0; 194 }
二十一. 最大公约数和最小公倍数

1 int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } 2 int lcm(int a,int b) 3 { 4 a * b / gcd(a, b); 5 }
二十二.简单乘法(防止因为乘数过大而爆long long)和快速幂

1 int muti(int a,int b)//乘法,防止乘数太大爆long long 2 { 3 int ans=0; 4 while(b) 5 { 6 if(b&1) 7 { 8 ans=(ans+a)%mod; 9 } 10 a=(a+a)%mod; 11 b>>=1; 12 } 13 return ans; 14 } 15 int KSM(int a,int b)//快速幂 16 { 17 int ans=1; 18 while(b) 19 { 20 if(b&1) 21 { 22 ans=nuti(ans,a); 23 } 24 a=muti(a,a); 25 b>>=1; 26 } 27 return ans; 28 }
二十三.质因数分解

1 int devide(int x)//质因数分解 2 { 3 for(int i=1;i<=sum&&prime[i]*prime[i]<=x;++i) 4 { 5 while(x%prime[i]==0) 6 { 7 x/=prime[i]; 8 cout<<prime[i]<<" "; 9 } 10 } 11 if(x!=1) 12 { 13 cout<<x<<" "; 14 } 15 16 }
二十四.拓展欧里几德

1 void exgcd(int a,int b,int &x,int &y)//拓展欧里几德 2 { 3 if(!b) 4 { 5 x=1; 6 y=0; 7 return ; 8 } 9 exgcd(b,a%b,y,x); 10 y-=a/b*x; 11 }
二十五.逆元的几种求法
- 快速幂版
1 inv=KSM(x,Mod-2);//逆元 (快速幂版)
- 拓展欧里几德版
1 exgcd(x,Mod,inv,y); 2 inv=(inv+Mod)%Mod; //(x必须与mod互质)
- 线性求逆元,公式版
1 inv[1]=1;//线性公式 2 for(i=2;i<=n;++i) 3 inv[i]=1ll*(Mod-Mod/i)*inv[Mod%i]%Mod;
二十六.floyd

1 int floyd() 2 { 3 for(int k=1;k<=n;k++) 4 { 5 for(int i=1;i<=n;i++) 6 { 7 for(int j=1;j<=n;j++) 8 { 9 a[i][j]=min(a[i][j],a[i][k]+a[k][j]); 10 } 11 } 12 } 13 }
二十七·最短路之几个瞎搞模板

1 void spfa(int s) 2 { 3 int x, y, i; 4 memset(dis, 0x3f, sizeof(dis)); 5 queue<int> q; 6 q.push(s); 7 dis[s] = 0; 8 while (!q.empty()) 9 { 10 x = q.front(); 11 q.pop(); 12 vis[x] = false; 13 for (i = head[x]; i; i = way[i].next) 14 { 15 y = way[i].to; 16 if (dis[y] > dis[x] + way[i].value) 17 { 18 dis[y] = dis[x] + way[i].value; 19 if (!vis[y]) 20 { 21 q.push(y); 22 vis[y] = true; 23 } 24 } 25 } 26 } 27 }

1 priority_queue<pair<int, int>> q; 2 void dijkstra(int s) 3 { 4 int x, y, i; 5 memset(dis, 0x3f, sizeof(dis)); 6 q.push(make_pair(0, s)); 7 dis[s] = 0; 8 while (!q.empty()) 9 { 10 x = q.top().second; 11 q.pop(); 12 for (i = head[x]; i; i = way[i].next) 13 { 14 y = way[i].to; 15 if (dis[y] > dis[x] + way[i].value) 16 { 17 dis[y] = dis[x] + way[i].value; 18 q.push(make_pair(-dis[y], y)); 19 } 20 } 21 } 22 }
二十八· 二分集合

1 int l = 0; 2 int r = maxx; 3 while (l < r) 4 { 5 int mid = (l + r) >> 1; 6 if (check(mid)) 7 { 8 r = mid; 9 } 10 else 11 { 12 l = mid + 1; 13 } 14 }

1 while (l < r) 2 { 3 int mid = (l + r) >> 1; 4 if (check(mid)) 5 { 6 l = mid; 7 } 8 else 9 { 10 r = mid - 1; 11 } 12 }

1 while (l + eps < r) 2 { 3 double mid = (l + r) >> 1; 4 if (check(mid)) 5 { 6 r = mid; 7 } 8 else 9 { 10 l = mid; 11 } 12 }
二十九· 树状数组求逆序对个数

1 for (int i = 1; i <= n; ++i) 2 { 3 cin >> x; 4 add(x, 1); 5 ans += i - sum(x); 6 }
三十·01背包

1 for (i = 1; i <= n; ++i)//背包 n为物品数,m为物品体积 2 { 3 cin >> v >> w; 4 for (j = m; j >= v; --j) 5 f[j] = max(f[j], f[j - v] + w); 6 } 7 cout << f[m] << endl;
三十一·完全背包

1 for (i = 1; i <= n; ++i) 2 { 3 cin >> v >> w; //背包 n为物品数,m为物品体积 4 for (j = v; j <= m; ++j) 5 f[j] = max(f[j], f[j - v] + w); 6 } 7 cout << f[m] << endl;
三十二 ·最长上升子序列

1 d[k = 1] = a[1];//a是原序列,n为长度,k为最长上升子序列的长度 2 for (i = 2; i <= n; ++i) 3 { 4 if (d[k] < a[i]) 5 d[++k] = a[i]; 6 else 7 d[lower_bound(d + 1, d + k + 1, a[i]) - d] = a[i]; 8 } 9 cout << k << endl;
三十三·最长公共子序列长度

1 for (i = 1; i <= n; ++i)//串为a b,长度为n m 2 { 3 for (j = 1; j <= m; ++j) 4 { 5 if (A[i] == B[j]) 6 f[i][j] = f[i - 1][j - 1] + 1; 7 else 8 f[i][j] = max(f[i - 1][j], f[i][j - 1]); 9 } 10 } 11 cout << f[n][m] << endl;
三十三·最长公共上升子序列

1 B[0] = -inf;//一切概念均同上; 2 for (i = 1; i <= n; ++i) 3 { 4 if (B[0] < A[i]) 5 num = f[i - 1][0]; 6 for (j = 1; j <= m; ++j) 7 { 8 if (A[i] == B[j]) 9 f[i][j] = num + 1; 10 else 11 f[i][j] = f[i - 1][j]; 12 if (B[j] < A[i]) 13 num = max(num, f[i - 1][j]); 14 } 15 } 16 int ans = -inf; 17 for (i = 1; i <= m; ++i) 18 ans = max(ans, f[n][i]); 19 printf("%d", ans);
三十四· 倍增求LCA(必背,容易打错,一定要return)

1 int pre() //LCA 2 { 3 for (int j = 1; j <= 18; j++) 4 { 5 for (int i = 1; i <= n; i++) 6 { 7 fa[i][j] = fa[fa[i][j - 1]][j - 1]; 8 } 9 } 10 } 11 int lca(int x) 12 { 13 int i; 14 if (deep[x] < deep[y]) 15 { 16 swap(x, y); 17 } 18 for (int i = 18; ~i; --i) 19 { 20 if (deep[fa[x][i]] >= deep[y]) 21 { 22 x = fa[x][i]; 23 } 24 } 25 if (x == y) 26 { 27 return x; 28 } 29 for (int i = 18; ~i; --i) 30 { 31 if (fa[x][i] != fa[y][i]) 32 { 33 x = fa[x][i]; 34 y = fa[y][i]; 35 } 36 } 37 return fa[x][0]; 38 }
三十五·树的直径(两次dfs就可以了)

1 int dfs(int x) //树的直径 只要两次dfs就可以了。 2 { 3 int i, j; 4 if (ans < d[x]) 5 { 6 ans = d[x]; 7 p = x; 8 } 9 for (int i = head[x]; i; i = way[i].next) 10 { 11 j = v[i]; 12 if (j != father) 13 { 14 d[j] = d[x] += w[i]; 15 dfs(j, x); 16 } 17 } 18 } 19 void solve() 20 { 21 ans = 0; 22 d[1] = 0; 23 dfs(1, 0); 24 ans = 0; 25 d[p] = 0; 26 dfs(p, 0); 27 cout << ans << endl; 28 }
三十六·树的重心

1 void dfs(int x, int father)//树的重心 2 { 3 int i, j; 4 Max[x] = 0, size[x] = 1; 5 for (i = head[x]; i; i = way[i].next) 6 { 7 j = way[i].to; 8 if (j != father) 9 { 10 dfs(j, x); 11 size[x] += size[j]; 12 Max[x] = max(Max[x], size[j]); 13 } 14 } 15 Max[x] = max(Max[x], n - size[x]); 16 if (num > Max[x]) 17 { 18 pos = x; 19 num = Max[x]; 20 } 21 }
三十七·LCA树链剖分版,要稳定一些

1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 using namespace std; 5 const int maxn = 5e5 + 10; 6 7 int num, size[maxn], deep[maxn], fa[maxn], top[maxn], n, m, p, a, b; 8 struct node 9 { 10 int to; 11 int value; 12 int next; 13 }way[maxn<<1]; 14 int tot = 0; 15 int head[maxn]; 16 int add(int x,int y) 17 { 18 way[++tot].next = head[x]; 19 way[tot].to = y; 20 head[x] = tot; 21 } 22 int dfs1(int x) 23 { 24 size[x] = 1; 25 deep[x] = deep[fa[x]] + 1; 26 for (int i = head[x]; i;i=way[i].next) 27 { 28 if(fa[x]!=way[i].to) 29 { 30 fa[way[i].to] = x; 31 dfs1(way[i].to); 32 size[x] += size[way[i].to]; 33 } 34 } 35 } 36 int dfs2(int x) 37 { 38 int maxx = 0; 39 if(!top[x]) 40 { 41 top[x] = x; 42 } 43 for (int i = head[x]; i;i=way[i].next) 44 { 45 if (fa[x] != way[i].to && size[way[i].to] > size[maxx]) 46 { 47 maxx = way[i].to; 48 } 49 } 50 if(maxx) 51 { 52 top[maxx] = top[x]; 53 dfs2(maxx); 54 } 55 for (int i = head[x]; i; i = way[i].next) 56 { 57 if(way[i].to!=maxx&&fa[x]!=way[i].to) 58 { 59 dfs2(way[i].to); 60 } 61 } 62 } 63 int lca(int x,int y) 64 { 65 while(top[x]!=top[y]) 66 { 67 if(deep[top[x]]<deep[top[y]]) 68 { 69 swap(x, y); 70 } 71 x = fa[top[x]]; 72 } 73 if(deep[x]<deep[y]) 74 { 75 return x; 76 } 77 return y; 78 } 79 int main() 80 { 81 ios::sync_with_stdio(false); 82 cin >> n >> m >> p; 83 for (int i = 1; i < n;i++) 84 { 85 cin >> a >> b; 86 add(a, b); 87 add(b, a); 88 } 89 dfs1(p); 90 dfs2(p); 91 for (int i = 1; i <= m;i++) 92 { 93 cin >> a >> b; 94 cout << lca(a, b) << endl; 95 } 96 return 0; 97 }
三十八·字典树
- 存树

1 struct node 2 { 3 int son[26]; 4 int num; 5 } a[maxn];
- 插入

1 void Insert() 2 { 3 int l, i, p = 0; 4 l = strlen(s); 5 for (i = 0; i < l; ++i) 6 { 7 if (a[p].son[s[i] - 'a'] == 0) 8 a[p].son[s[i] - 'a'] = ++t; 9 p = a[p].son[s[i] - 'a']; 10 a[p].num++; 11 12 } 13 }
- 查询

1 int find() 2 { 3 int l, i, p = 0; 4 l = strlen(s); 5 for (i = 0; i < l; ++i) 6 { 7 if (a[p].son[s[i] - 'a'] == 0) 8 return 0; 9 p = a[p].son[s[i] - 'a']; 10 } 11 return a[p].num; 12 }
三十九· 字符串hash

1 long long Hash()//base 是基数 ans 是hash值 l是长度 s[i]是第i个字符 2 { 3 long long ans = 0; 4 for (int i = 0; i < l; ++i) 5 ans = ans * base + s[i]; 6 return ans; 7 }
四十·线段树1

1 #include<iostream> 2 using namespace std; 3 const int maxn = 1e6 + 10; 4 int a[maxn + 2]; 5 struct node 6 { 7 int l, r; 8 long long pre, add; 9 } tree[maxn]; 10 11 void build(int x,int l,int r) 12 { 13 tree[x].l = l; 14 tree[x].r = r; 15 if(l==r) 16 { 17 tree[x].pre = a[l]; 18 return; 19 } 20 int mid = (l + r) >> 1; 21 build(x * 2, l, mid); 22 build(x * 2 + 1, mid + 1, r); 23 tree[x].pre = tree[x * 2].pre + tree[x * 2 + 1].pre; 24 } 25 void spread(int p) 26 { 27 if (tree[p].add) 28 { 29 tree[p * 2].pre += tree[p].add * (tree[p * 2].r - tree[p * 2].l + 1); 30 tree[p * 2 + 1].pre += tree[p].add * (tree[p * 2 + 1].r - tree[p * 2 + 1].l + 1); 31 tree[p * 2].add += tree[p].add; 32 tree[p * 2 + 1].add += tree[p].add; 33 tree[p].add = 0; 34 } 35 } 36 void add(int p, int x, int y, int z) 37 { 38 if (x <= tree[p].l && y >= tree[p].r) 39 { 40 tree[p].pre += (long long)z * (tree[p].r - tree[p].l + 1); 41 tree[p].add += z; 42 return; 43 } 44 spread(p); 45 int mid = tree[p].l + tree[p].r >> 1; 46 if (x <= mid) 47 add(p * 2, x, y, z); 48 if (y > mid) 49 add(p * 2 + 1, x, y, z); 50 tree[p].pre = tree[p * 2].pre + tree[p * 2 + 1].pre; 51 } 52 long long sum(int p, int x, int y) 53 { 54 if (x <= tree[p].l && y >= tree[p].r) 55 return tree[p].pre; 56 spread(p); 57 int mid = tree[p].l + tree[p].r >> 1; 58 long long ans = 0; 59 if (x <= mid) 60 ans += sum(p * 2, x, y); 61 if (y > mid) 62 ans += sum(p * 2 + 1, x, y); 63 return ans; 64 } 65 int main() 66 { 67 int n, m; 68 cin >> n >> m; 69 for (int i = 1;i<=n;i++) 70 { 71 cin >> a[i]; 72 } 73 build(1, 1, n); 74 for (int i = 1;i<=m;i++) 75 { 76 int q, x, y, z; 77 cin >> q; 78 if(q==1) 79 { 80 cin >> x >> y >> z; 81 add(1, x, y, z); 82 } 83 else 84 { 85 cin >> x >> y; 86 cout << sum(1, x, y) << endl; 87 } 88 } 89 return 0; 90 }
四十一·矩阵快速幂

1 #include <iostream> 2 #include <cstring> 3 #define mod 1000000007 4 #define ll long long 5 using namespace std; 6 struct Mat 7 { 8 ll m[101][101]; 9 }; 10 Mat a, e; 11 ll n, p; 12 Mat Mul(Mat x, Mat y) 13 { 14 Mat c; 15 for (int i = 1; i <= n; i++) 16 { 17 for (int j = 1; j <= n; j++) 18 { 19 c.m[i][j] = 0; 20 } 21 } 22 for (int i = 1; i <= n; i++) 23 { 24 for (int j = 1; j <= n; j++) 25 { 26 for (int k = 1; k <= n; k++) 27 { 28 c.m[i][j] = c.m[i][j] % mod + x.m[i][k] * y.m[k][j] % mod; 29 } 30 } 31 } 32 return c; 33 } 34 Mat pow(Mat x, ll y) 35 { 36 Mat ans = e; 37 while (y) 38 { 39 if (y & 1) 40 ans = Mul(ans, x); 41 x = Mul(x, x); 42 y >>= 1; 43 } 44 return ans; 45 } 46 47 int main() 48 { 49 cin >> n >> p; 50 for (int i = 1; i <= n; i++) 51 { 52 for (int j = 1; j <= n; j++) 53 { 54 cin >> a.m[i][j]; 55 } 56 } 57 for (int i = 1; i <= n; i++) 58 { 59 e.m[i][i] = 1; 60 } 61 Mat ans = pow(a, p); 62 for (int i = 1; i <= n; i++) 63 { 64 for (int j = 1; j <= n; j++) 65 { 66 cout << ans.m[i][j] % mod << " "; 67 } 68 cout << endl; 69 } 70 return 0; 71 }
四十二·退役前最后的一次更新 进制转换,10 转其他

1 #include<iostream> 2 #include<cstdio> 3 using namespace std; 4 int n,m; 5 char f[20] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J'}; 6 void zhuan(int n,int m) 7 { 8 if(n==0) 9 { 10 return; 11 } 12 if(n>0||n%m==0) 13 { 14 zhuan(n / m, m); 15 cout << f[n % m]; 16 } 17 else 18 { 19 zhuan(n / m + 1, m); 20 cout << f[-m+n % m]; 21 } 22 23 } 24 int main() 25 { 26 cin >> n; 27 cin >> m; 28 cout << n << "="; 29 zhuan(n, m); 30 cout << "(base" << m << ")" << endl; 31 return 0; 32 }



