数据结构--树链剖分详解
数据结构--树链剖分详解
关于模板题---->传送门
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式
输入格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
说明
时空限制:1s,128M
数据规模:
对于30%的数据: N≤10,M≤10
对于70%的数据: N≤103,M≤103
对于100%的数据: N≤105,M≤105
( 其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233 )
样例说明:
树的结构如下:
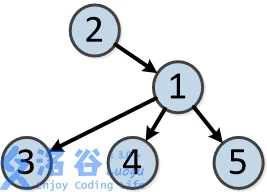
各个操作如下:

故输出应依次为2、21(重要的事情说三遍:记得取模)
开头:
树链剖分,一个在机房里被各位大佬挂在嘴边的算法,其实概念十分简单,就是把一棵树分为很多条链,然后用很多帅(fan)气(ren)的算法去维护这些链,然而度娘的概念是这样的:
树链剖分,计算机术语,指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、SBT、SPLAY、线段树等)来维护每一条链。-------百度百科
由此可见度娘又是也是没啥用的东西,所以就别用了。。。至于树啊,链啊,这些东西,如果,你真的不知道,可以去问度娘(真香)。
必备知识点:
线段树,LCA,前向星存边,dfs序,要是树形DP也会那就更好(我是一直不会)。。。
用到的一些概念:
重边:父节点和他重儿子的连边
重儿子:对于非叶节点,他的儿子中以那个儿子为根的子树节点数最大的儿子为重儿子
轻边:除重边,其余全是轻边
轻儿子:每个非叶节点的儿子中,除去重儿子,其余全是轻儿子
重链:当一条链全为重边组成,其为重链。
注意:
- 对于叶节点,若其为轻儿子,则有一条以自己为起点的长度为一的链。
- 每一条重链均以轻儿子为起点,即为下面提到的TOP。
- 叶节点既没有重儿子,也没有轻儿子,因为他没有儿子。。。
- 每条边的值其实就是进行DFS时的序号。
如图

有关于题目:
- 将树的x到y的最短路径上的所有点都加上z
------>这不是树上拆分的板子题吗?时间复杂度是O(m+n)。
- 求树的x到y的最短路径的所有节点之和
------->LCA!跑一个dfs来处理dis也就O(n)。然后用dis(x,y)=dis(x)+dis(y)-2*dis(LCA)求出答案,好像也不是多难
but
如果两个合在了一起呢?,每次询问都要跑一次DFS,你不炸,谁炸?,所以这个时候就要乖乖打树剖(虽说就是一种暴力优化)
步入主题:
用到的变量(多到令人望而祛步)
1 const int maxn=5e6+10; 2 struct node 3 { 4 int to; 5 int next; 6 }way[maxn];//有关边的结构体 7 struct node2 8 { 9 int l,r,ls,rs; 10 int sum; 11 int lazy; 12 }tree[maxn] ;//线段树用到的结构体 13 int top[maxn];//当前节点所对应链的顶端的点 14 int size[maxn];//当前点的根节点的个数 15 int deep[maxn];//当前点的深度 16 int son[maxn];//当前点的重儿子 17 int r,rt1; 18 int value[maxn];//点的值 19 int rt[maxn];//当前DFS标号在树中的节点 20 int dfsx[maxn];//节点剖分后的新序号(DFS)的执行顺序 21 int n,m,mod,tot; 22 int head[maxn];//领接表存边的好伙伴 23 int father[maxn];//当前点的父节点
实现步骤一一>第一次DFS:
- 对于一个点先找到他的子树大小和他的重儿子(size数组和son数组)
注:如果有一个点有很多个儿子所在的子树大小都一样就随便找一个当重儿子,叶节点没重儿子,非叶节点只有一个重儿子(重要的事情再说一遍)
- 在DFS的过程中可以顺便把每个点的父节点和深度都求出来,说真的我感觉这个DFS和LCA的DFS差不多。
1 void dfs1(int x)//x为当前的点
2 {
3 deep[x]=deep[father[x]]+1;//子节点的深度为其父节点的深度+1
4 size[x]=1;//这个点的本身为1
5 for(int i=head[x];i;i=way[i].next)
6 {
7 int to=way[i].to;
8 if(to!=father[x])
9 {
10 father[to]=x;
11 dfs1(to);//递归子节点
12 size[x]+=size[to];//x的子节点数等于他的+他儿子的
13 if(size[to]>size[son[x]])//如果当前点的子节点数比当前认为的重儿子的子节点数多
14 {
15 son[x]=to;//这个子节点更新为重儿子
16 }
17 }
18 }
19 }
前面的那个图跑完之后大概就会成这样,如果看不懂得可以手动模拟一下,增长印象(手动滑稽),你绝对会记忆深刻
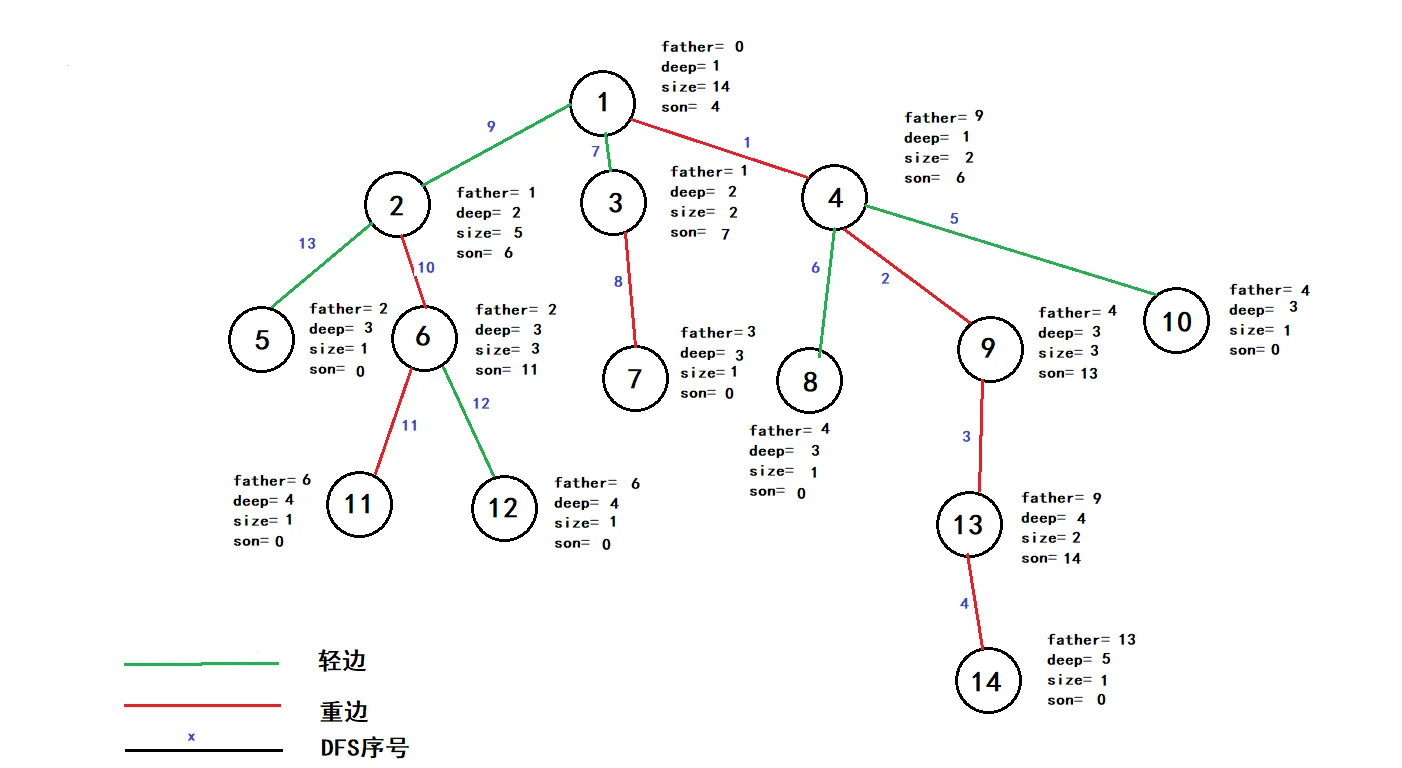
实现步骤一一>第二次DFS
在第二次的DFS中,我们将重边连成重链,然后标记每一个点的DFS序,因为之后要用数据结构来维护这些重链,所以为了方便(主要是懒,这样好打),我们可以让一条重链上的各个节点的DFS序为相邻的数,简单点说就是在这里处理出top数组,rt数组,dfsx数组。
1 void dfs2(int x,int t)//x为当前节点,t为重链的顶端节点
2 {
3 top[x]=t;
4 dfsx[x]=++tot;//标记好DFS序
5 rt[tot]=x;//该DFS序对应的节点
6 if(son[x])
7 {
8 dfs2(son[x],t);//为了方便,我们优先递归重儿子,这样使一条重链上的点DFS序为连续的数
9 //因为是重儿子,所以这一点所在重链的顶端节点还是t
10 }
11 for(int i=head[x];i;i=way[i].next)
12 {
13 int to=way[i].to;
14 if(to!=father[x]&&to!=son[x])
15 {
16 dfs2(to,to);//如果这个点在轻链的底端,那这个他的top必定是它本身
17 }
18 }
19 }
同样在跑完大致就是这样的,如果不懂就自己在画图模拟一下,相信你会对画图软件有更深的认识。。。
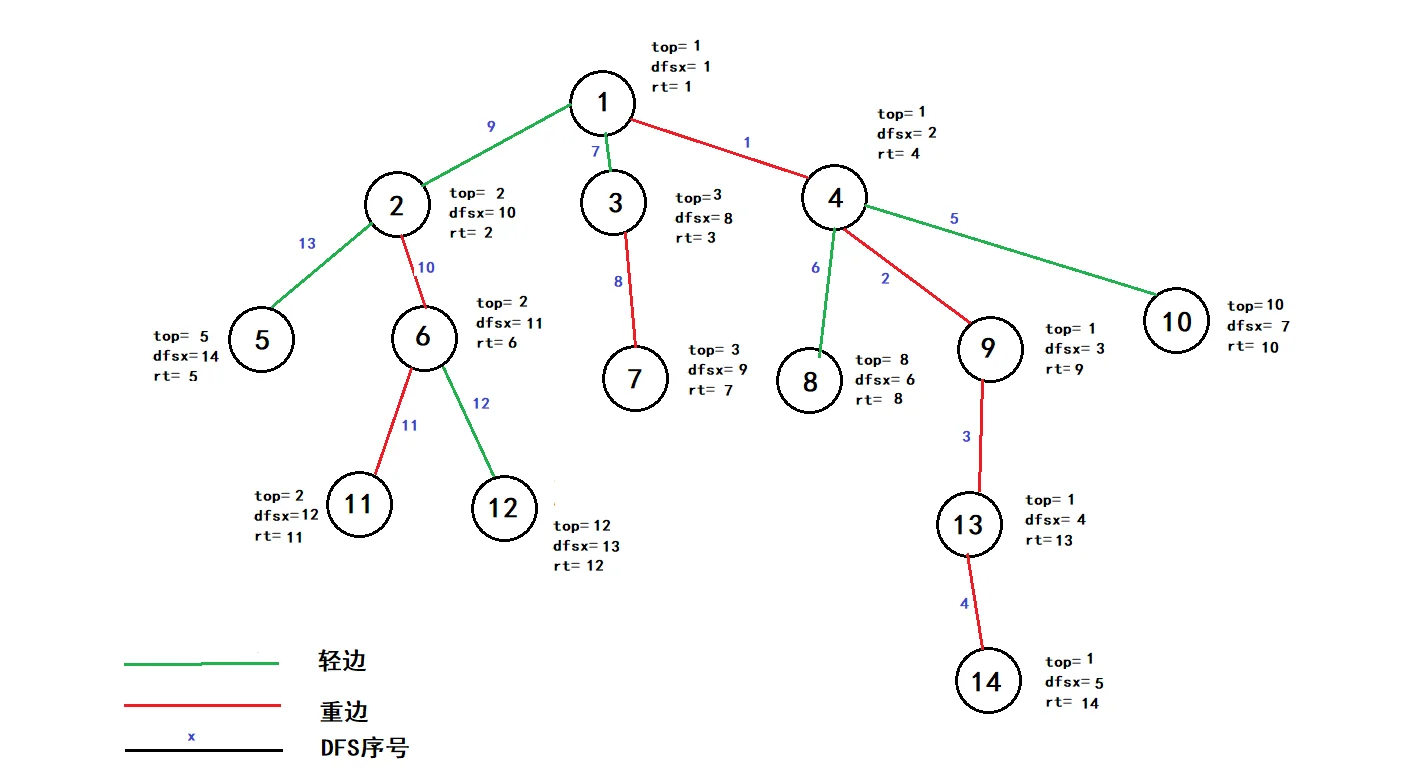
实现步骤一一>维护
以上的两遍DFS是整个树链剖分的精髓,由于我们已经将一条重链上的点的DFS序变成了连续的数,那么下面的维护也就是用数据结构了,最常见的是线段树,当然各种帅(fan)气(ren)的数据结构也可以,所以,数据结构是重点!数据结构是重点!数据结构是重点(重要的事情说三遍),而且最令人兴(yan)奋(wu)的是各种数据结构码量没有少的,所以多打才是熟练的方式,如果你做到像你的文言文那样,无论和时何地都在想编程,那IOI的AU一定是你的!,闲扯结束,回到上面的题目,修改和查询原理差不多,就是一个LCA,但这里有一个TOP这个好东西,可以加速(因为重链可以直接跳到顶部,而轻链的top就是本身),但每次只能跳一次,让更深一点的跳到TOP处,防止因为一起跳而擦肩而过,下面随便加一个ask的代码,其他的根据思路随便改改就可以了
1 int ask(int x,int y)
2 {
3 int res=0;
4 while(top[x]!=top[y])//如果两个点在两条重链上
5 {
6 if(deep[top[x]]<deep[top[y]])
7 {
8 swap(x,y);
9 }
10 res=(res+he(dfsx[top[x]],dfsx[x],rt1))%mod; //线段树的区间求和,来处理重链的贡献
11 x=father[top[x]];//将x换为原链的顶节点,来走轻边
12 }//循环之后,这两个点在同一重链上,但由于不知道是否是同一点,所以来统计一下两点的贡献
13 if(dfsx[x]>dfsx[y])
14 {
15 swap(x,y);
16 }
17 res=(res+he(dfsx[x],dfsx[y],rt1))%mod;
18 return res;
19 }
时间复杂度:
说实话时间复杂度这种东西对于我这样的弱鸡实在没什用,但还是要说一下:
- 因为子节点数最多的儿子为重儿子,所以若(x,y)为轻边,则size[x]<=size[y];
- 因为从根节点到叶节点所经过的轻边数最多,所以由上一条性质得出,每经过一条边,子树的节点个数至少比原来少了一半,所以最多经过log2n条边到叶子==>从根节点到任意节点所经过的重边或轻边的个数一定小于log2n;
- 由以上两点可得出树剖部分的复杂度为O(nlog2n);
完整代码:
这是我打过最长的程序!!!没有之一!!!
1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4
5 using namespace std;
6
7 const int maxn=5e6+10;
8 struct node
9 {
10 int to;
11 int next;
12 }way[maxn];//有关边的结构体
13 struct node2
14 {
15 int l,r,ls,rs;
16 int sum;
17 int lazy;
18 }tree[maxn] ;//线段树用到的结构体
19 int top[maxn];//当前节点所对应链的顶端的点
20 int size[maxn];//当前点的根节点的个数
21 int deep[maxn];//当前点的深度
22 int son[maxn];//当前点的重儿子
23 int r,rt1;
24 int value[maxn];//点的值
25 int rt[maxn];//当前DFS标号在树中的节点
26 int dfsx[maxn];//节点剖分后的新序号(DFS)的执行顺序
27 int n,m,mod,tot;
28 int head[maxn];//领接表存边的好伙伴
29 int father[maxn];//当前点的父节点
30
31 void add(int x,int y)
32 {
33 way[++tot].next=head[x];
34 way[tot].to=y;
35 head[x]=tot;
36 }
37
38 void dfs1(int x)//x为当前的点
39 {
40 deep[x]=deep[father[x]]+1;//子节点的深度为其父节点的深度+1
41 size[x]=1;//这个点的本身为1
42 for(int i=head[x];i;i=way[i].next)
43 {
44 int to=way[i].to;
45 if(to!=father[x])
46 {
47 father[to]=x;
48 dfs1(to);//递归子节点
49 size[x]+=size[to];//x的子节点数等于他的+他儿子的
50 if(size[to]>size[son[x]])//如果当前点的子节点数比当前认为的重儿子的子节点数多
51 {
52 son[x]=to;//这个子节点更新为重儿子
53 }
54 }
55 }
56 }
57
58 void dfs2(int x,int t)//x为当前节点,t为重链的顶端节点
59 {
60 top[x]=t;
61 dfsx[x]=++tot;//标记好DFS序
62 rt[tot]=x;//该DFS序对应的节点
63 if(son[x])
64 {
65 dfs2(son[x],t);//为了方便,我们优先递归重儿子,这样使一条重链上的点DFS序为连续的数
66 //因为是重儿子,所以这一点所在重链的顶端节点还是t
67 }
68 for(int i=head[x];i;i=way[i].next)
69 {
70 int to=way[i].to;
71 if(to!=father[x]&&to!=son[x])
72 {
73 dfs2(to,to);//如果这个点在轻链的底端,那这个他的top必定是它本身
74 }
75 }
76 }
77
78 inline int len(int x)
79 {
80 return tree[x].r-tree[x].l+1;
81 }
82
83 void pushup(int x)
84 {
85 tree[x].sum=(tree[tree[x].ls].sum+tree[tree[x].rs].sum)%mod;
86 }
87
88 void pushdown(int x)
89 {
90 if(tree[x].lazy)
91 {
92 int ls=tree[x].ls;
93 int rs=tree[x].rs;
94 int lz=tree[x].lazy;
95 tree[ls].lazy=(tree[ls].lazy+lz)%mod;
96 tree[rs].lazy=(tree[rs].lazy+lz)%mod;
97 tree[ls].sum=(tree[ls].sum+lz*len(ls))%mod;
98 tree[rs].sum=(tree[rs].sum+lz*len(rs))%mod;
99 tree[x].lazy=0;
100 }
101 }
102
103 void build(int l,int r,int x)
104 {
105 if(l==r)
106 {
107 tree[x].sum=value[rt[l]];
108 tree[x].l=tree[x].r=l;
109 return ;
110 }
111 int mid=(l+r)>>1;
112 tree[x].ls=tot++;
113 tree[x].rs=tot++;
114 build(l,mid,tree[x].ls);
115 build(mid+1,r,tree[x].rs);
116 tree[x].l=tree[tree[x].ls].l;
117 tree[x].r=tree[tree[x].rs].r;
118 pushup(x);
119 }
120
121 void jia(int l,int r,int c,int x)
122 {
123 if(tree[x].l>=l&&tree[x].r<=r)
124 {
125 tree[x].lazy=(tree[x].lazy+c)%mod;
126 tree[x].sum=(tree[x].sum+c*len(x))%mod;
127 return;
128 }
129 pushdown(x);
130 int mid=(tree[x].l+tree[x].r)>>1;
131 if(mid>=l)
132 {
133 jia(l,r,c,tree[x].ls);
134 }
135 if(mid<r)
136 {
137 jia(l,r,c,tree[x].rs);
138 }
139 pushup(x);
140 }
141
142 int he(int l,int r,int x)
143 {
144 if(tree[x].l>=l&&tree[x].r<=r)
145 {
146 return tree[x].sum;
147 }
148 pushdown(x);
149 int res=0;
150 int mid=(tree[x].l+tree[x].r)>>1;
151 if(mid>=l)
152 {
153 res+=he(l,r,tree[x].ls);
154 }
155 if(mid<r)
156 {
157 res+=he(l,r,tree[x].rs);
158 }
159 return res%mod;
160 }
161
162 int ask(int x,int y)
163 {
164 int res=0;
165 while(top[x]!=top[y])//如果两个点在两条重链上
166 {
167 if(deep[top[x]]<deep[top[y]])
168 {
169 swap(x,y);
170 }
171 res=(res+he(dfsx[top[x]],dfsx[x],rt1))%mod; //线段树的区间求和,来处理重链的贡献
172 x=father[top[x]];//将x换为原链的顶节点,来走轻边
173 }//循环之后,这两个点在同一重链上,但由于不知道是否是同一点,所以来统计一下两点的贡献
174 if(dfsx[x]>dfsx[y])
175 {
176 swap(x,y);
177 }
178 res=(res+he(dfsx[x],dfsx[y],rt1))%mod;
179 return res;
180 }
181
182 void jias(int x,int y,int c)
183 {
184 while(top[x]!=top[y])
185 {
186 if(deep[top[x]]<deep[top[y]])
187 {
188 swap(x,y);
189 }
190 jia(dfsx[top[x]],dfsx[x],c,rt1);
191 x=father[top[x]];
192 }
193 if(dfsx[x]>dfsx[y])
194 {
195 swap(x,y);
196 }
197 jia(dfsx[x],dfsx[y],c,rt1);
198 }
199
200 int main()
201 {
202 scanf("%d %d %d %d",&n,&m,&r,&mod);
203 //cin>>n>>m>>r>>mod;
204 for(int i=1;i<=n;i++)
205 {
206 scanf("%d",&value[i]);
207 //cin>>value[i];
208 }
209 for(int i=1;i<=n-1;i++)
210 {
211 int a,b;
212 scanf("%d %d",&a,&b);
213 //cin>>a>>b;
214 add(a,b);
215 add(b,a);
216 }
217 tot=0;
218 dfs1(r);
219 dfs2(r,r);
220 tot=0;
221 build(1,n,rt1=tot++);
222 for(int i=1;i<=m;i++)
223 {
224 int flag;
225 int x,y,z;
226 scanf("%d",&flag);
227 //cin>>flag;
228 if(flag==1)
229 {
230 scanf("%d %d %d",&x,&y,&z);
231 //cin>>x>>y>>z;
232 jias(x,y,z);
233 }
234 else
235 if(flag==2)
236 {
237 scanf("%d %d",&x,&y);
238 //cin>>x>>y;
239 int ans;
240 ans=ask(x,y);
241 printf("%d\n",ans);
242 //cout<<ans<<endl;
243 }
244 else
245 if(flag==3)
246 {
247 scanf("%d %d",&x,&y);
248 //cin>>x>>y;
249 jia(dfsx[x],dfsx[x]+size[x]-1,y,rt1);
250 }
251 else
252 if(flag==4)
253 {
254 scanf("%d",&x);
255 //cin>>x;
256 int ans=he(dfsx[x],dfsx[x]+size[x]-1,rt1);
257 printf("%d\n",ans);
258 //cout<<ans<<endl;
259 }
260 }
261 return 0;
262 }
有关例题:
P2146 [NOI2015]软件包管理器


