UVA12169 不爽的裁判 Disgruntled Judge（扩展欧几里得+枚举）

题目链接

题意：

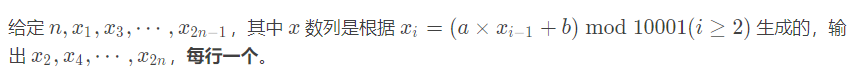
思路：由于n和mod很小，因此可以直接枚举a  -  [0,10000]，然后因为f[3]-a²*f[1]=b*(a+1)用扩展欧几里得求a+1关于MOD的逆元的然后求出b，再去确认ab是否符合。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN = 100+10;
ll f[MAXN];
const int MOD = 10001;
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b)
    {
        x=1;
        y=0;
        return a;
    }
    ll res=exgcd(b,a%b,x,y);
    ll tmp=x;
    x=y;
    y=tmp-(a/b)*y;
    return res;
}
int main()
{
    int n;
    scanf("%d",&n);
    n*=2;
    for(int i=1;i<=n;i+=2)
    {
        scanf("%lld",&f[i]);
    }
    for(int i=0;i<=10000;i++)
    {
        ll a=i;
        ll c=f[3]-a*a*f[1];
        ll b,t;
        ll d=exgcd(a+1,MOD,b,t);
        if(c%d)
        continue;
        b=b*c/d;
        int j;
        for(j=2;j<=n;j++)
        {
            if(j&1)
            {
                if(f[j]!=(a*f[j-1]+b)%MOD)    
                break;
            }
            else
                f[j]=(a*f[j-1]+b)%MOD;
        }
        if(j>n)
            break; 
    }
    for(int i=2;i<=n;i+=2)
    {
        printf("%lld\n",f[i]);
    }
}