查找
0PTA得分截图

1.本周学习总结(0-4分)
1.1 总结查找内容
1.1.1查找的性能指标->ASL(Average Search Length)
1.1.1.1ASL的功能
- 称为关键字的平均比较次数,也称平均搜索长度
- 用一个确定的数值来判断相应查找方法的查找效率(ASL越小,表明效率越高;ASL越大,表明效率越低)
1.1.1.2ASL的计算
- 查找失败的ASL
查找失败目标的查找次数总和/查找失败目标的个数 - 查找成功的ASL
查找成功目标的查找次数综合/查找成功目标的个数
1.1.2静态查找(仅作查询和检索操作的查找表)
1.1.2.1顺序查找
相关概念:
假设有一个表格按顺序存放数据,此时想要在表中查找数据X,方法为:从表的起点按顺序遍历表,直到找到X或者遍历完毕都未找到
举例
- 存在下图数组存储关键字

- 查找关键字2和8

- 代码
int Search(int a[],int n,int X)
{
int i;
for(i=0;i<n;i++) //从头到尾扫描关键字表
{
if(a[i]==X)
{
return i; //成功则返回逻辑序号
}
}
return -1; //标志查找失败
}
- 计算成功与不成功的ASL
成功的ASL:关键字5需要查找1次,关键字7需要查找2次,以此类推...
ASL=1+2+3+4+5+6+7/7=4
不成功的ASL:不管关键字为何值,只要其查找失败,都需要遍历关键字表,查找次数为数组长度
ASL=7
注:对于同一个顺序表来说,查找的ASL不变(成功的ASL为(n+1)/2,失败的ASL为n)
1.1.2.2二分查找
相关概念
举例
-
存在一组关键字

-
在其中查找关键字25,流程如下

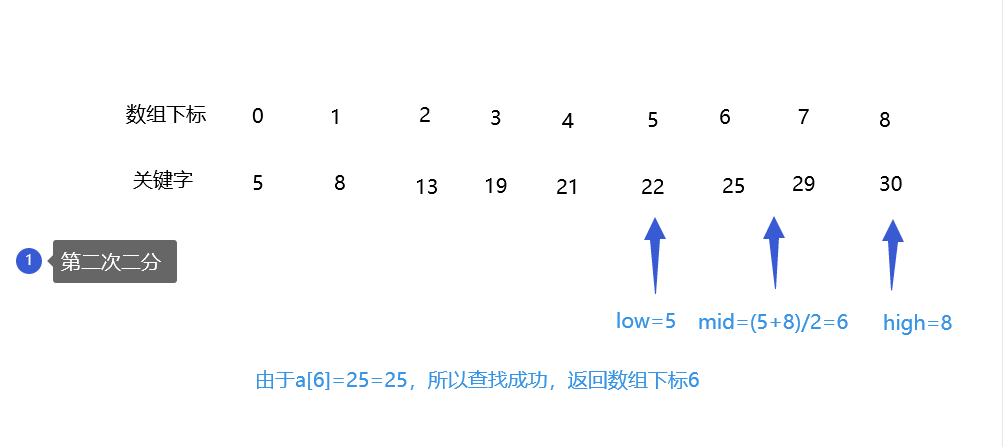
-
代码(分为递归法和非递归法)
非递归法
int Search(int a[],int n,keytype X)
{
int low=0;
int high=n-1;
int mid;
while(low<=high)
{
mid=(low+high)/2;
if(a[mid].key<X)
{
low=mid+1;
}
else if(a[mid].key>X)
{
high=mid-1;
}
else
{
return mid; //查找成功返回逻辑序号
}
}
return -1; //标志着查找失败
}
递归法
int Search(int a[],keytype X,int high,int low)
{
int mid;
if(low<=high)
{
mid=(low+high)/2;
if(a[mid].key>X)
{
return Search(a[],X,mid-1,low);
}
else if(a[mid].key<X)
{
return Search(a[],X,low,mid+1);
}
else
{
return mid;
}
}
else
{
return -1;
}
}
1.1.3动态查找(进行查找操作后,可插入不存在结果或删除存在结果)
1.1.3.1二叉搜索树
定义
-
其可以为空树
-
若其不为空树,则满足以下条件:
(1)非空左子树的所有键值小于其根结点的键值。
(2)非空右子树的所有键值大于其根结点的键值。
(3)左、右子树都是二叉搜索树。
构建: -
构建时步骤
(1)若二叉搜索树为空,则将待插入数据X作为根结点
(2)若待插入数据X和当前结点关键字相同,则无需操作
(3)若待插入数据X大于当前结点的关键字,则插入其右子树
(4)若待插入数据X小于当前结点的关键字,则插入其左子树 -
存在以下一组数据

-
流程图
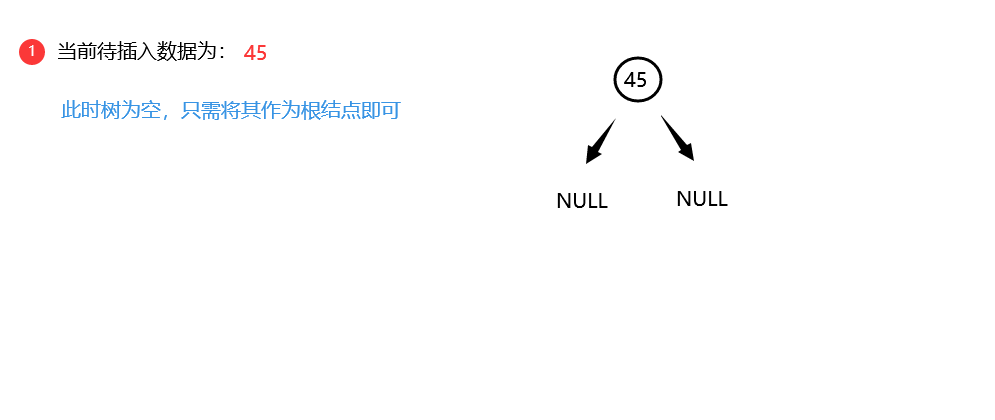
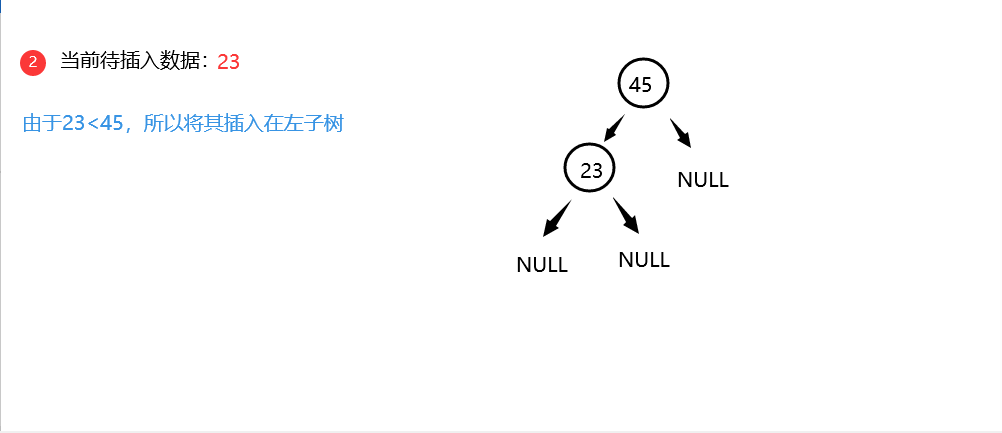
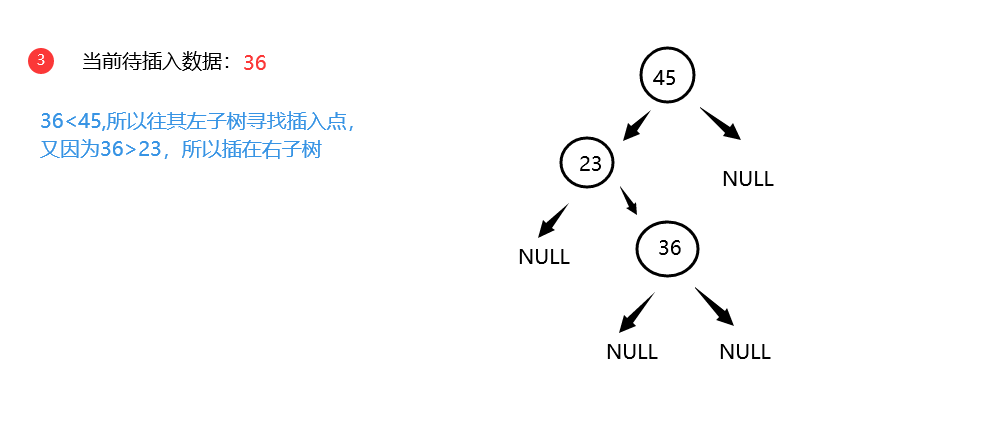
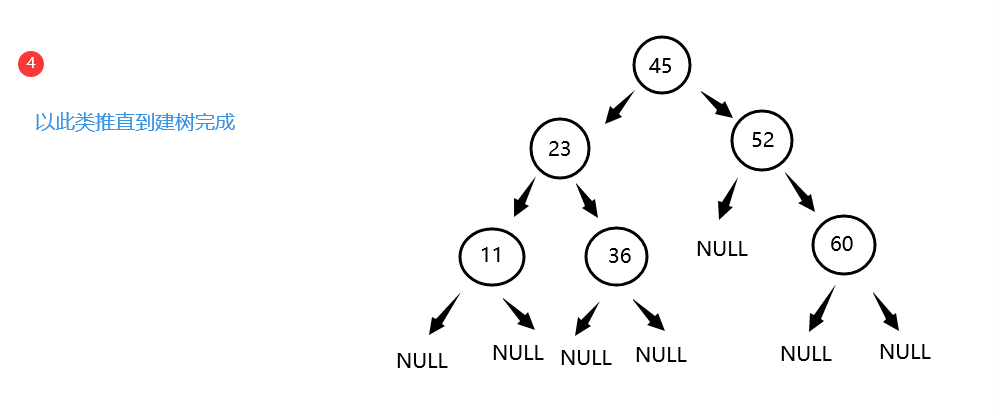
-
代码
void Insert(BinTree &BST,KeyType X)
{
if(BST==BULL) //插入位置在叶节点
{
BST=new BinNode;
BST->key=X;
BST->Left=BST->right=NULL;
}
else
{
if(X>BST->key)
{
Insert(BST->Right,X);
}
else if(X<BST->key)
{
Insert(BST->Left,X);
}
else //已有关键字
{
}
}
}
- 不同的次序生成不同的二叉搜索树
将上述的数据从小到大排序,生成二叉搜索树
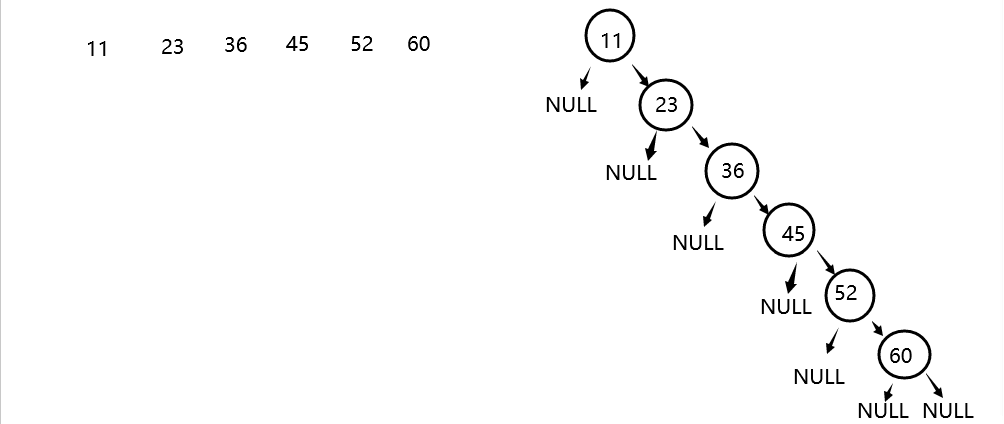
删除:
- 删除时步骤
(1)被删节点为叶子节点
直接删除,置为NULL
(2)被删节点只有左子树或者右子树
用其左孩子代替或者右孩子代替
(3)被删节点同时存在左右子树
有两种解决方案:其一是用其左子树中的最大关键字代替,并且将该最大关键字本身删除;
其二是用其右子树中最小关键字代替,并且将该最小关键字本身删除; - 代码(删除函数)
BinTree Delete(BinTree BST, ElementType X)
{
BinTree temp;
if (BST == NULL)
{
printf("Not Found\n"); }
else
{
if (X < BST->Data)
{
BST->Left = Delete(BST->Left, X);
}
else if (X > BST->Data)
{
BST->Right = Delete(BST->Right, X);
}
else //找到所删点;
{
if (BST->Left && BST->Right) //存在左右孩子
{
BST->Data = FindMax(BST->Left)->Data;
BST->Left = Delete(BST->Left, BST->Data);
}
else
{
if (!BST->Left && !BST->Right)///左右都无
{
free(BST);
}
else
{
if (BST->Left != NULL && BST->Right == NULL) //有左无右
{
temp = BST;
BST = BST->Left;
free(temp);
}
else //有右无左
{
temp = BST;
BST = BST->Right;
free(temp);
}
}
}
}
}
return BST;
}
查找
- 相关知识点
首先从二叉搜索树的根结点开始进行查找,若所找关键字大于当前扫描的树节点关键字,则进入其右孩子,进行比较,若所找关键字小于当前扫描的树节点关键字,则进入其左孩子,进行比较,直到扫描到关键字和所查关键字相同。若在找到关键字之前,扫描到NULL,则说明查找失败,书中无此关键字。 - 代码
bool Find(BinTree BST, int X)
{
if (BST == NULL) //说明未找到,即查找失败
{
return false;
}
else
{
if (X > BST->Data) //进入右孩子
{
return Find(BST->Right, X);
}
else if(X<BST->Data) //进入左孩子
{
return Find(BST->Left, X);
}
else //找到
{
return true;
}
}
}
ASL的计算
1.1.4AVL树(平衡二叉树)
1.1.4.1AVL的定义
- 存在意义

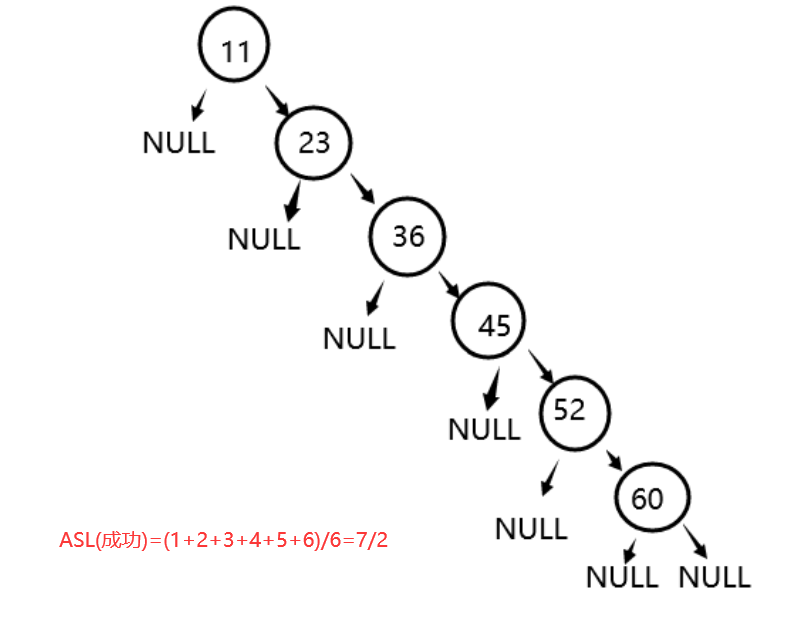
如上图:
(1)对于一组相同的数据,构建的二叉搜索树不同,会导致其ASL不同,即查找效率不同。
(2)进一步观察发现,构建的二叉搜索树形态上越接近完全二叉树,其ASL越低,查找效率越高。 - 相关定义
AVL树(平衡二叉树)任何一个节点的左右子树的深度只差只能取-1,0,1,即0<=|Hr-Hl|<=1。
1.1.4.2四种调整
- 四种调整图示
LL调整
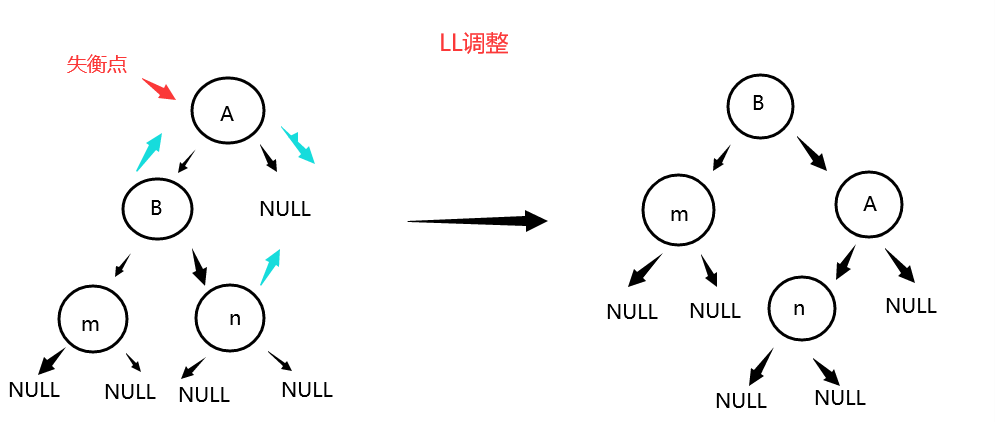
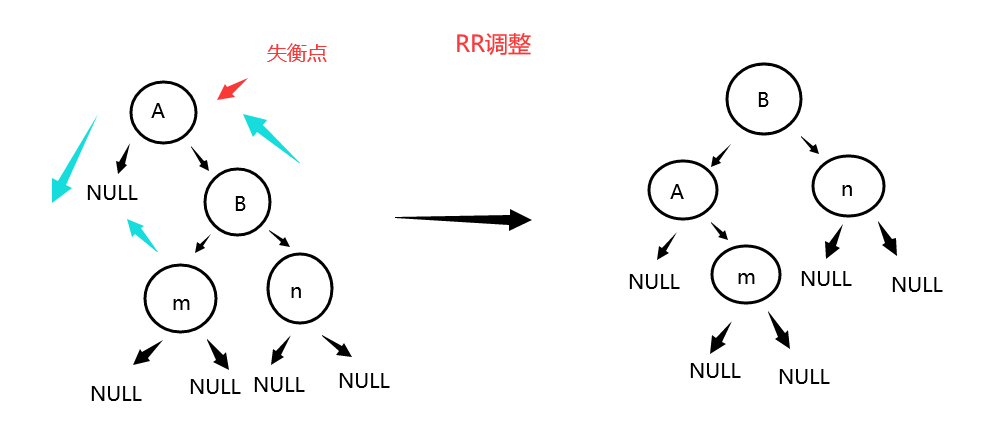
RR调整
LR调整

RL调整
1.1.5B树
1.1.5.1B-树和B+树定义
1.1.5.2B-树的插入
1.1.5.3B-树的删除
1.1.6散列查找
1.1.6.1哈希表
1.1.6.2哈希链
1.2学习体会
2.PTA题目介绍(0--6分)
2.1 题目1(2分)
2.1.1 该题的设计思路
题面分析。分析题面数据如何表达。
文字+图方式介绍解法。如完全二叉树特点、二叉搜索树特点,如何结合解决本题。。。。
计算代码的时间复杂度。
2.1.2 该题的伪代码
文字+代码简要介绍本题思路
2.1.3 PTA提交列表
提交列表截图。并介绍代码编写中碰到问题及解决方法。




