缩小图像（或称为下采样（subsampled）或降采样（downsampled））的主要目的有两个：1、使得图像符合显示区域的大小；2、生成对应图像的缩略图。当缩减像素取样（减少像素的数量）时，将从图像中删除一些信息图像的质量将不可避免地受到影响。然而，确实有一些缩放方法能够增加图像的信息，从而使得缩放后的图像质量超过原图质量的。
放大图像（或称为上采样（upsampling）或图像插值（interpolating））的主要目的是放大原图像,从而可以显示在更高分辨率的显示设备上。当向上重新取样（增加像素的数量或增加像素取样）时，将添加新的像素。可以指定插值算法来确定如何添加或删除像素。
插值就是在不生成像素的情况下增加图像像素大小的一种方法，根据周围像素色彩使用数学方法计算丢失像素的色彩，插值并不能增加图像信息。
插值算法分类
1.传统差值原理和评价
在传统图像插值算法中，邻插值较简单，容易实现，早期的时候应用比较普遍。但是，该方法会在新图像中产生明显的锯齿边缘和马赛克现象。双线性插值法具有平滑功能，能有效地克服邻法的不足，但会退化图像的高频部分，使图像细节变模糊。在放大倍数比较高时，高阶插值，如双三次和三次样条插值等比低阶插值效果好。这些插值算法可以使插值生成的像素灰度值延续原图像灰度变化的连续性，从而使放大图像浓淡变化自然平滑。但是在图像中，有些像素与相邻像素间灰度值存在突变，即存在灰度不连续性。这些具有灰度值突变的像素就是图像中描述对象的轮廓或纹理图像的边缘像素。在图像放大中，对这些具有不连续灰度特性的像素，如果采用常规的插值算法生成新增加的像素，势必会使放大图像的轮廓和纹理模糊，降低图像质量。
2.基于边缘的图像插值算法
为了克服传统方法的不足， 提出了许多边缘保护的插值方法，对插值图像的边缘有一定的增强， 使得图像的视觉效果更好， 边缘保护的插值方法可以分为两类： 基于原始低分辨图像边缘的方法和基于插值后高分辨率图像边缘的方法。基于原始低分辨率图像边缘的方法:( 1)首先检测低分辨率图像的边缘， 然后根据检测的边缘将像素分类处理， 对于平坦区域的像素，采用传统方法插值；对于边缘区域的像素， 设计特殊插值方法， 以达到保持边缘细节的目的。(2)基于插值后高分辨率图像边缘的方法这类插值方法:首先采用传统方法插值低分辨率图像，然后检测高分辨率图像的边缘，最后对边缘及附近像素进行特殊处理， 以去除模糊， 增强图像的边缘。
3.基于区域的图像插值算法
首先将原始低分辨率图像分割成不同区域，然后将插值点映射到低分辨率图像， 判断其所属区域， 最后根据插值点的邻域像素设计不同的插值公式， 计算插值点的值。
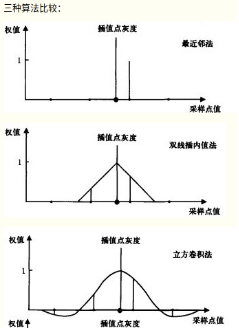
下面介绍三种传统插值算法：最近邻插值、双线性插值、双立方插值
1. 最近相邻插值算法(Nearest Neighbour Interpolation)
取待采样点周围4个相邻像素点中距离最近的 1个邻点的灰度值作为该点的灰度值。
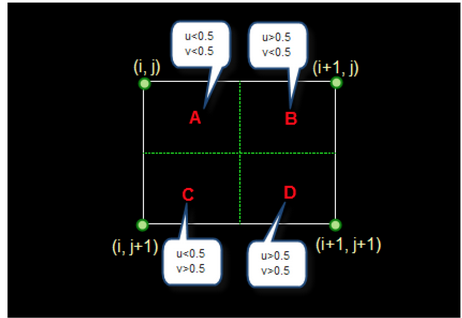
如果 i+u, j+v(i落在 A区，即 u<0.5,v<0.5，则将左上角象素的灰度值赋给待求象素，同理落在B区则赋予右上角的象素灰度值，落在C区则赋予左下角象素的灰度值，落在D区则赋予右下角象素的灰度值。
最近邻插值法计算量较小，但可能会造成生的图像灰度上的不连续，在变化地方可能出现明显锯齿状。
优点：算法简单，运算速度较快。
缺点：仅使用离待测采样点最近的像素的灰度值作为该采样点的灰度值，而没考虑其他相邻像素点的影响，因而重新采样后灰度值有明显的不连续性，图像质量损失较大，会产生明显的马赛克和锯齿现象。
2.双线性插值算法(Bilinear Interpolation)
线性插值法是指使用连接两个已知量的直线来确定在这个两个已知量之间的一个未知量的值的方法。 双线性插值是插值算法中的一种，是线性插值的扩展。利用原图像中目标点四周的四个真实存在的像素值来共同决定目标图中的一个像素值，其核心思想是在两个方向分别进行一次线性插值。
https://www.cnblogs.com/kk17/p/9989984.html
假设源图像大小为mxn，目标图像为axb。那么两幅图像的边长比分别为：m/a和n/b。注意，通常这个比例不是整数，编程存储的时候要用浮点型。目标图像的第（i,j）个像素点（i行j列）可以通过边长比对应回源图像。其对应坐标为（i*m/a,j*n/b）。显然，这个对应坐标一般来说不是整数，而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值（灰度值或者RGB值）。
若图像为灰度图像，那么（i，j）点的灰度值的数学计算模型是：
f(x,y)=b1+b2x+b3y+b4xy
其中b1,b2,b3,b4是相关的系数。关于其的计算过程如下如下：
如图，已知Q12，Q22，Q11，Q21，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对R1和R2两个点进行插值，这个很简单，然后根据R1和R2对P点进行插值，这就是所谓的双线性插值。
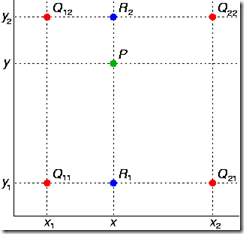
双线性插值，又称为双线性内插。在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。
假如我们想得到未知函数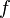
在点 
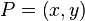的值，假设我们已知函数
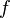在
, 
, 
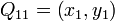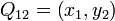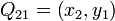, 及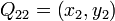 
四个点的值。
首先在 x 方向进行线性插值，得到
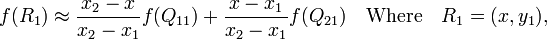
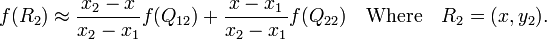
然后在 y 方向进行线性插值，得到
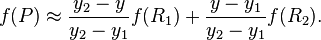
这样就得到所要的结果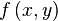 
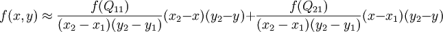
如果选择一个坐标系统使得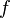
的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为
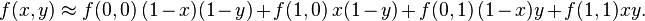
或者用矩阵运算表示为
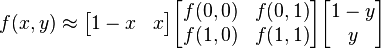
这种插值方法的结果通常不是线性的，线性插值的结果与插值的顺序无关。首先进行 y 方向的插值，然后进行 x 方向的插值，所得到的结果是一样的。
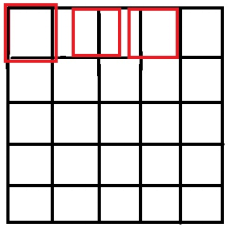
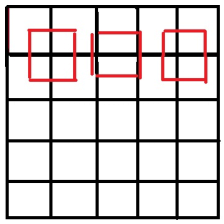
在坐标系的选择方面，如果选择右上角为原点（0，0），那么最右边和最下边的像素实际上并没有参与计算，而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上如下左图所示。
在matlab和openCV中的双线性插值过程，会将目标图和原图的几何中心重合，并且目标图像的每个像素之间都是等间隔的和两边有一定的边距，使得源图像和目标图像各个像素之间的对应关系如下右图：
优点：输出的图像的每个像素都是原图中四个像素(2×2)运算的结果，由于它是从原图四个像素中运算的，因此这种算法很大程度上消除了锯齿现象，而且效果也比较好。
缺点：此方法仅考虑待测样点周围四个直接邻点灰度值的影响, 而未考虑到各邻点间灰度值变化率的影响, 因此具有低通滤波器的性质, 从而导致缩放后图像的高频分量受到损失, 图像边缘在一定程度上变得较为模糊。用此方法缩放后的图像与原图像相比，仍然存在由于计算模型考虑不周而产生的图像质量退化与精度降低的问题。
3.双三次插值算法
双三次插值算法(Bicubic Interpolation)是两次线性插值算法的改进算法，“不仅考虑到四个直接邻点灰度值的影响，还考虑到各邻点间灰度值变化率的影响”，利用了待采样点周围更大邻域内像素的灰度值作三次插值。
该算法考虑了待求像素坐标反变换后得到的浮点坐标周围的16个邻近像素。目的坐标M(x,y)和浮点坐标m(i+u,j+v)，需要选取插值基函数来拟合数据，常用的插值基函数是对sin[(π*x)/x]的逼近,利用三次多项式S(x)求逼近理论上最佳插值函数sin[(π*x)/x]
插值公式为：
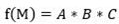
设原始灰度图矩阵为Im,其中矩阵B又为：
B = Im[i-1,i+2,j-1,j+2]
k=0时即为双线性内插法，因此可把双三次插值算法看成由两部分组成，其中（1—|u|）代表直接邻点间灰度值对待采样点的影响，而k则代表邻点间灰度值的变化率对待采样点的影响。
优点：不仅考虑了直接邻点的灰度值还考虑了邻点间灰度值变化率的影响，因此后者所求得的待采样点灰度值更接近原（采样）值。
缺点：计算量最大，算法最为复杂，此方法用进一步增大计算量来换取待采样点精度的进一步提高
参考：
https://blog.csdn.net/majinlei121/article/details/46742339
https://blog.csdn.net/TianxiaoV/article/details/51112989
https://www.cnblogs.com/wjgaas/p/3597095.html
