递归（一）

学习资源程序设计与算法（二）算法基础_北京大学_中国大学MOOC(慕课) (icourse163.org)

递归的基本概念

• 一个函数调用其自身，就是递归
• 求n！的递归函数

 

个人理解：类似于数列的通项公式：a(n)=n*a(n-1);a(1)=1;

递归和普通函数调用一样是通过栈实现的

 

递归的作用

1、代替多重循环

2、解决本来就是用递归形式定义的问题

3、将问题分级为规模更小的子问题进行求解

……

例题：汉诺塔问题

古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上（如图）。有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子 始终保持大盘在下，小盘在上。在移动过程中可以利用B座，要求输出移动 的步骤。

 

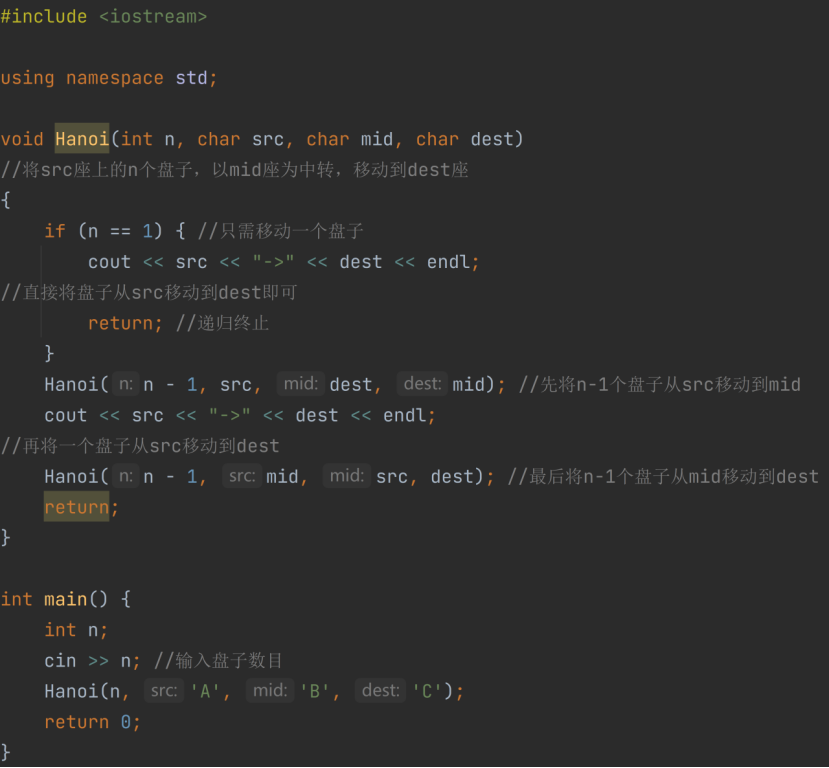
简单版本：

 

 

 

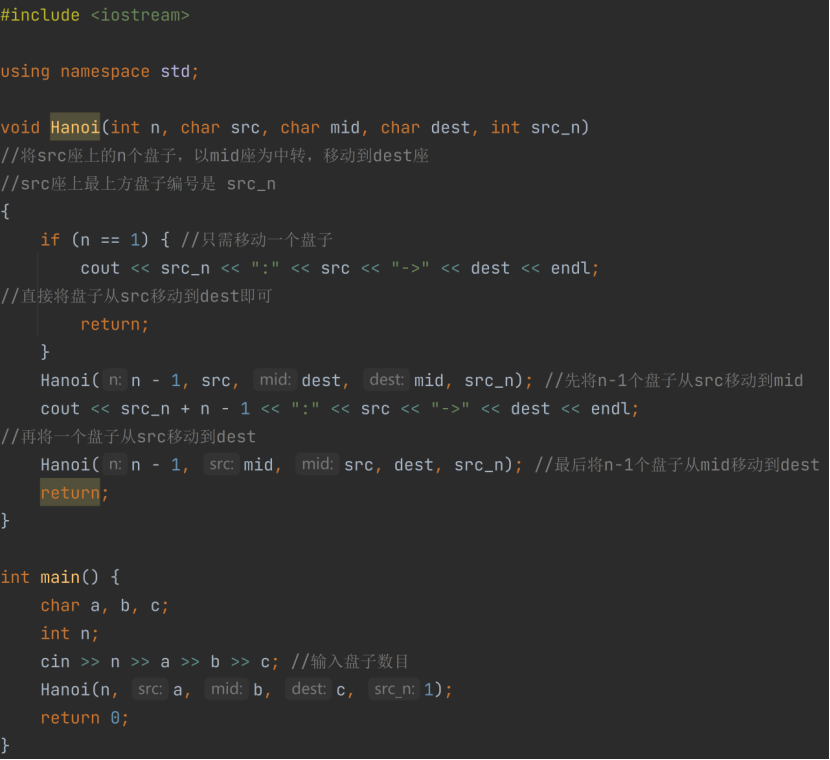
能通过提交的版本：

 

汉诺塔问题手工解法(三个盘子）

 

 

 

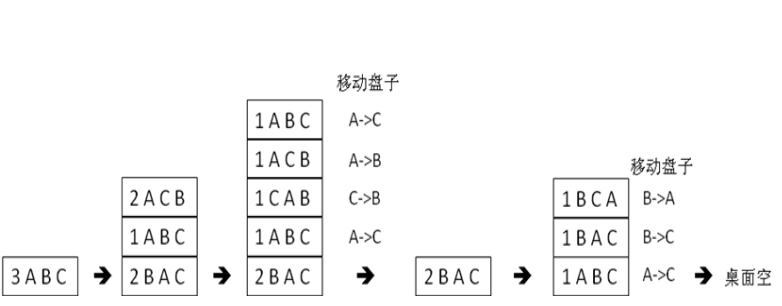
3ABC意思是：有三个盘子需要从A借助B移动到C；其他同理

个人理解：将需要的操作存到栈里面，当只需要将一个盘子移动到另一个桌面时，不需要中转，直接移动，就可以输出操作，代码中src相当于起点，dest相当于终点，mid是媒介；

 

用递归代替多重循环

n皇后问题：输入整数n, 要求n个国际象棋的皇后，摆在 n*n的棋盘上，互相不能攻击，输出全部方案。

八皇后问题：八重循环。n皇后，n重循环？

 

递归解决！

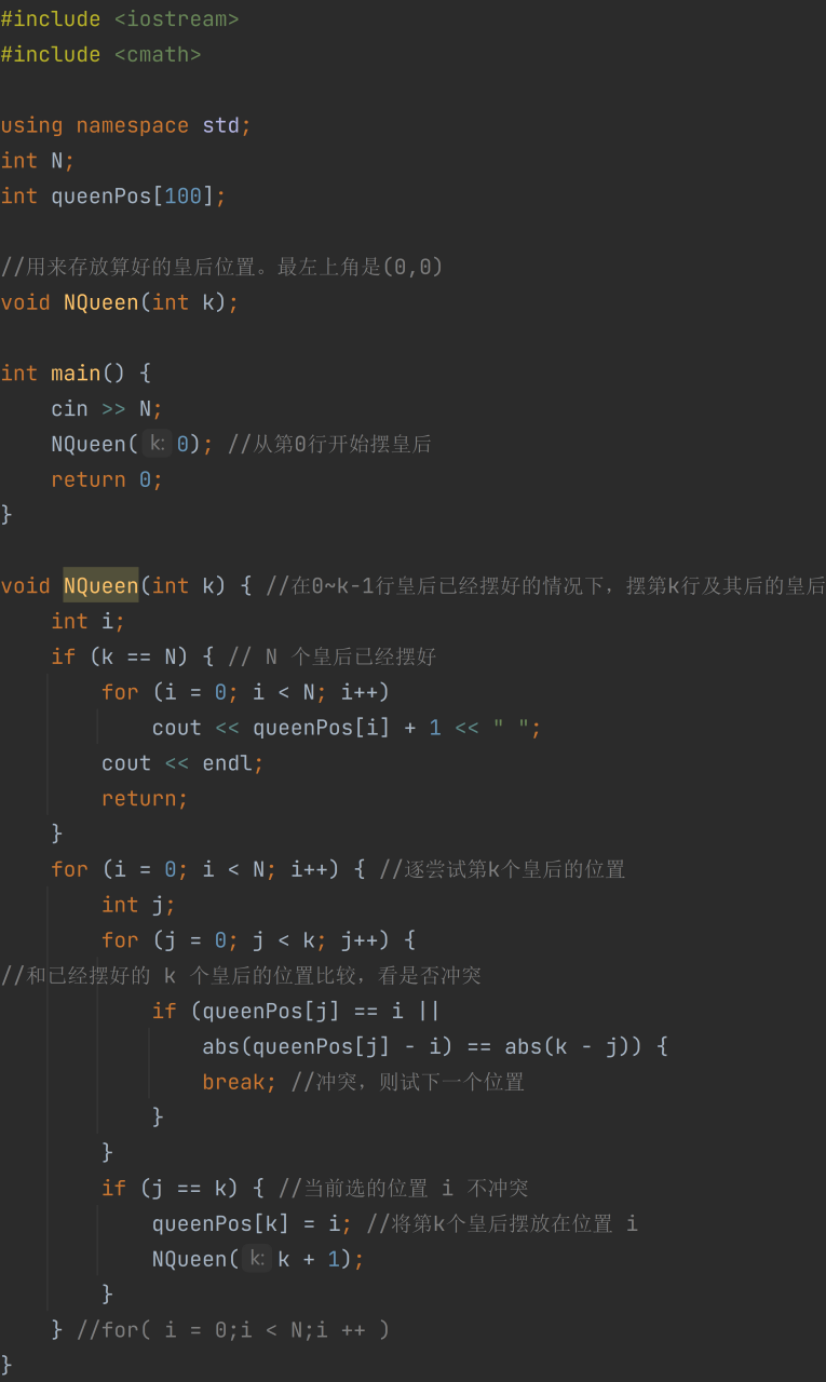
N皇后问题

输入一个正整数N，则程序输出N皇后问题的全部摆法。 输出结果里的每一行都代表一种摆法。行里的第i个数字如果是n，就代表第i行的皇后应该放在第n列。 皇后的行、列编号都是从1开始算。

样例输入：

4

样例输出：

2 4 1 3

3 1 4 2

代码：

 

 

 

逆波兰表达式

用递归解决递归形式的问题

例题：逆波兰表达式

逆波兰表达式是一种把运算符前置的算术表达式(其实一般教科书上称这种表 达式为波兰表达式） ，例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰 表达式的优点是运算符之间不必有优先级关系，也不必用括号改变运算次序，例如 (2 + 3) * 4的逆波兰表示法为* + 2 3 4。本题求解逆波兰表达式的值，其中运算符 包括+ - * /四个。

输入

输入为一行，其中运算符和运算数之间都用空格分隔，运算数是浮点数

输出

输出为一行，表达式的值。

样例输入

* + 11.0 12.0 + 24.0 35.0

样例输出

1357.000000

提示：(11.0+12.0)*(24.0+35.0)

本题中“逆波兰表达式”的定义：

1) 一个数是一个逆波兰表达式，值为该数

2)  "运算符 逆波兰表达式 逆波兰表达式" 是逆波兰表达 式 ，值为两个逆波兰表达式的值运算的结果

一般教科书将本题中的“逆波兰表达式”称为“波兰表达式”，而将运 算符后置的表达式成为“逆波兰表达式”

 

代码如下：

 

 

 

atof() 函数

C 标准库 - <stdlib.h>

描述

C 库函数 double atof(const char *str) 把参数 str 所指向的字符串转换为一个浮点数（类型为 double 型）。

下面是 atof() 函数的声明。

double atof(const char *str)

参数

str -- 要转换为浮点数的字符串。

返回值

函数返回转换后的双精度浮点数，如果没有执行有效的转换，则返回零（0.0）。