机器人单关节力矩控制
对于自由运动机器人来说,控制的目的是要控制机器人末端的位置和姿态(统一简称为位置),即所谓的位置控制问题。期望机器人末端达到的位置称为期望位置或期望轨迹,期望轨迹可以在机器人任务空间中给出,也可以通过逆运动学转化为机器人关节空间中的期望轨迹。期望轨迹通常有两种形式:一种是一个固定位置(setpoint),另一种是一条随时间连续变化的轨迹(trajectory)。
对于运动受限的机器人来说,其控制问题要复杂得多。由于机器人与环境接触,这时不仅要控制机器人末端位置,还要控制末端作用于环境的力。也就是说,不仅要使机器人末端达到期望值,还要使其作用于环境的力达到期望值。更广泛意义下的运动受限机器人还包括机器人协同工作的情况,这时控制还应包括各机器人间运动的协调,负荷的分配以及所共同夹持的负载所受内力的控制等复杂问题。
如下图所示,考虑单个电机与连杆的模型,其中为电机施加的力矩,是连杆与水平线的夹角:
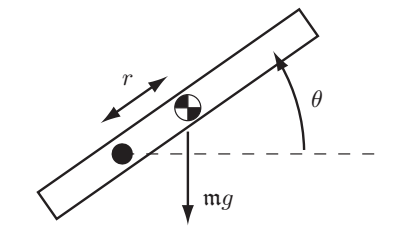
则系统的动力学方程为:
是连杆绕转轴的转动惯量,是连杆的质量,是转轴到连杆质心的距离,是重力加速度。实际情况中转轴处会存在摩擦力,这里简单假设摩擦力为粘滞阻力,即,将阻力项加入上面的动力学方程中,模型变为:
可将其改写为:
为进行仿真,设参数,,,,当连杆在平面上运动时,当连杆垂直水平面运动时
- PID控制
PID控制器时是最常用的反馈控制器。
其中比例系数的作用就像一个虚拟弹簧,试图减小位置误差;微分系数的作用像虚拟阻尼器,试图减小速度误差;积分系数可以减小稳态误差。
- PD控制器与误差的二阶方程
忽略积分项,即,这就是PD控制。我们假设机器人在水平面上运动(g=0),将PD控制规则带入动力学方程中可得到,如果给定的控制量恒定,则,于是,,。动力学方程可改写为误差的二阶微分方程:
将其改写为标准二阶形式:
阻尼比和阻尼自然频率为:、
- PID控制器与误差的三阶方程
考虑连杆在垂直水平面的平面上转动(g>0),用上面的PD控制器,误差动力学方程可写为:
这意味着稳态时满足,即当时最终误差不为零,因为机器人需要提供一个非零的力矩使连杆保持在这个位置。
设,,连杆初始角度,初始角速度,期望角度,期望角速度。根据所设置的参数在Mathematica中求解微分方程,结果如下:
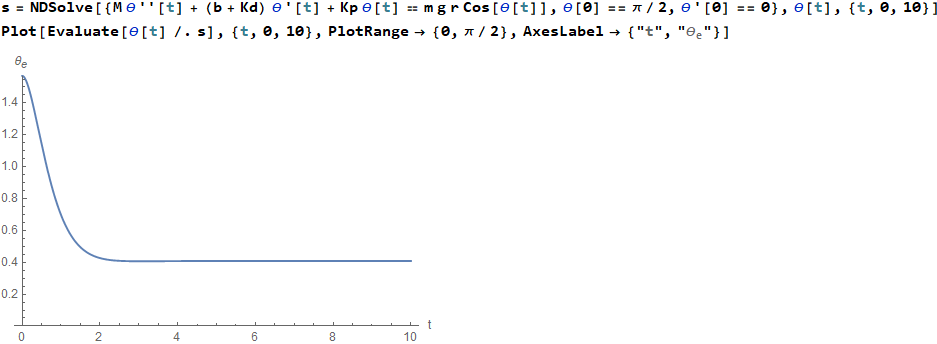
稳态误差可求解方程求得,约为-0.408弧度,即稳态时与期望值相差23.4°
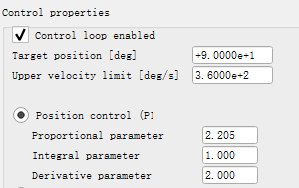
可以在VREP中仿真该过程,新建一个长度为0.2m的圆柱体,质量设为1kg,在圆柱体一段添加旋转关节,圆柱体X、Y轴的转动惯量设为0.49(根据转动惯量的平行轴定理,绕关节转动的转动惯量为0.5)。关节设为力矩模式,打开关节动力学属性对话框,设置PID参数和目标位置(90°):
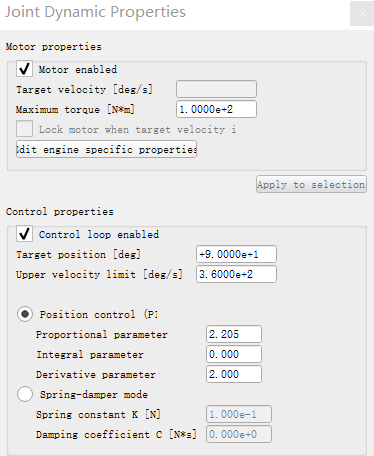
选择ODE物理引擎进行仿真,打开圆柱体动力学属性对话框,点击编辑材料(Edit material),在Angular damping中输入0.1(Angular damping:an angular movement damping value, that adds angular drag, and that can increase stability)。给关节添加阻力可参考Set internal friction of joints和Material properties。
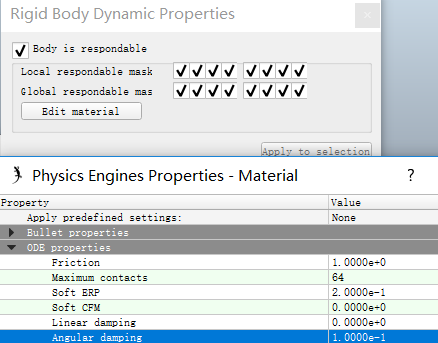
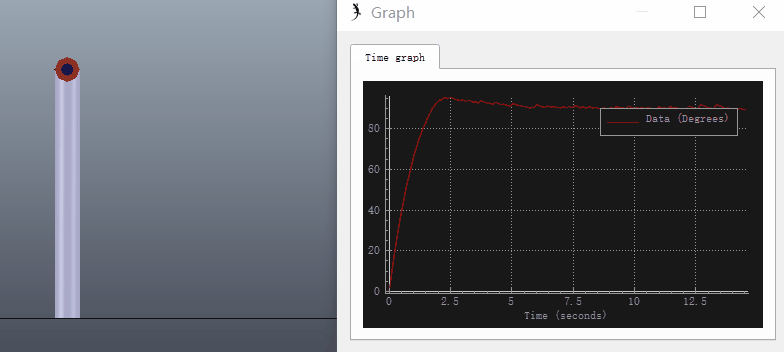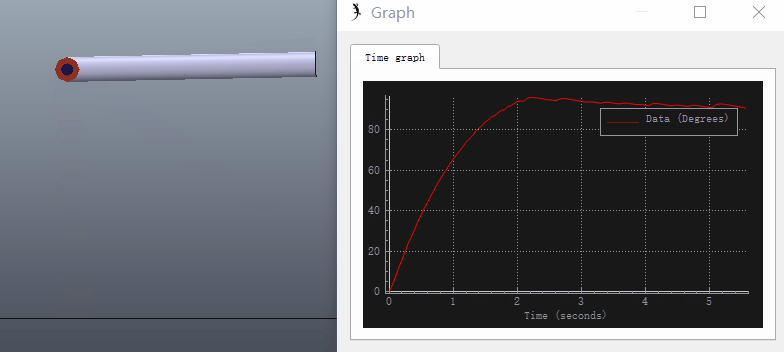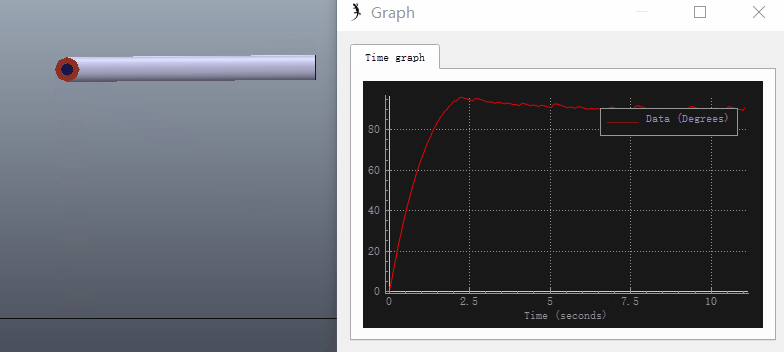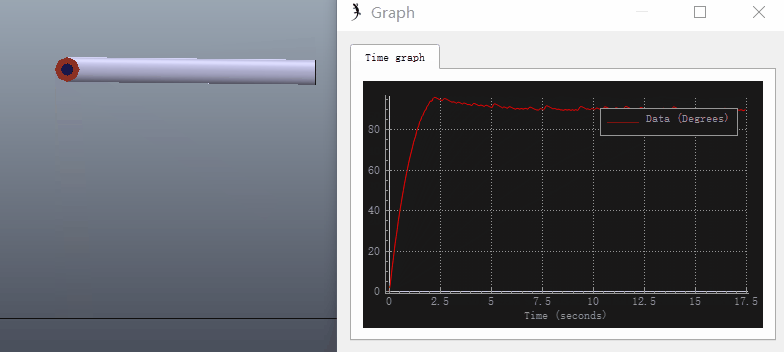
添加Graph记录关节转角进行仿真,可以看出存在稳态误差:
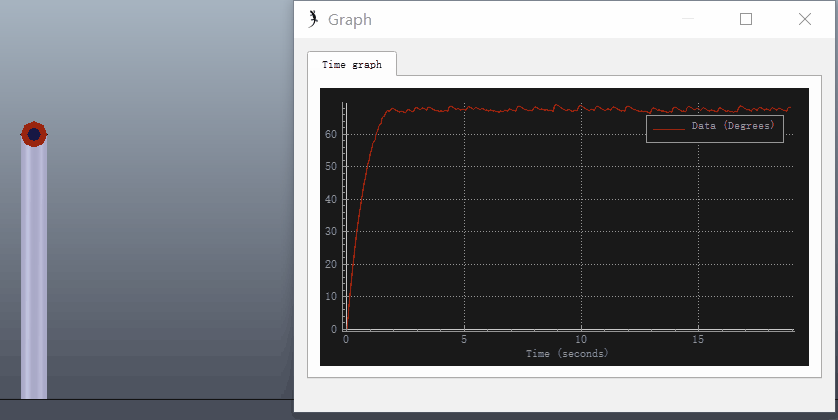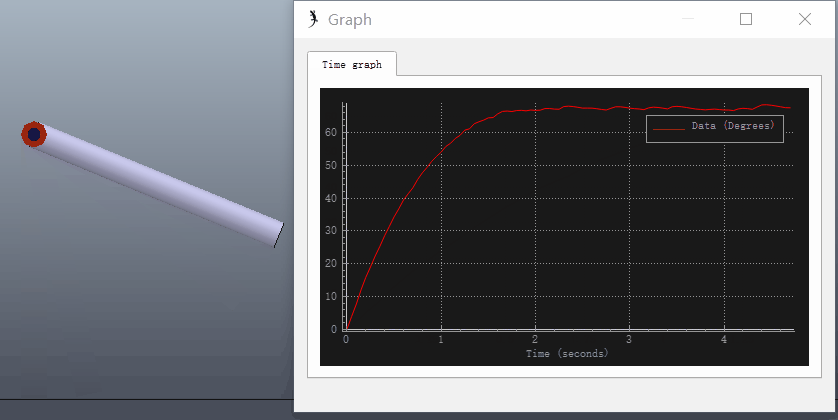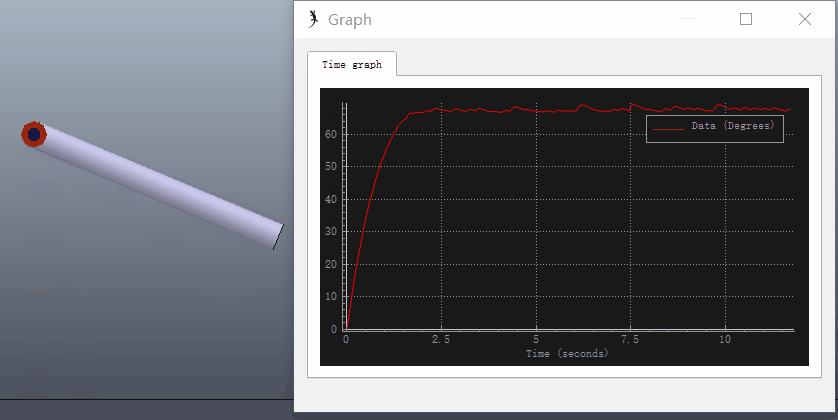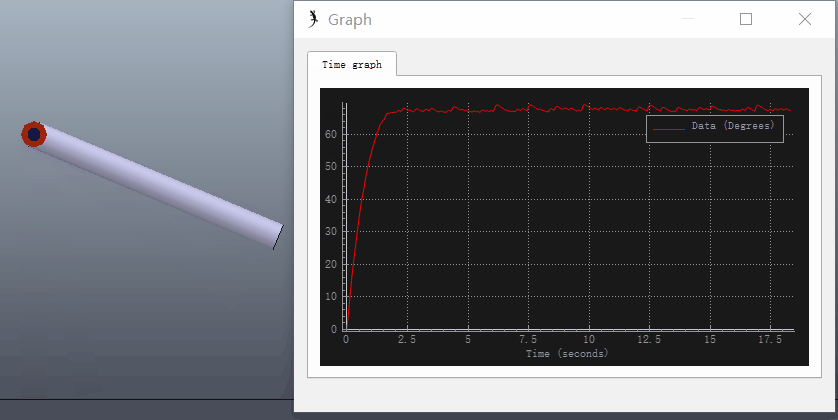
为了消除稳态误差,设,即使用PID控制器。积分控制的作用是消除稳态误差,因为系统只要存在误差,积分作用就不断地积累,输出控制量,直到偏差为零,积分作用才会停止。但积分作用太强会使系统超调加大,甚至使系统出现振荡。加入积分项后关于误差的微分方程为:,其中是重力项。对该方程两边求导,可以得到误差的三阶微分方程:
如果为常量(比如稳态时),方程右边项为零。使用拉普拉斯变换将时域中的微分方程转换为复数域中的代数方程:
如果该特征方程根的实部全为负,则该系统稳定,且趋于零。根据系统特征方程的劳斯判据,为了保证方程所有根的实部都为负,PID控制器的系数必须满足下列条件:
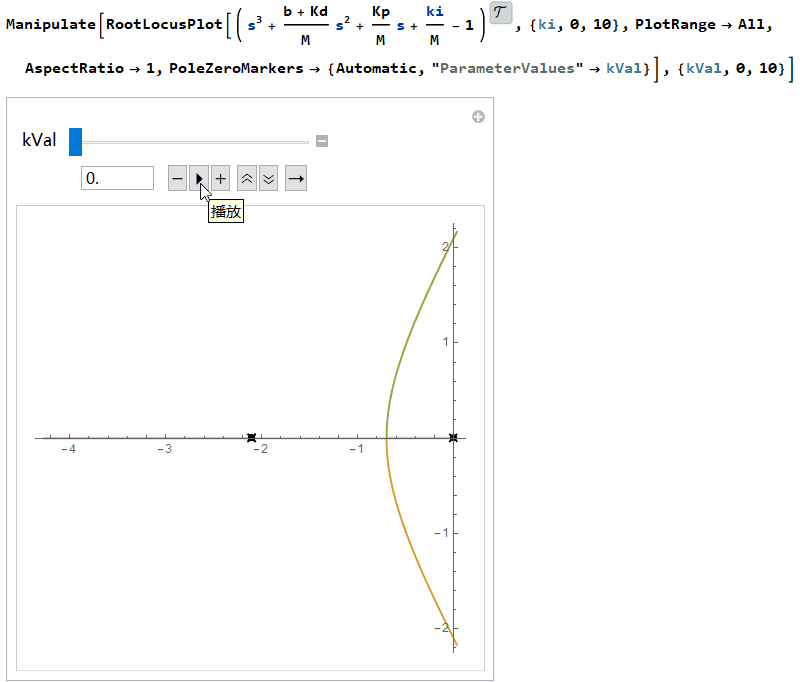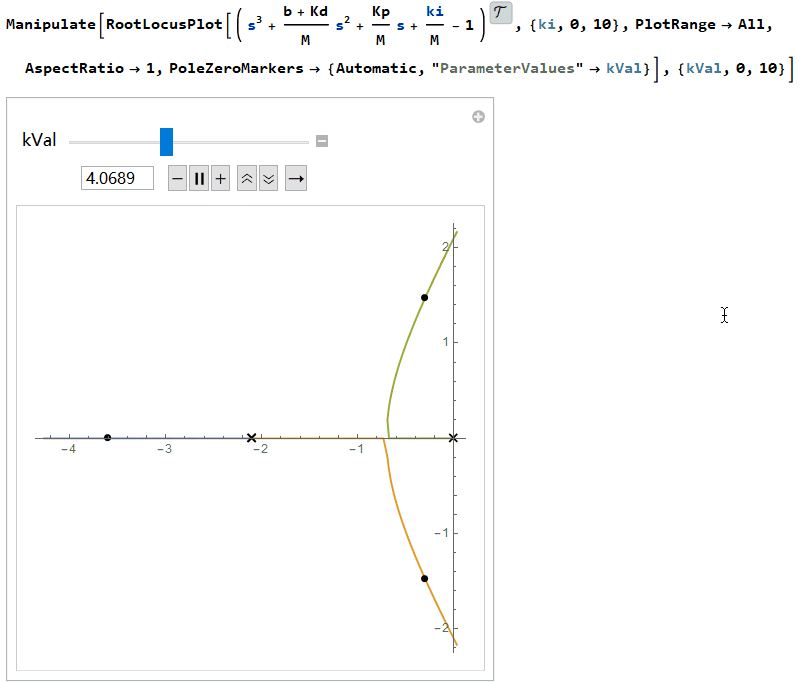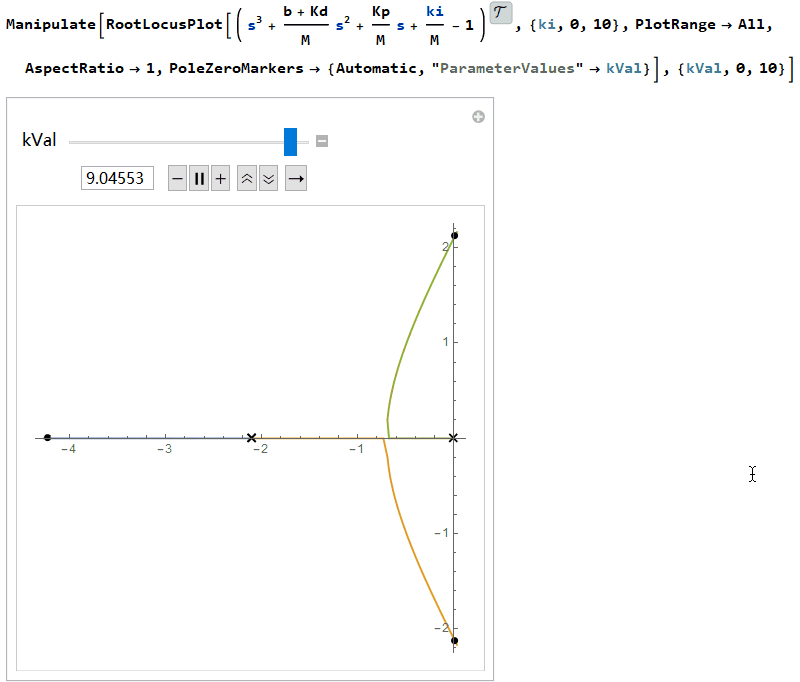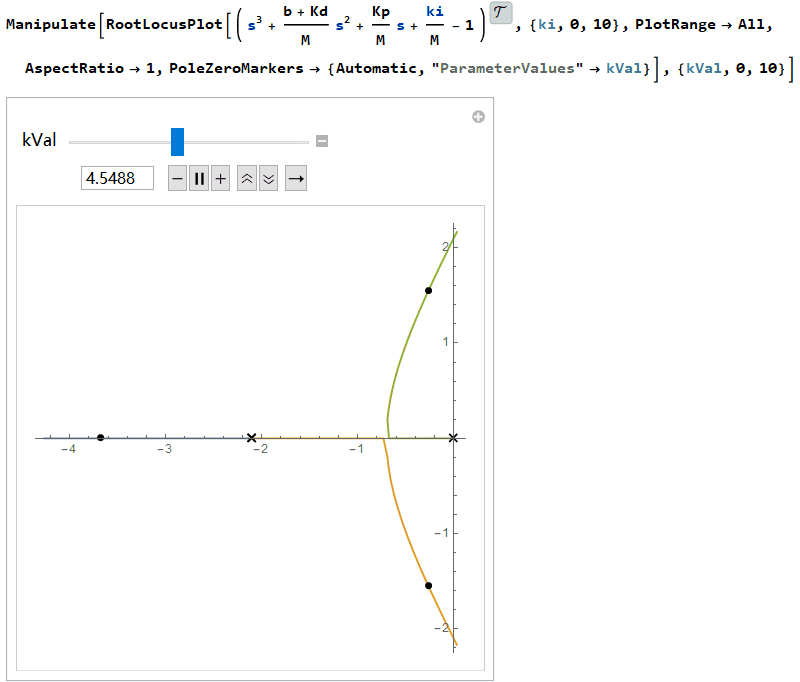
因此的值必须保证落在上下界限之内。通常先选择合适的、值加快暂态过程,然后调整使其能大到消除稳态误差,又不至于过大而影响稳定性。画出根轨迹图(根轨迹是指系统开环传递函数中某个参数从零变到无穷时,闭环特征根s在平面上移动的轨迹),可以看出当时两个根将到达虚轴,继续变大根会进入复平面的右半部分,此时系统将变得不稳定。
PID控制的伪代码如下:
time = 0 // dt = servo cycle time eint = 0 // error integral qprev = senseAngle // initial joint angle q loop [qd,qdotd] = trajectory(time) // from trajectory generator q = senseAngle // sense actual joint angle qdot = (q - qprev)/dt // simple velocity calculation qprev = q e = qd - q edot = qdotd - qdot eint = eint + e*dt tau = Kp*e + Kd*edot + Ki*eint commandTorque(tau) time = time + dt end loop
使用之前建立好的VREP模型,设置积分系数后再进行仿真:
可以看出添加积分项后稳态误差消除(但是产生了超调量):
实际上在许多机器人控制器中设,即不使用积分项。因为相比稳态误差,稳定性才是最重要的考虑因素。
- 前馈控制(Feedforward Control)
PID控制不考虑机器人的动力学特性,只按照偏差进行负反馈控制,即只有在得到误差信号后才能输出控制量。另一种控制策略是根据机器人动力学模型预先产生控制力/力矩。动力学模型为:
根据轨迹生成器输出的期望位置、速度、加速度,前馈力矩为:
前馈控制伪代码如下:
time = 0 // dt = servo cycle time loop [qd,qdotd,qdotdotd] = trajectory(time) // trajectory generator tau = Mtilde(qd)*qdotdotd + htilde(qd,qdotd) // calculate dynamics commandTorque(tau) time = time + dt end loop
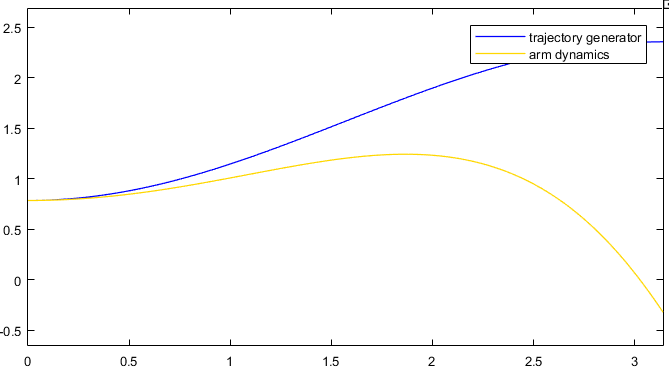
如果动力学模型完全准确,那么用前馈控制即可直接计算力矩。但实际上模型总是存在各种误差,因此前馈控制一般总是与反馈控制结合起来使用。比如下面这个例子,如果,即动力学公式中转轴到质心距离这个参数为0.08m(实际上这个值为0.1m)。因为存在测量和制造误差,准确的动力学模型很难得到。考虑2个任务:任务1连杆运动轨迹为,运动时间为;任务2连杆运动轨迹为,运动时间为
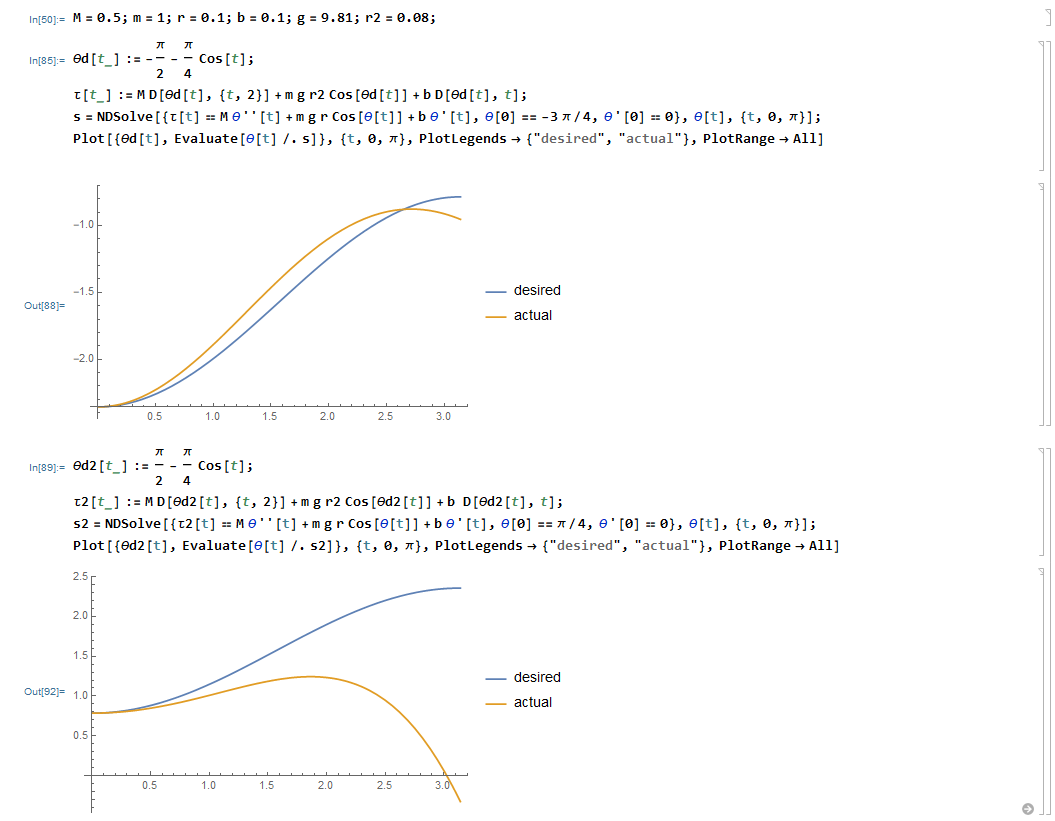
可以看出模型存在误差的情况下,根据动力学方程计算力矩而得到的结果与期望值之间存在偏差。对于任务2重力会阻碍期望的运动,导致产生较大的跟踪误差。
对任务2,在MATLAB/Simulink中进行仿真也可以得到同样的结果:
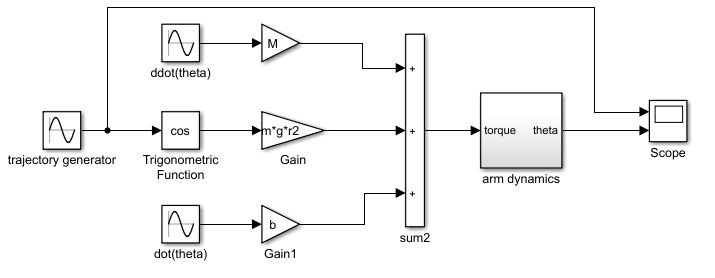
其中arm dynamics子模块根据输入的力矩计算并输出角度或角速度:
期望角度轨迹(蓝线)与根据不准确的动力学模型计算的实际轨迹(橙线)如下图所示:
- 前馈-反馈控制(feedforward and feedback control)
结合前馈与反馈,实际角加速度可写为:
将其带入动力学预测方程中可得到前馈-反馈控制器:
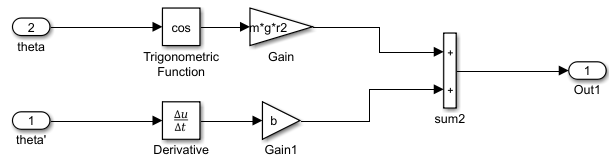
前馈-反馈控制器的结构如下图所示,通常设为零,即使用PD+前馈控制:
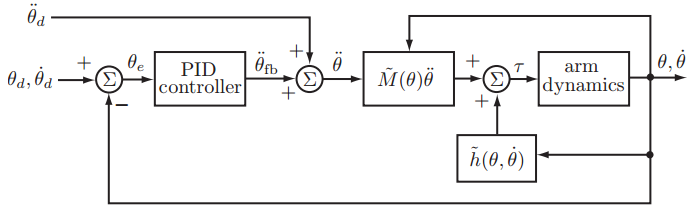
前馈-反馈控制的伪代码如下:
time = 0 // dt = cycle time eint = 0 // error integral qprev = senseAngle // initial joint angle q loop [qd,qdotd,qdotdotd] = trajectory(time) // from trajectory generator q = senseAngle // sense actual joint angle qdot = (q - qprev)/dt // simple velocity calculation qprev = q e = qd - q edot = qdotd - qdot eint = eint + e*dt tau = Mtilde(q)*(qdotdotd+Kp*e+Kd*edot+Ki*eint) + htilde(q,qdot) commandTorque(tau) time = time + dt end loop
单独使用PID控制的Simulink模型如下图所示(参数与任务2中一样):
前馈-反馈控制的模型如下图所示(PID参数与任务2一样):
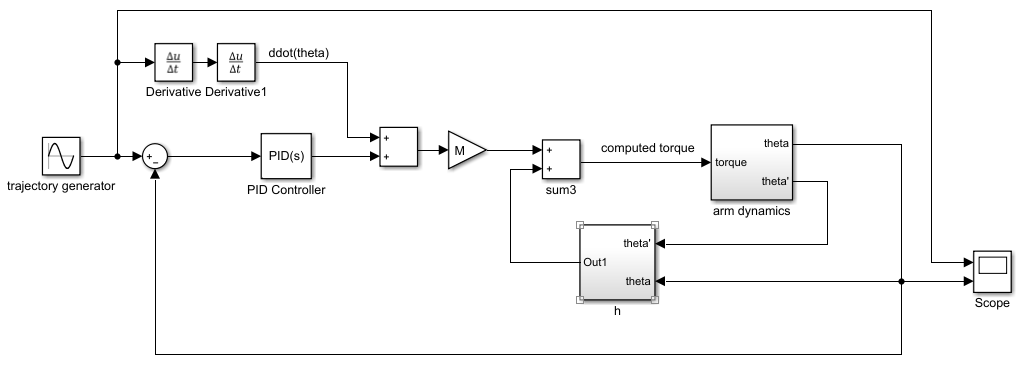
子模块如下图所示:
各控制方法输出的曲线与期望轨迹的对比如下图所示(固定步长0.01s,仿真时间t=pi):
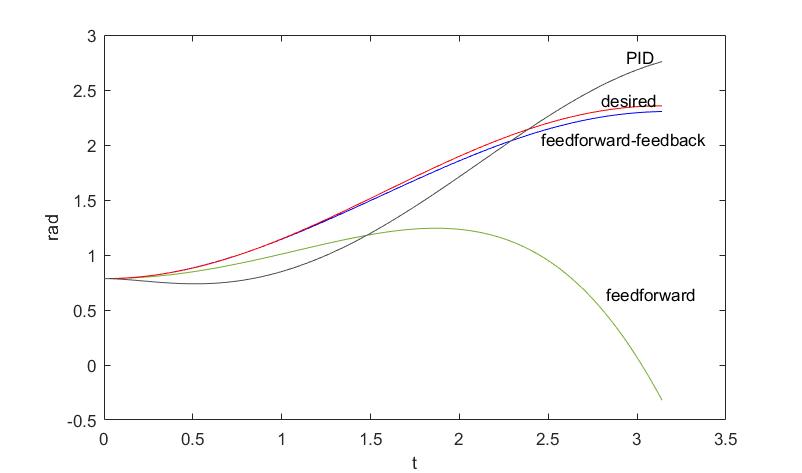
可以看出单独使用前馈控制存在很大跟踪误差,单独使用PID反馈控制对轨迹的跟踪效果也不理想。前馈+反馈控制方案结合了二者的优点,动态跟踪误差最小。
参考:
《机械控制工程基础》
《机器人动力学与控制》 霍伟
Modern Robotics: Mechanics, Planning, and Control Code Library
Modern Robotics Mechanics, Planning, and Control Chapter 11.4 Motion Control with Torque or Force Inputs






【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 浏览器原生「磁吸」效果!Anchor Positioning 锚点定位神器解析
· 没有源码,如何修改代码逻辑?
· 全程不用写代码,我用AI程序员写了一个飞机大战
· DeepSeek 开源周回顾「GitHub 热点速览」
· 记一次.NET内存居高不下排查解决与启示
· MongoDB 8.0这个新功能碉堡了,比商业数据库还牛
· 白话解读 Dapr 1.15:你的「微服务管家」又秀新绝活了