旋转变换的指数形式
用单位向量^ω代表旋转轴,以及θ代表绕该轴的旋转角度。则可以用三维向量^ωθ∈R3以指数形式来描述旋转。如果将^ω和θ分开描述,即为Axis-Angle形式。用^ωθ来描述旋转矩阵R可以有下面几种理解方法:
- 某坐标系初始与参考坐标系{s}重合,绕轴^ω旋转θ角度后当到达当前姿态,其相对于{s}的旋转矩阵为R。这种描述方法为 Axis–angle representation
- 角速度矢量^ωθ 在参考坐标系{s}中描述,某坐标系初始与参考坐标系{s}重合,以角速度^ωθ转动,经过单位时间到达当前姿态(可由矩阵R表示)。
- 角速度矢量^ω在参考坐标系{s}中描述,某坐标系初始与参考坐标系{s}重合,以角速度^ω转动,经过θ时间到达当前姿态(可由矩阵R表示)。
- Essential Results from Linear Differential Equations Theory
考虑下面的一阶线性微分方程:˙x(t)=Ax(t)
其中,x(t)∈Rn,A∈Rn×n是一个常量矩阵。若给出初始条件x(0)=x0,则可得到微分方程的解为:x(t)=x0eAt
矩阵指数eAt可以根据泰勒展开式来计算:eAt=I+At+(At)22!+(At)33!+...
如果矩阵A可以表达成A=PDP−1,P为可逆矩阵,则有:
eAt=I+At+(At)22!+(At)33!+...=I+(PDP−1)t+(PDP−1)(PDP−1)t22!+...=P(I+Dt+(Dt)22!+...)P−1=PeDtP−1
更进一步,如果A可以对角化,即D是对角矩阵:D=diag{d1,d2,...,dn},则eDt可以很方便的计算:
eDt=⎡⎢
⎢
⎢
⎢
⎢⎣ed1t0⋯00ed2t⋯0⋮⋮⋱⋮00⋯ednt⎤⎥
⎥
⎥
⎥
⎥⎦
- Exponential Coordinates of Rotations
参考下图中的描述,假设三维向量p(0)绕着转轴^ω旋转θ度后到达p(θ)。用p(t)代表t时刻向量p的位置,则该过程也可以描述为:p(0)以角速度^ω旋转(^ω为单位角速度),从t=0运动到t=θ。
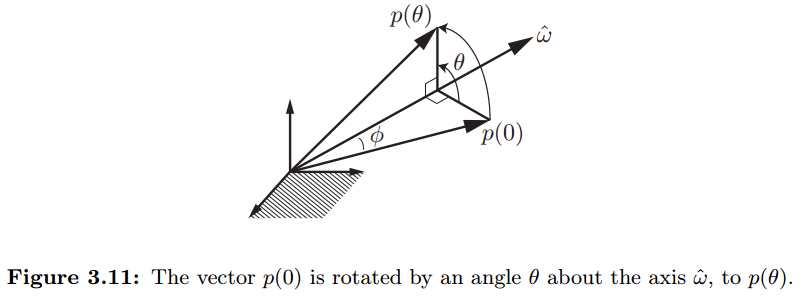
旋转时的速度可用˙p来描述,且有:˙p=^ω×p
用斜对称矩阵[^ω]可以将向量叉乘变为矩阵与向量乘法,因此上面的微分方程可写为:˙p=[^ω]p
若^ω=[ωx,ωy,ωz]T,定义斜对称矩阵[^ω]:
[^ω]=⎡⎢⎣0−ωzωyωz0−ωx−ωyωx0⎤⎥⎦
已知初始条件p(0),该方程形式如前面研究过的˙x=Ax,因此其解为:p(t)=e[^ω]tp(0)
由于变量t和θ可互换,则上面方程可写为:p(θ)=e[^ω]θp(0)
下面将e[^ω]t进行泰勒展开,计算斜对称矩阵[^ω]的幂可得关系式:[^ω]3=−[^ω],利用这一关系我们可以将[^ω]3替换为−[^ω],[^ω]4替换为−[^ω]2,[^ω]5替换为−[^ω]3...于是可以得到:
e[^ω]θ=I+[^ω]θ+[^ω]2θ22!+[^ω]3θ33!+...=I+(θ−θ33!+θ55!−...)[^ω]+(θ22!−θ44!−θ66!−...)[^ω]2
根据正弦和余弦函数的泰勒展开式:
sinθ=θ−θ33!+θ55!−...cosθ=1−θ22!+θ44!−...
可以将上面公式进行简化。给定^ωθ∈R3,其中θ为任意标量,^ω∈R3且为单位向量。则根据[^ω]、θ进行旋转的旋转矩阵为:Rot(^ω,θ)=e[^ω]θ=I+sinθ[^ω]+(1−cosθ)[^ω]2
该公式也称为Rodrigues’ formula(罗德里格斯公式) 。
举个例子,下图中坐标系{b}相对于固定参考坐标系{s}的姿态可以描述为:初始时刻两坐标系一致,{b}绕单位向量^ω1=(0,0.866,0.5)旋转θ1=30∘=0.524rad后到达当前姿态。
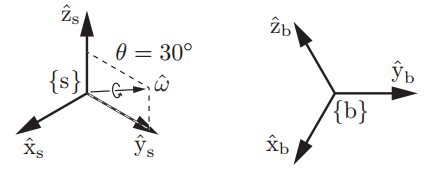
则{b}相对于{s}的旋转矩阵可以计算为:
R=e[^ω1]θ1=I+sinθ1[^ω1]+(1−cosθ1)[^ω1]2=I+0.5⎡⎢⎣0−0.50.8660.500−0.86600⎤⎥⎦+0.134⎡⎢⎣0−0.50.8660.500−0.86600⎤⎥⎦2=⎡⎢⎣0.866−0.2500.4330.2500.9670.058−0.4330.0580.899⎤⎥⎦
坐标系{b}的姿态可由矩阵R描述,或者由单位向量^ω1=(0,0.866,0.5)以及转角θ1=0.524rad来描述,即旋转矩阵R的指数坐标为^ω1θ1=(0,0.453,0.262)
在Mathematica中RotationMatrix函数可以根据转轴和转角计算旋转矩阵:

- Matrix Logarithm of Rotations
如果向量^ωθ∈R3表达了旋转矩阵R的指数坐标,则斜对称矩阵[^ωθ]=[^ω]θ是旋转矩阵R的对数。矩阵的对数是矩阵指数的逆:
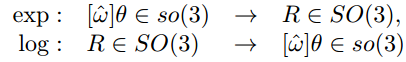
当转角θ不为π的整数倍时,可以根据旋转矩阵R计算出转轴:^ωx=12sinθ(r32−r23)^ωy=12sinθ(r13−r31)^ωz=12sinθ(r21−r12)
或表述为斜对称矩阵形式:[^ω]=⎡⎢⎣0−^ωz^ωy^ωz0−^ωx−^ωy^ωx0⎤⎥⎦=12sinθ(R−RT)
具体推导和细节可参考:Modern Robotics: Mechanics, Planning, and Control 3.2.3.3 Matrix Logarithm of Rotations
参考:
物理引擎中的刚体转动2
四元数指数映射旋转参数化的实际应用
视觉SLAM中的数学基础 第二篇 四元数
视觉SLAM中的数学基础 第三篇 李群与李代数
李群与李代数 - part 2 指数与对数映射、李代数求导与扰动模型
Axis–angle representation
Rodrigues' rotation formula
Lie Groups for 2D and 3D Transformations
Modern Robotics: Mechanics, Planning, and Control 3.2.3 Exponential Coordinate Representation of Rotation
Lie groups, Lie algebras, projective geometry and optimization for 3D Geometry, Engineering and Computer Vision

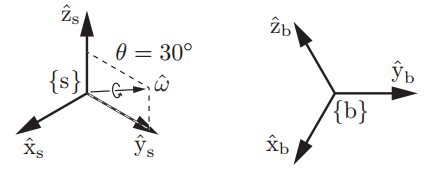

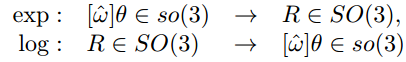





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律