物理引擎中的刚体转动2

旋转矩阵R的微分

　　对于线性位移$x(t)$和线性速度$v(t)$，很容易得出$v(t)=\frac{d}{dt}x(t)$。那么旋转矩阵$R(t)$和角速度$\omega(t)$之间的关系是怎样的呢？显然$\dot{R}(t)$不等于$\omega(t)$，因为$R(t)$是一个矩阵，而$\omega(t)$是向量。为了回答这个问题，回忆一下矩阵$R(t)$的实际意义。我们知道$R(t)$的列向量就是其坐标系在世界坐标系中的方向向量，因此$\dot{R}(t)$的列向量描述了刚体旋转时$x$，$y$，$z$轴的“速度”。下图描述了一个刚体以角速度$\omega(t)$进行旋转，考虑刚体上某一位置向量$r(t)$，其速度很容易推导出为：$$\dot{r}(t)=\omega(t) \times r(t)$$

　　$t$时刻，刚体$x$轴的方向向量在世界坐标系下的坐标为矩阵$R(t)$的第一列：$(r_{xx},r_{xy},r_{xz})^T$，则在$t$时刻$R(t)$第一列的微分就是该向量的变化率。根据上面的推论，我们可得到该微分为：$\omega(t) \times (r_{xx},r_{xy},r_{xz})^T$　　

　　对$R(t)$的另外两个列向量情况也一样。因此，我们可以写出：

$$\dot{R(t)}=\begin{pmatrix}
\omega(t) \times\begin{pmatrix} r_{xx}\\ r_{xy}\\ r_{xz} \end{pmatrix}
& \omega(t) \times\begin{pmatrix} r_{yx}\\ r_{yy}\\ r_{yz} \end{pmatrix}
& \omega(t) \times\begin{pmatrix} r_{zx}\\ r_{zy}\\ r_{zz} \end{pmatrix}
\end{pmatrix}$$

　　根据角速度$\omega$定义斜对称矩阵（skew-symmetric matrix）$\Omega$，斜对称矩阵满足$\Omega^T=-\Omega$：

$$\Omega=\begin{pmatrix}
0 & -\omega_z & \omega_y\\
\omega_z & 0 & -\omega_x\\
-\omega_y & \omega_x & 0
\end{pmatrix}$$

　　可以证明，对任意向量$P$均有：$$\omega \times P = \Omega P$$

　　则旋转矩阵$R(t)$的微分可以用角速度的斜对称矩阵表示为：$$\dot{R}(t)=\Omega R(t)$$

惯性参考系中的Euler方程

　　通常Euler方程中各量均为在与刚体固连的坐标系中表达，但这并不意味着此方程只在与刚体固连的坐标系中才成立。事实上很容易证明：对任一坐标系均有$$I \dot{\omega}+\omega \times I \omega =N$$

　　式中各量均为在上述给定坐标系中的表达式。当然，将Euler方程表示在与刚体固连坐标系中尤其特殊的优点，即惯性张量矩阵是常值矩阵，它可以预先计算或辨识出来，这给Euler方程的应用带来很大方便。如果欧拉方程在惯性坐标系中描述，那么惯性张量是个随着刚体运动而变化的变量，需要实时计算该值。

　　下面从动量矩定理开始推导惯性坐标系下的欧拉方程。等式中物理量下标$I$表示该量在惯性参考系（Inertia frame）中描述，这里刚体的惯性张量$I$不再恒定，而是随时间变化的量，因此在求导时要注意：

$$\boldsymbol\tau_I = \frac d{dt} (\mathrm I_I\, \boldsymbol \omega_I) =
\mathrm I_I \, \dot {\boldsymbol \omega}_I
+ \dot {\mathrm I}_I \,\boldsymbol \omega_I$$

　　惯性参考系下的惯性张量$I_I$和刚体局部参考系下的惯性张量$I_b$（$I_b$是常量）之间的关系如下：$$I_I=RI_bR^T$$

　　其中，矩阵$R$是刚体局部坐标系相对于惯性坐标系（世界坐标系）的变换，即$^I_bR$。考虑惯性张量$I_I$对时间的导数：$\dot{I}_I=\dot{R}I_bR^T+RI_b \dot{R}^T$

　　变换矩阵$R$的导数可以表示为：$\dot{R}=Sk(\omega_I)R$，$Sk(\omega_I)$是根据角速度$\omega_I$构造的斜对称矩阵。则有：$\dot{I}_I=Sk(\omega_I)RI_bR^T+RI_bR^TSk^T(\omega_I)=Sk(\omega_I)I_I-I_ISk(\omega_I)$

　　于是$\dot{I}_I\omega_I=Sk(\omega_I)I_I\omega_I-I_ISk(\omega_I)\omega_I=\omega_I \times (I_I\omega_I)-I_I(\omega_I \times \omega_I)=\omega_I \times (I_I\omega_I)$

　　因此，惯性参考系中的欧拉公式为：

$$\boldsymbol\tau_I =
\mathrm I_I \, \dot {\boldsymbol \omega}_I
+ \boldsymbol \omega_I \times (\mathrm I_I \,\boldsymbol \omega_I)$$

　　可以看出，惯性参考系下欧拉公式与刚体局部坐标系下欧拉公式形式一致，只是物理量的参照基准不同。

陀螺力矩

　　欧拉方程$I \dot{\omega}+\omega \times I\omega=\tau$中的$\omega \times I\omega$项在物理引擎中被称为陀螺力矩（gyroscopic torque），因为其有力矩的量纲。陀螺力矩的产生是由于角速度与角动量方向不一致，$\omega \times I\omega$叉乘结果不为零。

　　在某些游戏物理引擎中为了避免复杂计算影响实时性和稳定性，通常会忽略陀螺力矩，即直接使用公式：$$I\dot{\omega}=\tau$$

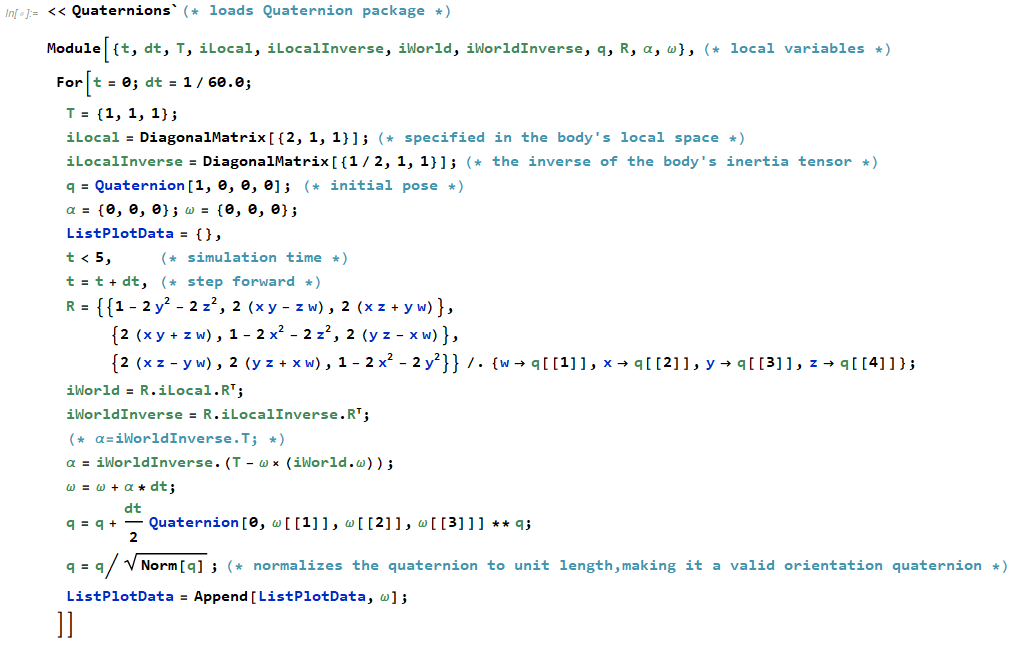
　　那么对于物理引擎中的刚体转动1中描述的那个问题，添加$\omega \times I\omega$项后准确的计算如下面Mathematica代码所示：

　　画出结果，可以发现与bullet2.83、ODE物理引擎中模拟的结果一致（仿真时间设为5s）：

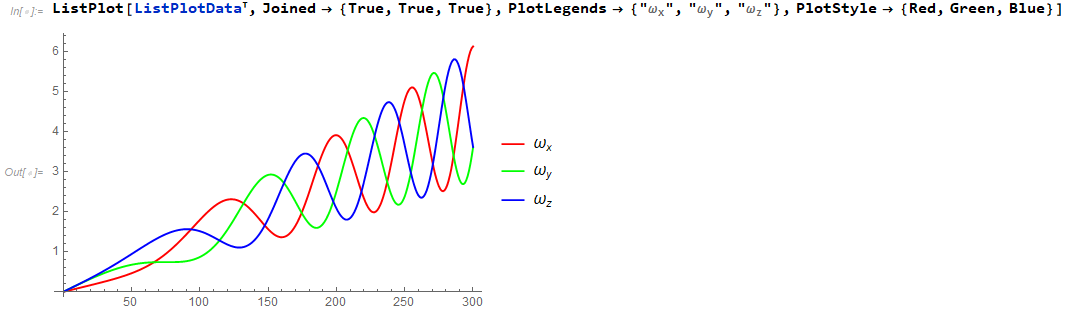
　　bullet物理引擎从2.83版本开始才默认开启了陀螺力矩的计算。

// bullet 2.83
enum    btRigidBodyFlags
{
    BT_DISABLE_WORLD_GRAVITY = 1,
    ///BT_ENABLE_GYROPSCOPIC_FORCE flags is enabled by default in Bullet 2.83 and onwards.
    ///and it BT_ENABLE_GYROPSCOPIC_FORCE becomes equivalent to BT_ENABLE_GYROSCOPIC_FORCE_IMPLICIT_BODY
    ///See Demos/GyroscopicDemo and computeGyroscopicImpulseImplicit
    BT_ENABLE_GYROSCOPIC_FORCE_EXPLICIT = 2,
    BT_ENABLE_GYROSCOPIC_FORCE_IMPLICIT_WORLD=4,
    BT_ENABLE_GYROSCOPIC_FORCE_IMPLICIT_BODY=8,
    BT_ENABLE_GYROPSCOPIC_FORCE = BT_ENABLE_GYROSCOPIC_FORCE_IMPLICIT_BODY,
};



// bullet 2.82
enum    btRigidBodyFlags
{
    BT_DISABLE_WORLD_GRAVITY = 1,
    ///The BT_ENABLE_GYROPSCOPIC_FORCE can easily introduce instability
    ///So generally it is best to not enable it. 
    ///If really needed, run at a high frequency like 1000 Hertz:    ///See Demos/GyroscopicDemo for an example use
    BT_ENABLE_GYROPSCOPIC_FORCE = 2
};

View Code

　　bullet2.83中与陀螺力矩相关的计算如下面代码所示：

// 四元数与向量乘法运算符重载
btQuaternion operator*(const btQuaternion& q, const btVector3& w)
{
    return btQuaternion( 
         q.w() * w.x() + q.y() * w.z() - q.z() * w.y(),
         q.w() * w.y() + q.z() * w.x() - q.x() * w.z(),
         q.w() * w.z() + q.x() * w.y() - q.y() * w.x(),
        -q.x() * w.x() - q.y() * w.y() - q.z() * w.z()); 
}


// 用四元数旋转向量
btVector3 quatRotate(const btQuaternion& rotation, const btVector3& v) 
{
    btQuaternion q = rotation * v;
    q *= rotation.inverse();
    return btVector3(q.getX(),q.getY(),q.getZ());
}


// 对单位四元数来说其逆等于其共轭四元数
btQuaternion inverse() const
{
    return btQuaternion(-m_floats[0], -m_floats[1], -m_floats[2], m_floats[3]);
}


void getSkewSymmetricMatrix(btVector3* v0,btVector3* v1,btVector3* v2) const
{
    v0->setValue(0.        ,-z()        ,y());
    v1->setValue(z()    ,0.            ,-x());
    v2->setValue(-y()    ,x()    ,0.);
}
    

/// Solve A * x = b, where b is a column vector. This is more efficient
/// than computing the inverse in one-shot cases.
///Solve33 is from Box2d, thanks to Erin Catto,
btVector3 solve33(const btVector3& b) const
{
    btVector3 col1 = getColumn(0);
    btVector3 col2 = getColumn(1);
    btVector3 col3 = getColumn(2);
    
    btScalar det = btDot(col1, btCross(col2, col3));
    if (btFabs(det)>SIMD_EPSILON) 
    {
        det = 1.0f / det;  // 如果方程组系数行列式不等于零，则方程组有唯一解
    }
    btVector3 x;
    x[0] = det * btDot(b, btCross(col2, col3));  // 参考《线性代数》克拉默法则
    x[1] = det * btDot(col1, btCross(b, col3));
    x[2] = det * btDot(col1, btCross(col2, b));
    return x;
}
    
    
btVector3 btRigidBody::computeGyroscopicImpulseImplicit_Body(btScalar step) const
{    
    btVector3 idl = getLocalInertia(); 
    btVector3 omega1 = getAngularVelocity();  // angular velocity expressed in inertia frame
    btQuaternion q = getWorldTransform().getRotation();  
    
    // Convert to body coordinates
    btVector3 omegab = quatRotate(q.inverse(), omega1);
    
    // Inertia tensor expressed in local frame
    btMatrix3x3 Ib;
    Ib.setValue(idl.x(),0,0,
                0,idl.y(),0,
                0,0,idl.z());
    
    btVector3 ibo = Ib*omegab;  // Iw

    // Residual vector
    btVector3 f = step * omegab.cross(ibo);  // f = dt· w×(Iw)
    
    btMatrix3x3 skew0;
    omegab.getSkewSymmetricMatrix(&skew0[0], &skew0[1], &skew0[2]);
    
    btVector3 om = Ib*omegab;
    btMatrix3x3 skew1;
    om.getSkewSymmetricMatrix(&skew1[0],&skew1[1],&skew1[2]);
    
    // Jacobian
    btMatrix3x3 J = Ib +  (skew0*Ib - skew1)*step;
    
//    btMatrix3x3 Jinv = J.inverse();
//    btVector3 omega_div = Jinv*f;
    btVector3 omega_div = J.solve33(f);
    
    // Single Newton-Raphson update
    omegab = omegab - omega_div;//Solve33(J, f);
    // Back to world coordinates
    btVector3 omega2 = quatRotate(q,omegab);
    btVector3 gf = omega2-omega1;
    return gf;
}


btVector3 btRigidBody::computeGyroscopicImpulseImplicit_World(btScalar step) const
{
    // use full newton-euler equations.  common practice to drop the wxIw term. want it for better tumbling behavior.
    // calculate using implicit euler step so it's stable.

    const btVector3 inertiaLocal = getLocalInertia();
    const btVector3 w0 = getAngularVelocity();

    btMatrix3x3 I;

    I = m_worldTransform.getBasis().scaled(inertiaLocal) *
        m_worldTransform.getBasis().transpose();  // I_world

    // use newtons method to find implicit solution for new angular velocity (w')
    // f(w') = -(T*step + Iw) + Iw' + w' + w'xIw'*step = 0 
    // df/dw' = I + 1xIw'*step + w'xI*step

    btVector3 w1 = w0;

    // one step of newton's method
    {
        const btVector3 fw = evalEulerEqn(w1, w0, btVector3(0, 0, 0), step, I);
        const btMatrix3x3 dfw = evalEulerEqnDeriv(w1, w0, step, I);

        btVector3 dw;
        dw = dfw.solve33(fw);
        //const btMatrix3x3 dfw_inv = dfw.inverse();
        //dw = dfw_inv*fw;

        w1 -= dw;
    }

    btVector3 gf = (w1 - w0);
    return gf;
}

View Code

注意以下几点：

　　1. 用四元数对向量进行旋转变换（参考quaternion）。The components a vector can be transformed between any two different reference frame orientations using the following formula:$$V_B=Q\otimes V_A\otimes Q^*$$ where,

V_A = vector (pure quaternion) in Frame A coordinates

V_B = vector (pure quaternion) in Frame B coordinates

Q = normalized quaternion for orientation of Frame B relative to Frame A.

Q* = conjugate (or inverse) of Q

= quaternion product

　　2. bullet2.83在btSequentialImpulseConstraintSolver约束求解器中求解约束，并更新速度（注意与之前版本的区别）。角速度更新主要应用了冲量矩(moment of impulse)/角冲量(angular impulse)定理。主要有以下3步：

// 根据冲量矩定理计算角动量的变化。这里乘了逆惯性张量，得出的是dt时间段内角速度的变化量
// 计算外力矩引起的角速度变化。m_externalTorqueImpulse实际是角速度变化量
solverBody->m_externalTorqueImpulse = rb->getTotalTorque()*rb->getInvInertiaTensorWorld()*timeStep ;

// 计算陀螺力矩引起的角速度变化并将其加到m_externalTorqueImpulse上
gyroForce = body->computeGyroscopicImpulseImplicit_Body(infoGlobal.m_timeStep); // gyroForce实际是角速度变化量
solverBody.m_externalTorqueImpulse += gyroForce;

// 更新刚体角速度
m_tmpSolverBodyPool[i].m_originalBody->setAngularVelocity(
        m_tmpSolverBodyPool[i].m_angularVelocity + m_tmpSolverBodyPool[i].m_externalTorqueImpulse);

View Code

　3. 陀螺力矩的计算原理。

　　根据欧拉方程很容易得到$\Delta\omega=\omega_2-\omega_1=\Delta tI^{-1}(T-\omega_1 \times I\omega_1)$，其中$\omega_1$是前一步的角速度、$\omega_2$是下一步的角速度。但是直接使用该公式迭代计算结果很容易发散。例如将上面Mathematica代码中的仿真时间延长（设为50s），时间步长分别设为1/30和1/60，运行结果如下左右两幅图所示：

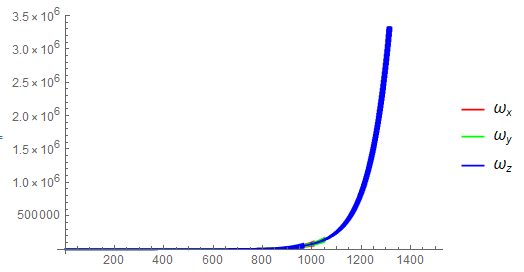
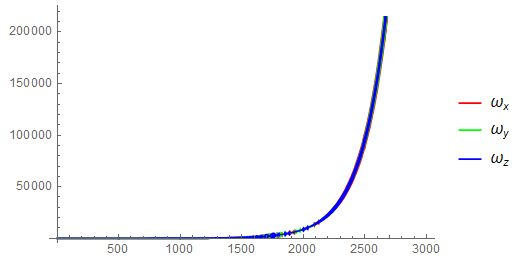
　　下面是专业多体动力学软件SIMPACK中的结果，对比可以看出上面的计算明显发散了（为了增加计算稳定性可以减小时间步长，但这么做的代价很大）。

　　关于仿真稳定性方面的问题可以参考：前向后项差分和显式隐式欧拉法、数值天气预报、布料仿真中常用积分方法、用数值模拟行星运动，很难得到稳定解？

　　Bullet2.83中使用下面的方法（参考Numerical Methods_Erin Catto）：

stage 1 explicit（显式计算外力矩引起的角速度变化）：$\Delta\omega_1=\Delta tI^{-1}T$
stage 2 implicit（隐式计算陀螺力矩引起的角速度变化）：$\Delta\omega_2=-\Delta tI^{-1}(\omega_2\times I\omega_2)$

　　于是有：$\omega_2=\omega_1+\Delta \omega_1+\Delta\omega_2$

　　对于stage1可以根据上一步的角速度用公式直接计算出下一步角速度，这种方法是显式的；而stage2中公式的右端包含有未知的下一步角速度，它实际上是关于下一步角速度的一个函数方程，这种方法是隐式的。考虑到数值稳定性等因素，有时需要选用隐式方法。隐式方程通常用迭代法求解，而迭代过程的实质是逐步显式化。

　　下面看看怎么隐式计算陀螺力矩引起的角速度的变化。不考虑外力矩，则欧拉方程可写为：$$F(\omega_2)=I(\omega_2-\omega_1)+\Delta t \omega_2 \times I\omega_2=0$$

　　需要注意的一点是上面方程中的惯性张量与角速度都应以同一个坐标系为参考。如果角速度相对世界坐标系描述，那么惯性张量$I$也应是在世界坐标系下描述；如果角速度相对刚体局部坐标系描述，那么惯性张量$I$也应是在刚体局部坐标系下描述。对应两种不同的坐标系bullet2.83中有两种不同的函数，分别为computeGyroscopicImpulseImplicit_World 和 computeGyroscopicImpulseImplicit_Body。在世界坐标系下计算需要将局部惯性张量转换到世界坐标系下，在局部坐标系下计算需要将世界坐标系中的角速度转换到局部坐标系下。bullet默认使用的是局部坐标系下的计算函数computeGyroscopicImpulseImplicit_Body。

　　求解该方程，即$F(\omega_2)=0$，即可解得$\omega_2$。这是一个非线性方程/组，可使用牛顿法（Newton-Raphson）进行求解。对多元非线性方程组$\mathbf{F(x)=0}$，$\mathbf{F(x)}$的雅可比矩阵$\mathbf{J=F'(x)}$。则非线性方程组的牛顿迭代法为：$$\mathbf{x^{(k+1)}=x^{(k)}-J^{-1}(x^{(k)})F(x^{(k)})}$$

　　牛顿迭代法在单根附近具有2阶收敛，在步长较小的情况下，迭代初始值与方程的根接近，能保证迭代快速收敛。这里每次迭代初始点都是上一步的角速度$\omega_1$，因此牛顿迭代公式中的$F(x^{(k)})=\Delta t \omega_1 \times I\omega_1$

　　$F(\omega_2)$的雅可比矩阵为：$J=\frac{d(I(\omega_2-\omega_1)+\Delta t \omega_2 \times I\omega_2)}{d\omega_2}=I+\Delta t \frac{d(\omega_2 \times I\omega_2)}{d\omega_2}$

　　其中：

$$\begin{align*}
d(\omega \times I\omega)&=\omega \times d(I\omega)+d\omega \times I\omega \\& = \omega \times Id\omega-I\omega\times d\omega \\&
=Skew(\omega)Id\omega-Skew(I\omega)d\omega
\end{align*}$$

　　于是有：$$\frac{d(\omega \times I\omega)}{d\omega}=Skew(\omega)I-Skew(I\omega)$$

　　于是可得到函数$F$的雅可比矩阵为：$$J=I+\Delta t[Skew(\omega)I-Skew(I\omega)]$$

　　根据这些推论，将其带入迭代公式可以计算出下一步角速度，并输出角速度变化量。

　　4. 用角速度更新刚体姿态　　

　　根据动力学方程积分求得角速度后需要更新刚体姿态，在bullet中实际上用的是下面的方法（参考论文：Practical Parameterization of Rotations Using the Exponential Map）

static void integrateTransform(const btTransform& curTrans,const btVector3& linvel,const btVector3& angvel,btScalar timeStep,btTransform& predictedTransform)
{
    predictedTransform.setOrigin(curTrans.getOrigin() + linvel * timeStep);
//#define QUATERNION_DERIVATIVE
#ifdef QUATERNION_DERIVATIVE
    btQuaternion predictedOrn = curTrans.getRotation();
    predictedOrn += (angvel * predictedOrn) * (timeStep * btScalar(0.5));
    predictedOrn.normalize();
#else
    //Exponential map
    //google for "Practical Parameterization of Rotations Using the Exponential Map", F. Sebastian Grassia

    btVector3 axis;
    btScalar    fAngle = angvel.length(); 
    //limit the angular motion
    if (fAngle*timeStep > ANGULAR_MOTION_THRESHOLD)
    {
        fAngle = ANGULAR_MOTION_THRESHOLD / timeStep;
    }

    if ( fAngle < btScalar(0.001) )
    {
        // use Taylor's expansions of sync function
        axis   = angvel*( btScalar(0.5)*timeStep-(timeStep*timeStep*timeStep)*(btScalar(0.020833333333))*fAngle*fAngle );
    }
    else
    {
        // sync(fAngle) = sin(c*fAngle)/t
        axis   = angvel*( btSin(btScalar(0.5)*fAngle*timeStep)/fAngle );
    }
    btQuaternion dorn (axis.x(),axis.y(),axis.z(),btCos( fAngle*timeStep*btScalar(0.5) ));
    btQuaternion orn0 = curTrans.getRotation();

    btQuaternion predictedOrn = dorn * orn0;
    predictedOrn.normalize();
#endif
    predictedTransform.setRotation(predictedOrn);
}

View Code

　　旋转$\mathbf{q}$可由三维向量$\pmb{\omega}\in\mathbb{R^3}$来表示。向量幅值代表绕其旋转的角度，单位向量$\pmb{\hat{\omega}}$表示旋转轴的方向。对向量$\pmb{\omega}$进行单位化：$\pmb{\hat{\omega}}=\pmb{\omega}/|\pmb{\omega}|$，当其幅值很小接近零时容易引起计算不稳定。四元数$\mathbf{q}$可写为：$$\mathbf{q}=[\sin(\theta/2)\frac{\pmb{\omega}}{|\pmb{\omega}|},\cos(\theta/2)]^T$$

　　为了避免计算$\frac{\pmb{\omega}}{|\pmb{\omega}|}$时不稳定，将$\sin(\theta/2)$进行泰勒展开，则有：$\sin(\theta/2)=\frac{\theta}{2}-\frac{\theta^3}{48}+\frac{\theta^5}{3840}-...$

　　当$\theta$足够小时，使用上面计算公式的前两项来近似，即：$$\sin\frac{\theta}{2}=\frac{\theta}{2}-\frac{\theta^3}{48}$$

　　反之当$\theta$大小超过一定阈值时可以直接计算。

　　根据：$$\begin{align*} q(t+\Delta t)&=\Delta q* q(t)\\&=(\cos\frac{\Delta \theta}{2}+\pmb{\hat{\omega}}\sin\frac{\Delta \theta}{2})q(t) \end{align*}$$

　　将$\Delta\theta=\left |\omega\right |\Delta t$带入上面公式，即可求得刚体的新姿态$ q(t+\Delta t)$

稳定性、精度及优化问题

　　用牛顿第二定律（动量矩定理）解决物理问题，实际上是求解一个二阶常微分方程的问题。用数值方法进行刚体动力学模拟时，会涉及数值稳定性、求解精度等一系列问题。游戏物理引擎中对速度和位移进行积分时，通常用的都是欧拉法（Euler Integrator）、半隐式欧拉法（Semi-implicit Euler / Simplectic Euler）或隐式欧拉法（Implicit Euler method / Backward Euler method），除此之外还有龙格库塔法（Runge Kutta）、Verlet integration等方法，可以参考Numerical methods for ordinary differential equations。不同方法的求解精度、收敛性和计算速度都不一样，因此要根据需求选择合适的方法。

Numerical methods for integration
First-order methods	Euler method Backward Euler Semi-implicit Euler Exponential Euler
Second-order methods	Verlet integration Velocity Verlet Trapezoidal rule Beeman's algorithm Midpoint method Heun's method Newmark-beta method Leapfrog integration
Higher-order methods	Exponential integrators Runge–Kutta methods List of Runge–Kutta methods Linear multistep method General linear methods Backward differentiation formula Yoshida
Theory	Symplectic integrator