计算模糊控制离线查询表
- 论域为离散时模糊控制的离线计算
当论域为离散时，经过量化后的输入量的个数是有限的。因此可以针对输入情况的不同组合离线计算出相应的控制量，从而组成一张控制表，实际控制时只要直接查这张控制表即可，在线运算量是很少的。这种离线计算、在线查表的模糊控制方法比较容易满足实时控制的要求。下图表示了这种模糊控制系统的结构。
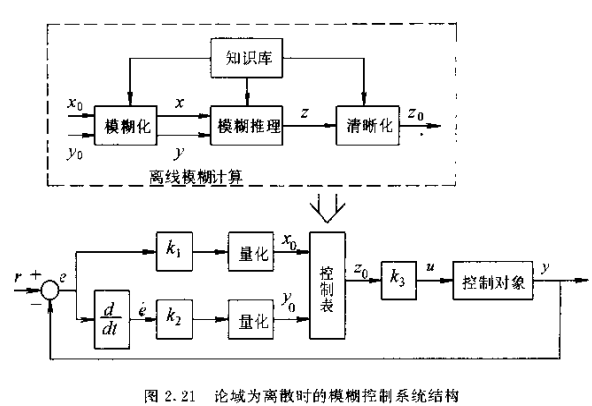
下面通过一个具体例子来说明离线模糊计算的过程。设X、Y、Z∈{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}，T(x)={NB,NM,NS,NZ,PZ,PS,PM,PB}，T(y)=T(z)={NB,NM,NS,ZE,PS,PM,PB}
语言变量x的隶属度函数如下表：
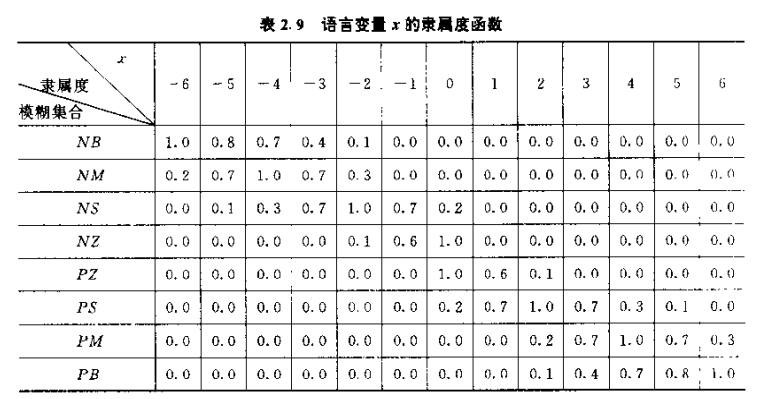
语言变量y和z的隶属度函数同下表：
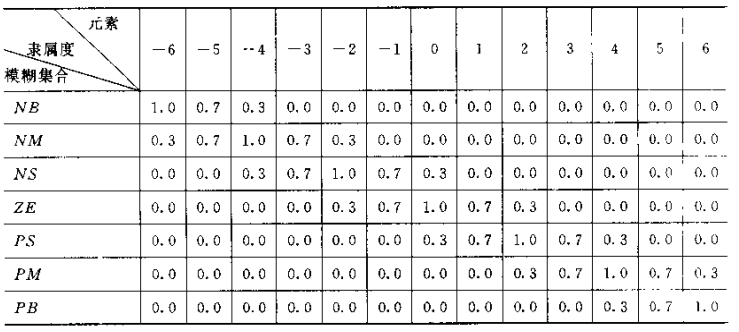
模糊控制规则如下表所示：
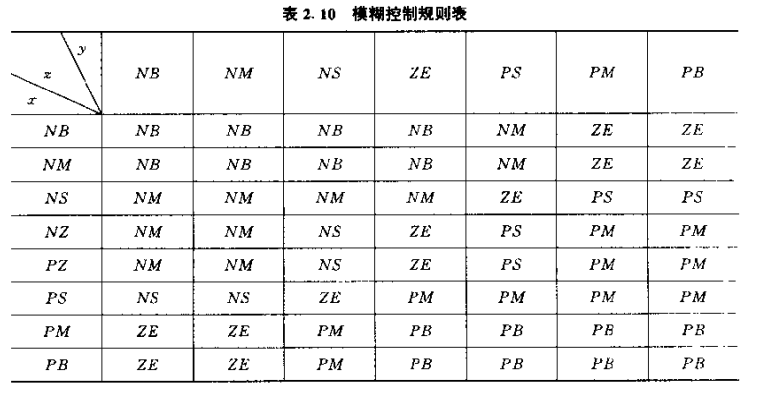
设已知输入为x0和y0，模糊化运算采用单点模糊集合，则相应的输入量模糊集合A'和B'分别为
$$\mu_{A'}(x)=\left\{\begin{matrix}
1 \quad x=x_0\\
0 \quad x\neq x_0
\end{matrix}\right. \quad
\mu_{B'}(y)=\left\{\begin{matrix}
1 \quad y=y_0\\
0 \quad y\neq y_0
\end{matrix}\right.$$
比如，假设x输入为-4，则输入的模糊集合为：$A'=\frac{0}{-6}+\frac{0}{-5}+\frac{1}{-4}+\frac{0}{-3}+...+\frac{0}{5}+\frac{0}{6}$
根据书中的模糊推理方法及性质，可求得输出量的模糊集合C'为（假设and用求交法，also用求并法，合成用最大—最小法，模糊蕴含用求交法）
$$\begin{align*}
C'&=(A' \times B')\circ R=(A' \times B')\circ \bigcup_{i=1}^{56} R_i\\
&=\bigcup_{i=1}^{56}(A' \times B')\circ [(A_i \times B_i)\rightarrow C_i]\\
&=\bigcup_{i=1}^{56}[A' \circ (A_i \rightarrow C_i)]\cap [B' \circ (B_i \rightarrow C_i)]\\
&=\bigcup_{i=1}^{56}C_{iA}' \cap C_{iB}'\\
&=\bigcup_{i=1}C_i'
\end{align*}$$
直接根据公式$C'=(A' \times B')\circ R=(A' \times B')\circ \bigcup_{i=1}^{56} R_i$计算输出C'的代码如下：
x=[1.0 0.8 0.7 0.4 0.1 0 0 0 0 0 0 0 0; % 语言变量x的隶属度函数,8*13
0.2 0.7 1.0 0.7 0.3 0 0 0 0 0 0 0 0;
0 0.1 0.3 0.7 1.0 0.7 0.2 0 0 0 0 0 0;
0 0 0 0 0.1 0.6 1.0 0 0 0 0 0 0;
0 0 0 0 0 0 1.0 0.6 0.1 0 0 0 0;
0 0 0 0 0 0 0.2 0.7 1.0 0.7 0.3 0.1 0;
0 0 0 0 0 0 0 0 0.2 0.7 1.0 0.7 0.3;
0 0 0 0 0 0 0 0 0.1 0.4 0.7 0.8 1.0];
y=[1.0 0.7 0.3 0 0 0 0 0 0 0 0 0 0; % 语言变量y和z的隶属度函数,7*13
0.3 0.7 1.0 0.7 0.3 0 0 0 0 0 0 0 0;
0 0 0.3 0.7 1.0 0.7 0.3 0 0 0 0 0 0;
0 0 0 0 0.3 0.7 1.0 0.7 0.3 0 0 0 0;
0 0 0 0 0 0 0.3 0.7 1.0 0.7 0.3 0 0;
0 0 0 0 0 0 0 0 0.3 0.7 1.0 0.7 0.3;
0 0 0 0 0 0 0 0 0 0 0.3 0.7 1.0];
z=y;
TABLE=[ 1 1 1 1 2 4 4;
1 1 1 1 2 4 4;
2 2 2 2 4 5 5;
2 2 3 4 5 6 6;
2 2 3 4 5 6 6;
3 3 4 6 6 6 6;
4 4 6 7 7 7 7;
4 4 6 7 7 7 7];% TABLE中元素为模糊控制规则表中每个元素在矩阵z中的行数
R_AB=zeros(13,13);
R_i=zeros(169,13);
R=zeros(169,13); % 模糊关系矩阵,169*13
for i=1:8 % 控制规则表x从NB—>PB
for j=1:7 % 控制规则表y从NB—>PB
A=x(i,:); % 取A为矩阵x的第i行
B=y(j,:); % 取B为矩阵y的第j行
Ur=TABLE(i,j); % x第i行和y的第j列对应的控制规则
C=z(Ur,:); % C为根据模糊控制规则推出结果对应的模糊集合
for m=1:13 % x的论域量化为13个等级-6~6
for n=1:13 % y的论域量化为13个等级-6~6
if A(m)<B(n)
R_AB(m,n)=A(m); % 取小运算
else
R_AB(m,n)=B(n);
end
end
end
R_AB1=reshape(R_AB',169,1); % 需要注意的是reshape是按列读取，然后按列摆放
for m=1:169
for n=1:13 % 矩阵R_i(m,n)为169行13列
if R_AB1(m)<C(n)
R_i(m,n)=R_AB1(m); % 取小运算
else
R_i(m,n)=C(n);
end
end
end
%*************求总的模糊关系矩阵*****************
for m=1:169
for n=1:13
if R(m,n)<R_i(m,n)
R(m,n)=R_i(m,n); % 模糊并运算，取大
end
end
end
end
end
%***************计算输出量的模糊集合*********************
OUTPUT = zeros(13,13);
for i=1:13
for j=1:13
A1=zeros(1,13); A1(i)=1; % 单点模糊集合A'
B1=zeros(1,13); B1(j)=1; % 单点模糊集合B'
for m=1:13
for n=1:13
if A1(m)<B1(n)
R_AB(m,n)=A1(m); %取小运算
else
R_AB(m,n)=B1(n);
end
end
end
R_AB1=reshape(R_AB',169,1);
U=zeros(1,13);
for m=1:13
for n=1:169
U(m)=max(min(R_AB1(n),R(n,m)),U(m)); %模糊关系矩阵的合成运算
end
end
%*********************重心法去模糊化********************************
temp = 0;
for m=1:13
temp = temp + U(m)* (m-7);
end
OUTPUT(i,j) = temp/sum(U);
end
end
当输入的维数较高，即有很多个模糊子句用and相连时，模糊推理的计算便比较复杂。根据模糊推理的性质(参考《智能控制理论与技术》第2版 2.5.4)，推导出新的计算公式，每个子模糊蕴含关系都比较简单，模糊矩阵的维数也较低，并不随着and连接的模糊子句的个数增加而增加。这种方式计算C'的MATLAB代码如下：
clc; % 清空命令窗口
clear; % 清空变量
x=[1.0 0.8 0.7 0.4 0.1 0 0 0 0 0 0 0 0; % 语言变量x的隶属度函数,8*13
0.2 0.7 1.0 0.7 0.3 0 0 0 0 0 0 0 0;
0 0.1 0.3 0.7 1.0 0.7 0.2 0 0 0 0 0 0;
0 0 0 0 0.1 0.6 1.0 0 0 0 0 0 0;
0 0 0 0 0 0 1.0 0.6 0.1 0 0 0 0;
0 0 0 0 0 0 0.2 0.7 1.0 0.7 0.3 0.1 0;
0 0 0 0 0 0 0 0 0.2 0.7 1.0 0.7 0.3;
0 0 0 0 0 0 0 0 0.1 0.4 0.7 0.8 1.0];
y=[1.0 0.7 0.3 0 0 0 0 0 0 0 0 0 0; % 语言变量y和z的隶属度函数,7*13
0.3 0.7 1.0 0.7 0.3 0 0 0 0 0 0 0 0;
0 0 0.3 0.7 1.0 0.7 0.3 0 0 0 0 0 0;
0 0 0 0 0.3 0.7 1.0 0.7 0.3 0 0 0 0;
0 0 0 0 0 0 0.3 0.7 1.0 0.7 0.3 0 0;
0 0 0 0 0 0 0 0 0.3 0.7 1.0 0.7 0.3;
0 0 0 0 0 0 0 0 0 0 0.3 0.7 1.0];
z=y;
TABLE=[ 1 1 1 1 2 4 4;
1 1 1 1 2 4 4;
2 2 2 2 4 5 5;
2 2 3 4 5 6 6;
2 2 3 4 5 6 6;
3 3 4 6 6 6 6;
4 4 6 7 7 7 7;
4 4 6 7 7 7 7];% TABLE中元素为模糊控制规则表中每个元素在矩阵z中的行数
R_iA=zeros(13,13);
R_iB=zeros(13,13);
Ci=zeros(1,13);
OUTPUT=zeros(13,13);
for xi=1:13 % 输入变量x的13个取值：-6~6
for yi=1:13 % 输入变量y的13个取值：-6~6
U=zeros(1,13);
for i=1:8 % 控制规则表x从NB—>PB
for j=1:7 % 控制规则表y从NB—>PB
A=x(i,:); % 取A为矩阵x的第i行
B=y(j,:); % 取B为矩阵y的第j行
Ur=TABLE(i,j); % x第i行和y的第j列对应的控制规则
C=z(Ur,:); % C为根据模糊控制规则推出结果对应的模糊集合
for m=1:13
for n=1:13
if A(m)<C(n)
R_iA(m,n)=A(m); % 取小运算(算A→C的蕴含关系)
else
R_iA(m,n)=C(n);
end
end
end
C_iA=zeros(1,13);
A=zeros(1,13); A(xi)=1; % 单点模糊集合A'
for m=1:13
for n=1:13
C_iA(m)=max(min(A(n),R_iA(n,m)),C_iA(m)); %模糊关系合成运算
end
end
%**********************************************************
for m=1:13
for n=1:13
if B(m)<C(n)
R_iB(m,n)=B(m); % 取小运算(算B→C的蕴含关系)
else
R_iB(m,n)=C(n);
end
end
end
C_iB=zeros(1,13);
B=zeros(1,13); B(yi)=1; % 单点模糊集合B'
for m=1:13
for n=1:13
C_iB(m)=max(min(B(n),R_iB(n,m)),C_iB(m)); %模糊关系合成运算
end
end
%**********************************************************
for m=1:13
Ci(m)=min(C_iA(m),C_iB(m));
end
for m=1:13
U(m)=max(Ci(m),U(m)); % 56条规则求并
end
end
end
%*********************重心法去模糊化********************************
temp = 0;
for m=1:13
temp = temp + U(m)* (m-7);
end
OUTPUT(xi,yi) = temp/sum(U);
end
end
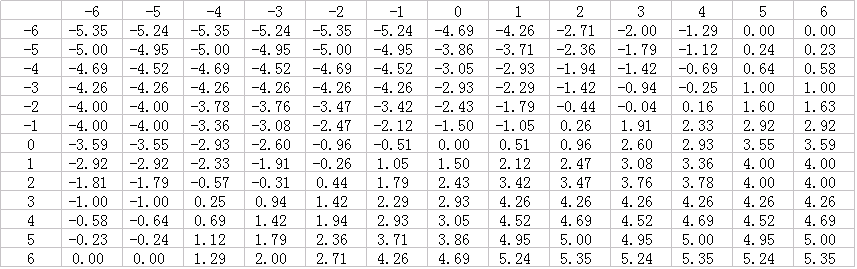
最终的模糊控制查询表如下：
参考：
