orocos_kdl学习（一）：坐标系变换
KDL中提供了点(point)、坐标系(frame)、刚体速度(twist)，以及6维力/力矩(wrench)等基本几何元素，具体可以参考 Geometric primitives 文档。
Creating a Frame, Vector and Rotation
PyKDL中创建一个坐标系时有下面4种构造函数：
__init__() # Construct an identity frame __init__(rot, pos) # Construct a frame from a rotation and a vector # Parameters: # pos (Vector) – the position of the frame origin # rot (Rotation) – the rotation of the frame __init__(pos) # Construct a frame from a vector, with identity rotation # Parameters: # pos (Vector) – the position of the frame origin __init__(rot) # Construct a frame from a rotation, with origin at 0, 0, 0 # Parameters: # rot (Rotation) – the rotation of the frame
下面是一个例子：
#! /usr/bin/env python import PyKDL # create a vector which describes both a 3D vector and a 3D point in space v = PyKDL.Vector(1,3,5) # create a rotation from Roll Pitch, Yaw angles r1 = PyKDL.Rotation.RPY(1.2, 3.4, 0) # create a rotation from ZYX Euler angles r2 = PyKDL.Rotation.EulerZYX(0, 1, 0) # create a rotation from a rotation matrix r3 = PyKDL.Rotation(1,0,0, 0,1,0, 0,0,1) # create a frame from a vector and a rotation f = PyKDL.Frame(r2, v) print f
结果将如下所示，前9个元素为代表坐标系姿态的旋转矩阵，后三个元素为坐标系f的原点在参考坐标系中的坐标。
[[ 0.540302, 0, 0.841471;
0, 1, 0;
-0.841471, 0, 0.540302]
[ 1, 3, 5]]
根据机器人学导论（Introduction to Robotics Mechanics and Control）附录中的12种欧拉角表示方法，ZYX欧拉角代表的旋转矩阵为：
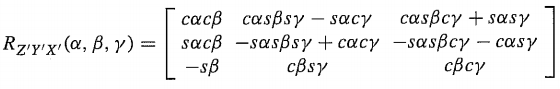
代入数据验证，KDL的计算与理论一致。
Extracting information from a Frame, Vector and Rotation
PyKDL中坐标系类Frame的成员M为其旋转矩阵，p为其原点坐标。
#! /usr/bin/env python import PyKDL # frame f = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0), PyKDL.Vector(3,2,4)) # get the origin (a Vector) of the frame origin = f.p # get the x component of the origin x = origin.x() x = origin[0] print x # get the rotation of the frame rot = f.M print rot # get ZYX Euler angles from the rotation [Rz, Ry, Rx] = rot.GetEulerZYX() print Rz,Ry,Rx # get the RPY (fixed axis) from the rotation [R, P, Y] = rot.GetRPY() print R,P,Y
将上述获取到的数据打印出来，结果如下：
3.0
[ 0.540302, 0, 0.841471;
0, 1, 0;
-0.841471, 0, 0.540302]
0.0 1.0 0.0
0.0 1.0 0.0
注意GetEulerZYX和GetRPY的结果是一样的，这其实不是巧合。因为坐标系的旋转有24种方式（本质上只有12种结果）：绕自身坐标系旋转有12种方式（欧拉角），绕固定参考坐标系旋转也有12种方式（RPY就是其中一种）。EulerZYX按照Z→Y→X的顺序绕自身坐标轴分别旋转$\alpha$、$\beta$、$\gamma$角；RPY按照X→Y→Z的顺序绕固定坐标系旋转$\gamma$、$\beta$、$\alpha$角，这两种方式最后得到的旋转矩阵是一样的。
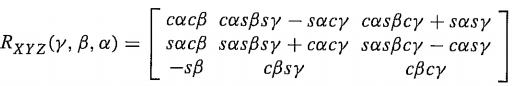
Transforming a point
frame既可以用来描述一个坐标系的位置和姿态，也可以用于变换。下面创建了一个frame，然后用其对一个空间向量或点进行坐标变换：
#! /usr/bin/env python import PyKDL # define a frame f = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0), PyKDL.Vector(3,2,4)) # define a point p = PyKDL.Vector(1, 0, 0) print p # transform this point with f p = f * p print p
Creating from ROS types
tf_conversions这个package包含了一系列转换函数，用于将tf类型的数据(point, vector, pose, etc) 转换为与其它库同类型的数据，比如KDL和Eigen。用下面的命令在catkin_ws/src中创建一个测试包：
catkin_create_pkg test rospy tf geometry_msgs
test.py程序如下（注意修改权限chmod +x test.py）：
#! /usr/bin/env python import rospy import PyKDL from tf_conversions import posemath from geometry_msgs.msg import Pose # you have a Pose message pose = Pose() pose.position.x = 1 pose.position.y = 1 pose.position.z = 1 pose.orientation.x = pose.orientation.y = pose.orientation.z = 0 pose.orientation.w = 1 # convert the pose into a kdl frame f1 = posemath.fromMsg(pose) # create another kdl frame f2 = PyKDL.Frame(PyKDL.Rotation.RPY(0,1,0), PyKDL.Vector(3,2,4)) # Combine the two frames f = f1 * f2 print f [x, y, z, w] = f.M.GetQuaternion() print x,y,z,w # and convert the result back to a pose message pose = posemath.toMsg(f) pub = rospy.Publisher('pose', Pose, queue_size=1) rospy.init_node('test', anonymous=True) rate = rospy.Rate(1) # 1hz while not rospy.is_shutdown(): pub.publish(pose) rate.sleep()
通过posemath.toMsg可以将KDL中的frame转换为geometry_msgs/Pose类型的消息。最后为了验证，创建了一个Publisher将这个消息发布到pose话题上。使用catkin_make编译后运行结果如下：
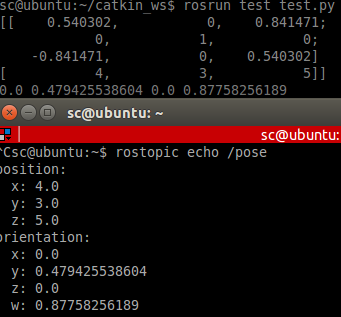
参考：
